环形振荡器电路延迟效应的研究与分析

李超然

（韩山师范学院计算机与信息工程学院，广东潮州 521041）

环形振荡器电路延迟效应的研究与分析

李超然

（韩山师范学院计算机与信息工程学院，广东潮州 521041）

环形振荡器是计算机硬件组成电路的重要组成部分，承载着信号输出和信号放大的作用.文章探寻环形振荡器电路延迟效应的成因，同时分析缩短这类电路延迟时间、提高电路运行效率的方法.在环形振荡器电路中，逆变器的电容量和尺寸是影响电路参数的两个关键因素.为了准确分析出这两个因素对振荡器电路中延迟参数的影响，文章通过保持固定数量的逆变器，来观察电路逆变器尺寸对电路延迟参数的影响；另一方面，通过固定逆变器的尺寸，来分析电路中逆变器数量对电路延迟参数的影响.通过这两个方面的测试，可以得出环形振荡器对电路延迟效应的影响.

环形振荡器；延迟参数；逆变器

1 引言

环形振荡器电路是由奇数个逆变器所组成的反馈系统.该电路含有奇数个串联的逆变器，最后一个逆变器必须与第一个逆变器形成反馈回路，从而使电路的输出电压通过反馈回路转化为电路的输入电压.

环形振荡器是利用门电路的固有传输延迟时间将奇数个反相器首尾相接而成，由于门电路的结构特性，在静态（假定没有振荡时）下任何一个反相器的输入和输出都不可能稳定在高电平或低电平状态，只能处于高、低电平之间，因此该电路不存在稳定状态[1].由于单个逆变器的计算逻辑为非门形式，奇数个的数量确保了末尾的逆变器计算的是首个逆变器的非门形式.该系统在运行过程中，最后一个信号将在第一个信号输入后的有限时间段内输出，并反馈回首个逆变器从而形成系统的新一个输入，这样的循环过程导致了电路不稳定的逻辑关系，形成了电路的环形回路振荡，这也是环形振荡器命名的由来.环形振荡器以其结构简单、起振难度小、便于集成化的优点被广泛应用，尤其是在数字电路的低频振荡中用途最广[2].这种振荡器的特点是线路简单，起振容易，如果不加延迟网络则不需要阻容元件，便于安放在集成电路系统中.然而，由于环形振荡器的主体部分由门电路的结构构成，门电路的延迟特性决定了环形振荡器电路存在一定的电路延迟现象，导致电路运行频率无法精确，进而使得系统无法控制电路的输出电压，造成系统传输信号的不稳定[3].因此，通过分析电路，从而深入探究系统延迟效应产生的根源并找出对应的解决办法，成为了降低延迟效应对环形振荡器电路性能的影响的一个重要方法.

2 环形振荡器的工作原理

最简易的环形振荡器是由3个逆变器串联而成的，称为三态环形振荡器，三态环形振荡器的工作过程是产生自激振荡的过程，其结构示意图如图1所示.

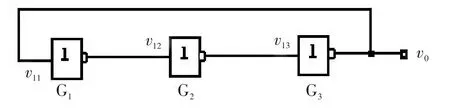
图1 三态环形振荡器的结构示意图

图2 三态环形振荡器的工作波形图

从图1可以看出，假定由于某种原因使第一个门G1的门电压v11产生了微小的正跳变，经G1的传输延迟时间t后，第二个门G2的门电压v12产生了一个幅度更大的负跳变，在经过G2的传输延迟时间t后，使第三个门G3的门电压v13产生更大的正跳变，经G3的传输延迟时间t后，在输出电压vo处产生一个更大的负跳变并反馈到第一个门G1的输入端.可见，在经过一共3t的时间段后，第一个门G1的门电压v11又自动跳变为低电平，再经过3t的时间段之后，第一个门G1的门电压v11又将跳变为高电平[4].如此周而复始，便产生自激振荡.三态振荡器电路工作的波形图如图2所示.从图2可以更加清晰地看出三态环形振荡器的电位变化，同时，也说明了振荡器电路具有振荡的周期性.环形振荡器是一个反馈电路，反馈的特性决定了其电路具有周期性，根据环形振荡器含有的逆变器的数量恒为奇数个的特性，可以得出：一个输入必须两次同步地流经整个电路才能再次得到该输入值，因此一个N阶环形振荡器应该有2N个循环周期，其周期系数T=2×2N即为4N.根据环形振荡器电路的周期性，可以得知在环形振荡器的波形图中，其波峰值频率应为一个周期的四分之一，即.设定一个逆变器的延迟时间为3 ps，可以得出一个N阶环形振荡器的电路频率F=1/（4×，单位为Hz[5].同时也注意到环形振荡器电路中加入的电容量不能过大，尤其不能超过逆变器的输入电容以及串联的中间电容，避免整个系统的延迟效应被加入的电容所主导，从而影响研究结果.

3 电路模拟与仿真

为了更好地分析影响环形振荡器电路延迟效应的因素，对环形振荡器电路进行模拟与仿真.首先，在仿真软件中搭建出环形振荡器电路[6]，图3所示仿真电路为三态环形振荡器电路：

为了准确分析逆变器电容量和逆变器尺寸对电路延迟效应的影响，必须先计算出该仿真电路的延迟参数，才能确保系统仿真后得出的电路延迟时间的精确性.为此，应当计算出电路中的各个参数值，从而得出该电路的理论延迟时间.由电路基本公式可以得出：

图3 三态环形振荡器电路仿真图

d=Tpd÷tau（1）Tpd=d×tau（1）；d=g×h+p（2）；Tpd=tau*（g*h+p）=tau×（g×Cout÷Cin+p）（3）.由于p与等式中其他参数相比可以忽略不计，同时对于单逆变器，g=1，因此等式（3）可简化为Tpd= tau×Cout÷Cin.在仿真软件中，设置逆变器的尺寸为：常规的pmos管尺寸（长3.2 mm/宽0.6 mm），nmos管尺寸（长1.6 mm/宽0.6 mm），由该尺寸可以得出每个逆变器电容为6.592 fF（1fF=1×10^（-12）F），由于在相邻逆变器之间加入了10 fF的电容量，因而电路输出电容为6.592 fF+10 fF=16.592 fF[7].

根据以上电路参数进行系统的模拟与仿真，电路输入电压设置为4 V，控制逆变器的尺寸保持不变，代入以上系统参数值可以得到该电路延迟时间系数D为1ns，仿真结果如图4所示.

图4 三态环形振荡器电路仿真图（4V）

从图4可以看出系统延迟时间D=4ns÷4=1ns，与计算值相符.为了更进一步得到精确结果，改变4 V控制电压为2 V，输入电压的减少即相当于减少了电容的数量，同样方法得出D为1.312 ns，仿真结果如图5所示.

图5 三态环形振荡器电路仿真图（2V）

从图5可以看出系统延迟时间为D=1.312 ns，与计算值相符合.继续变换控制电压为8 V，输入电压的增加即相当于增加了电容的数量，计算得出系统延迟时间为D=0.992 ns，仿真结果如图6所示.

图6 三态环形振荡器电路仿真图（8V）

从图6可以看出系统延迟时间参数为D=0.889 ns，与计算所得值相差0.102 ns，误差在合理区间内，可以认定仿真得出的延迟时间为有效值.从图4至图6可以充分说明，系统延迟时间与电容量成反比，即电容量的增加会缩短系统的延迟时间，直接原因为电容量的增加会加快系统运行速度，从而缩短了系统的延迟时间.

另一方面，固定逆变器数量不变，输入电压仍控制在4 V，通过改变逆变器的尺寸同样也可以影响系统的延迟时间.将逆变器的尺寸调整为：pmos管尺寸（长32 mm/宽0.6 mm），nmos管尺寸（长16 mm/宽0.6 mm）.由于逆变器尺寸的扩大会同时造成本身电容量的扩大，为保持固定的电容量，根据电容串联容量减少的原理，将相邻串联逆变器的电容量增加至70 fF，以此抵消所减少的电容量，根据以上数值计算可得：D=454.7928 ps，即约等于0.45 ns，小于前文所计算得出的1 ns数值，进而可以得出结论：电路系统延迟时间与逆变器尺寸成反比，增大逆变器尺寸会缩短电路的延迟时间，直接原因是逆变器尺寸的增大会使更大电流流入逆变器，从而提高系统运行效率，进而缩短系统延迟时间.

4 结束语

通过研究环形振荡器电路中逆变器电容的数量和尺寸对电路性能的影响，分析得出了电路延迟时间分别与逆变器的电容量与尺寸均成反比的结论.采用的分析方法为定量分析法，即先固定逆变器的尺寸，通过变换输入电压来实现逆变器电容量的变换，从而分析逆变器的电容量给电路带来的影响.同样方法，固定逆变器的电容量，改变逆变器的尺寸，从而分析逆变器尺寸给电路带来的影响.因次，在实际搭建环形振荡器电路时，需要缩小逆变器的尺寸，同时尽可能扩大逆变器的电容量.上述结论对环形振荡器电路的实际应用具有指导意义，指明了提高环形振荡电路运行效率的方法.需要指出的是，此种类型的电路利用率还与供电电压和电路中电流电压分配等因素相关[8]，深入剖析影响环形振荡器电路性能的各类因素，进一步提高电路利用率，缩短电路延迟时间，是今后该领域工作的一个重要方向.

[1]Behzad Razavi.A study of noise in CMOS oscillators[J].IEEE J.Solid-State Circuit，1996，31（1）：331-343.

[2]Grey R，Meyer.Analysis and Design of Analog Integrated Circuit[M].2nd.New York:Wiley，1993.

[3]YAN W S T，LUONG H C.A 900MHz CMOS low-phase-noise voltage-controlled ring oscillator[J].IEEE Trans Circuits SystⅡ，2001，48（2）：216-221.

[4]刘祥昕，李文宏.与工艺、电源电压和温度无关的低功耗振荡环设计[J].固体电子学研究与进展，2010，30（2）.

[5]梁仲凯，罗胜钦.基于电感峰值技术的环形压控振荡器设计[J].电子测量技术，2010，33（5）：4-6+21.

[6]陈坤.电子设计技术[M].成都：电子科技大学出版社，2003.

[7]王松武，蒋志坚.通用仪器[M].哈尔滨：哈尔滨工程大学出版社，2002.

[8]谢自美.电子线路设计.实验测试（第二版）[M].武汉：华中科技大学出版社，2002.

Research and Analysis on Circuit Delay of Ring Oscillator

LI Chao-ran
（School of Computer Science and Information Engineering,Hanshan Normal University,Chaozhou,Guangdong,521041）

Ring oscillator is an important component of the circuit consisting computer hardware,which functions as signal output and amplification.The paper seeks out delay parameters of oscillator which have effect on the delay of whole circuit when running the simulation by using ring oscillator circuit.The number of inverters in the oscillator circuit and the size of the inverters are key points based on the structure of oscillator.By keeping the numbers of inverters fixed,one could observe the delay due to the change of size for each inverter. On the other hand,the effect on the delay for oscillator can be found to complete a whole logic process by varying the numbers of the inverters while making the size remained.During this two comparison process,the cause of the delay time change in an oscillator can be obtained.

ring oscillator；delay parameter；inverter

TP 331.2

A

1007-6883（2015）06-0035-05

责任编辑 朱本华

2015-09-29

李超然（1990-），男，广东潮州人，韩山师范学院计算机与信息工程学院教师.