一类具有脉冲免疫的时滞SIRS传染病模型的全局分析

吴燕兰， 黄文韬,2, 吴岱芩

(1.桂林电子科技大学 数学与计算科学学院 广西 桂林 541004; 2.贺州学院 数学系 广西 贺州 542800)



一类具有脉冲免疫的时滞SIRS传染病模型的全局分析

吴燕兰1， 黄文韬1,2, 吴岱芩1

(1.桂林电子科技大学 数学与计算科学学院 广西 桂林 541004; 2.贺州学院 数学系 广西 贺州 542800)

研究一类具有积分时滞的SIRS传染病动力学模型在脉冲免疫接种条件下的动力学行为. 运用离散动力系统的频闪映射, 获得一个“无病”周期解, 证明该“无病”周期解是渐近稳定的. 当模型的参数在适当条件下, 该“无病”周期解是全局吸引的. 运用脉冲时滞泛函微分方程理论获得带时滞系统持久性的充分条件, 也得到该模型的全局吸引性条件.

脉冲免疫； 周期解； 持久性； 积分时滞； 全局吸引性

0 引言

在传染病模型里,一般把总人口数N0分为易感者类S、染病者类I和恢复者类R.SIRS模型,它表示易感者被传染而成为染病者个体,染病者通过脉冲免疫接种具有免疫后从感染者类移出变为恢复者,恢复者渐渐失去免疫力后又变为易感者类.

近些年,有关传染病模型已有许多研究[1-9].文献[5]讨论了指数输入的SEIR预防接种模型,获得了无病平衡点和地方病平衡点全局渐近稳定性的充分性条件.文献[6]考虑了具有连续和脉冲预防接种的SIRS传染病模型,证明了无病平衡点和地方病平衡点全局渐近稳定性以及无病周期解的存在性与全局渐近稳定性.但同时考虑脉冲和时滞的模型较少.文献[7-8]考虑含有脉冲免疫时滞的SEIR模型.文献[9-10]研究了一个传染率形式λi(1+vik-1)s(λ>0,v≥0，k>0)的模型.文献[11]指出了在传染病模型中,积分时滞传染率λ∫f(s)s(t-s)i(t-s)e-usds比离散时滞的传染率更符合实际.文献[8]应用了同样的积分时滞传染率考虑SEIR模型,证明了积分时滞与脉冲免疫对模型的动力学行为产生显著的影响.本文在文献[6]中具有脉冲免疫及标准传染率的SIRS模型基础上,考虑了带有积分时滞传染率λ∫f(s)s(t-s)i(t-s)e-usds的SIRS模型.在传染病中，染病者及恢复者不是瞬间就得知感染或者已恢复,因此在染病者和恢复者中需要考虑模型含有时滞的情况.在文献[7,11-12]中,时滞流行病模型被广泛研究.本文提出了一个在脉冲免疫条件下含有脉冲预防接种治疗的带有积分时滞的SIRS模型,研究了其“无病”周期解、 持久性、 全局吸引性等动力学行为.

1 SIRS模型和预备知识

在SIRS模型的研究中,常常假定总人口N0的变动微小,在本文中我们假定总人口N0为常数.

考虑如下具有积分时滞和脉冲免疫的SIRS模型，

(1)

Ω={s≥0,i≥0,r≥0,s(t)+i(t)+r(t)=1}.

其中，s(t)=S(t)/N0,i(t)=I(t)/N0,r(t)=R(t)/N0分别为易感者比例、染病者比例和恢复者比例,b为出生率,λ为接触率,θ为染病者变为易感者的转移率,c为染病者变为恢复者的转移率,e为失去免疫率,u为自然死亡率,ε为因病死亡率,p为预防接种率.f(s)为[0,τ]上的非负函数,且满足

把r(t)=1-s(t)-i(t)代入式(1)中第1式,可知第1和2式不含r(t),所以只需要考虑以下子系统

(2)

下面给出一些将会在证明过程中用到的定义、符号和引理.

生物学上,我们只考虑系统(2)在如下的生物意义区域：

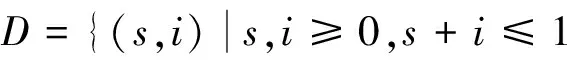
(3)

引理1[13]考虑下面的脉冲微分不等式

w(t)′≤(≥)p(t)w(t)+q(t),t≠tk,

这里p(t),q(t)∈C[R+,R],dk≥0以及bk是常数.假设

引理2[13]设V：R+×R+→R+,并且V∈V0.考虑

(4)

ψn:R+→R+是非减的.设r(t)是方程

其中x(t)是系统(1)在(t0,∞)上的任意解.

2 传染病灭绝周期解

i=0时,考虑以下子系统

(5)

对系统(5)在相临两次脉冲时间段内进行积分求解,得

(6)

上面的s(nT)表示在nT时刻的初始值.由系统(5)的第2个方程,通过频闪映射可得

(7)

因为f(s)所表示的直线斜率小于1,所以s*是全局渐近稳定的.进而可知系统(5)对应的周期解也是全局渐近稳定的.

把s*代入式(6)中的s(nT),得

(8)

是系统(5)的唯一全局渐近稳定的周期解.

易知系统(5)的解可以表示为

(9)

引理3s*(t)为系统(5)的唯一全局渐近稳定的正周期解,也就是,

为系统(1)的一个“无病”周期解(s*(t),0)关于

并且对系统(5)的每一个解s(t),当t→∞,s(t)→s*(t).

定理1 如果R1<1,且λs+e>θ,则系统(1)的“无病”周期解(s*(t),0)是全局吸引的.

证明 由于R1<1,则可以选取σ>0充分小,使得λ(δ+σ)<(u+c+ε+θ).

(10)

由上述分析可得

(11)

再由脉冲微分方程比较定理(引理2)知,存在一个整数k1>0,使得

nTk1,

(12)

进而由式(2)的第2个方程和式(12)可得

由式(1)的第1个方程可知

(13)

考虑比较系统

(14)

解得全局渐近稳定的正周期解

由引理2可知,存在k3>k2,使得

s(t)>x(t)-σ1,nTk3.

(15)

由式(12)和式(15),可得s*(t)-σ1

(16)

是全局吸引的.因此无病周期解(s*(t),0)是全局吸引的.证毕.

3 持久性

定理2 如果R2>1,则系统(1)的“无病”周期解(s*(t),0)是全局吸引的.

证明 假设X(t)=(s(t),i(t))是系统(2)满足条件(3)的任意一个解.由式(2)的第2个方程,得

(17)

(18)

因而存在充分小的正的常数ε1,使

(19)

(20)

类似,运用引理1,知道存在T1≥t0+τ,对t≥T1使

(21)

根据式(18)和式(21),可得

(22)

矛盾.因此对所有的t≥T1,有i(t)≥i(l)>0.于是由式(22),得

(23)

根据系统(2)的第1个方程和第3个方程,得

类似,根据引理1,可以选择t充分大,并且δ>0充分小,使得

取D={(s,i)∈R2|m1≤s(t),m2≤i(t),s(t)+i(t)≤1}.D是一个到坐标轴有正的距离的有界紧集.由上述讨论,可知系统(2)每一个满足初始条件(3)的解最终都进入并保留在D内.定理2证毕.

4 讨论

1)R1和R2正比于T且反比于p,意味着脉冲免疫接种阻止易感者被感染转到感染者这种行为.

2)R2与τ成正比,意味着疾病的染病未发作时期能够影响“染病者(I)”向“恢复者(R)”的转变.当疾病在传染期时间小于某个关键值时,疾病会自然消失.这可能是染病期间没有发作前死掉或者染病未发作期间由于接触感染源时间较短,免疫系统抵抗较强自动恢复,疾病消失.

3) 若λ的值越大,R1和R2的值都越大.说明它们对易感者向感染者的转化起到重大的作用.当λ很小时,系统的持久性消失,且传染病最终灭绝.

本文研究的是脉冲和积分时滞对SIRS模型的动力学影响.文中应用了脉冲泛函微分方程不等式的缩放处理进行分析,得到的不是精确的阈值,这需要以后进一步研究改进.

[1] 马知恩, 周义仓, 王稳地, 等. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004．

[2] 于育民, 宋苏罗. 一类SEIRS传染病模型的研究[J]. 郑州大学学报:理学版, 2011, 43(2): 4-9．

[3] D’Onofrio Alberto. Stability properties of pulse vaccination strategy in SEIR epidemic model[J]. Mathematical Biosciences, 2002, 179(1):57-72.

[4] 马知恩, 靳祯. 总人口在变化的流行病动力学模型[J].华北工学院学报, 2001, 22(4): 262- 271.

[5] Li Jianquan, Ma Zhien. Qualitative analyses of sisepidemic model with vaccination and varying total population size[J]. MathComputer Modelling, 2002, 35: 1235-1243．

[6] 靳桢, 马知恩．具有连续和脉冲预防接种的SIRS传染病模型[J]. 华北工学院学报, 2003, 24(4) : 235-243．

[7] Meng Xinzhu, Chen Lansun, Song Zhitao. The dynamics of a SEIR epidemic model concerning pulse vaccination strategy[J]. Applied Mathematics and Computation, 2007, 28(9) : 1123-1134.

[8] 刘开源, 陈兰荪. 一类具有垂直传染与脉冲免疫的SEIR传染病模型的全局分析[J]. 系统科学与数学, 2010, 30(3) : 323-333.

[9] Van den Driessche P, Watmough J. A simple SIS epidemic model with backward bifurcation[J]. Journal of Mathematical Biology, 2000, 40(6):525-540.

[10] Van den Driessche P, Watmough J. Epidemic solution and endemic catastrophes[J]. Fields Institute Communications, 2003, 36(1) : 247-257.

[11] Beretta E, Hara T, Ma Wanbiao, et al. Global asymptotic stability of an SIR epidemic model with distributed time delay[J]. Nonliner Analysis, 2001, 47(6) : 4107-4115.

[12] Ma Wangbiao, Song Mei, Takeuchi Y. Global stability of an SIR epidemic model with time delay[J]. Applied Mathematics Letters, 2004, 17(10) : 1141-1145.

[13] Lakshmikantham V, Bainov D D, Simeonov P S . Theory of Impulsive Differential Equations[M].New Jersey:World Scientific Pub Co Inc, 1989.

(责任编辑：王浩毅)

Global Analysis of a Delay SIRS Epidemic Disease Model with Pulse Vaccination

WU Yan-lan1, HUANG Wen-tao1,2, WU Dai-qin1

(1.SchoolofMathematicsandComputationalScience,GuilinUniversityofElectronicTechnology,Guilin541004,China; 2.DepartmentofMathematics,HezhouUniversity,Hezhou542800,China)

An SIRS epidemic disease model with pulse vaccination and integral delays was considered, and dynamics behaiors of the model under pulse vaccination were analyzed. By use of the discrete dynamical system determined by the stroboscopic map, an “infection-free” periodic solution was obtained and it iwas shown that the‘infection-free’ periodic solution was asymptotic stability. Then, it was proved that when some parameters of the model were in appropriate condictions, the ‘infection-free’ periodic sollution was globally attractive. Futher, with the theory on delay functional and impulsive differential equation, sufficient condiction with time delay for permanence of the system was given. At the same time, the condition of the global attractivity of the model was obtained.

pulse vaccination; periodic solution; permanence; integral delays; global attractivity

2015-05-13

国家自然科学基金资助项目，编号11261013；广西高校科研项目，编号KY2015ZD043.

吴燕兰(1990-),女,广东汕头人,硕士研究生, 主要从事微分方程及其应用研究,E-mail:wuyanlan90@163.com;通讯作者:黄文韬(1966-),男,广西永福人,教授,博士,主要从事微分方程定性理论研究,E-mail:huangwentao@163.com.

吴燕兰，黄文韬，吴岱芩.一类具有脉冲免疫的时滞SIRS传染病模型的全局分析[J].郑州大学学报：理学版，2015，47(3)：43-48.

O175.12

A

1671-6841(2015)03-0043-06

10.3969/j.issn.1671-6841.2015.03.008