带有自愿隔离博弈的SVIR传染病模型研究

张溶萍，刘茂省，解博丽

(中北大学，太原 030051)

0 引言

传染病对人们的生活具有极大威胁[1-3]。自从Kermack 等[4]提出传染病模型以来，大量的数学模型被用来分析各种传染病问题[5]，包括传染病的预防问题。疫苗接种和隔离是典型的预防策略。接种疫苗可以使个体产生抗体[6]，隔离可以阻断传染病的传播。

疫苗作为有效预防策略之一，被广泛运用于传染病预防和传播控制[7]。通过理论研究发现，自愿接种不太可能达到群体免疫水平，而且预期死亡率会大幅上升[8]，所以强制接种是必要的。实验表明，疫苗很少能对个体提供完全的保护，而且大部分疫苗的有效期有限[9]，所以本文模型中同时考虑了疫苗的有效性和有效期。Alexander等[10]研究了流感的传播动力学，并计算了控制流感所必须的阈值接种率。结果表明，如果疫苗有效率和接种率的综合作用达到阈值，流感的传播就可以得到控制。

隔离作为另一种有效的预防策略，在新冠病毒的预防中起了关键作用[11]。隔离感染者可以减少感染的发生。胡新利等[12]研究了SEQIJR传染病模型，发现适当地增加隔离强度有利于控制疾病的蔓延。丰利香等[13]建立了一类具有隔离和不完全治疗的传染病模型，并进行了理论分析，发现易感者自愿隔离可以防止自己被感染。Zhao等[14]建立了一种SEIR模型，将博弈理论决策过程的行为模仿纳入研究和预测COVID-19爆发的动力学过程。研究结果表明，个体层面采取预防感染的行为变化有可能在城市层面显著降低COVID-19暴发的规模和时间。Amaral等[15]提出了一种SIR 模型，使用演化博弈论刻画个体隔离策略的动态。结果表明，带隔离的情况出现了反复的感染波。

本文中提出一种结合疫苗接种和隔离的传染病模型，其中隔离的个体不具有传染性。根据实际情况，博弈论被用来描述易感者和接种者自愿隔离的选择。感染者以一定的速率隔离，直到恢复。模型中同时考虑了疫苗的有效性和有效期。

1 模型

同时考虑隔离和疫苗接种2种保护措施。隔离作为一种有效的预防措施，可以阻断传染病的传播，但会影响经济收入。接种疫苗可以使个体对传染病产生抵抗力，但疫苗的有效率不是100%。

所有个体被分成7类：未隔离的易感者Su，隔离的易感者Sq，未隔离的接种者Vu，隔离的接种者Vq，未隔离的感染者Iu，隔离的感染者Iq，恢复者R。Su(t)，Sq(t)，Vu(t)，Vq(t)，Iu(t)，Iq(t)和R(t)分别表示在t时刻，各类人口占总人口的比例，其中Su+Sq+Vu+Vq+Iu+Iq+R=1。未隔离的易感者的感染率用β表示。由于疫苗的有效性不是百分之百，所以接种疫苗的个体仍可能被感染。接种疫苗且未隔离的个体的感染率用δβ表示。感染个体的恢复率用γ表示。疫苗的接种速率为η。假设疫苗的有效期为1/ed，且恢复个体在1/ed后失去免疫。疾病的传播过程如图1所示。

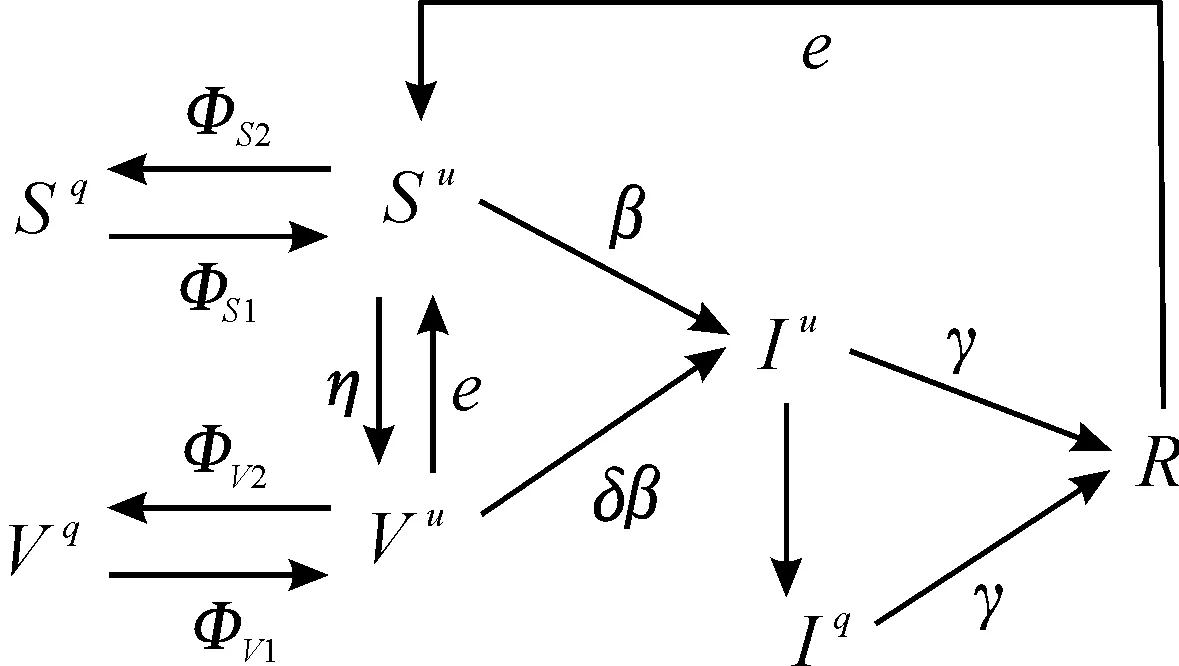
图1 疾病的传播过程示意图

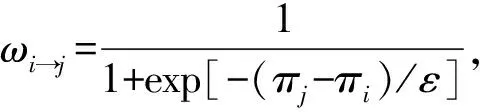
表1 收益矩阵元素

假设隔离个体的收益为-cq。接种且隔离的个体收益为-cq-cv。未隔离个体有感染的风险，假设未接种也未隔离的个体收益为-βIu，接种个体未隔离的收益为-δβIu。根据以上假设，建立动力学方程如下：

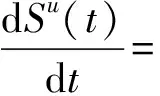
e(Vu(t)+R(t))-ΦS1(t)+ΦS2(t)

ΦV1(t)+ΦV2(t)

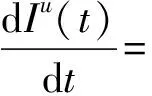
μIu(t)-γIu(t)

由于

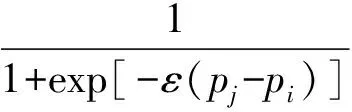
所以

代入上面的动力学方程，可得

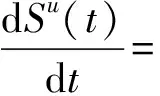
e(Vu(t)+R(t))-

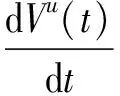
μIu(t)-γIu(t)

2 模型分析

模型的无病平衡点是

根据下一代矩阵法[16]，求得模型的基本再生数为

模型的地方病平衡点表示为E*=(Su*，Sq*，Vu*，Vq*，Iu*，Iq*，R*)。令等式右边为0，可得到以下等式：

定理1当R0<1时，无病平衡点E0是局部稳定的；当R0>1时，E0不稳定。

证明模型在无病平衡点处的雅可比矩阵为

3 数值模拟

通过理论分析得到无病平衡点、地方病平衡点和基本再生数，并分析无病平衡点的局部稳定性。模型中的预防措施包括隔离和疫苗接种，通过数值模拟分析它们对传染病的影响。

根据基本再生数的表达式可以看出：随着β和δ的增加，基本再生数增加；随着γ和μ的增加，基本再生数减少。接下来，通过作图分析e和η对基本再生数的影响。其他参数取值：β=0.375，δ=0.02，γ=0.125，μ=0.1。

从图2可以看出，随着η的增加，基本再生数减少；随着e的增加，基本再生数增加。在e和η较小时，基本再生数的变化速率较快；随着e和η的增加，基本再生数的变化速率减慢。基本再生数是判断传染病爆发的关键阈值，增加疫苗接种速率或感染者的隔离速率可以有效抑制传染病传播。

图2 参数对基本再生数的影响曲线

当基本再生数小于1时，无病平衡点稳定；当基本再生数大于1时，无病平衡点不稳定。取e=0.08，η=0.1，β=0.375和β=0.7进行验证，此时基本再生数分别为0.753 9和1.417 3，分析这2种情况下的时间序列。

图3中，竖线左侧表示当基本再生数小于1时各状态的时间序列，右侧表示当基本再生数大于1时各状态的时间序列。可以看出，当基本再生数小于1时，感染个体的比例很快趋于0，其他状态个体的比例稳定到无病平衡点。当基本再生数大于1时，感染个体的比例趋于一个稳定值。通过计算发现，感染个体比例的稳定值正好等于cq/β。在这2种情况下，接种疫苗的个体所占的比例均单调递减，这是由于隔离的收益小于不隔离的收益。对于疫苗接种个体而言，被感染的可能性很小，所以隔离不是最好的选择。

图3 无病平衡点的稳定性曲线

本文中的预防措施包括易感者接种疫苗，易感者的隔离，接种者的隔离和感染者的隔离。通过实验分析几种预防措施的有效性和它们之间的关系。模拟易感者隔离与不隔离时的差别。

图4中的曲线表示易感者不隔离时，各状态的时间序列。竖线左、右两边的图分别为原模型中，基本再生数小于1和大于1的情况。通过与图3对比可以发现，当β=0.375时，各状态的稳定值与易感者隔离时相同。当β=0.7时，易感者和接种者的稳定值变化不大，隔离与未隔离的感染者的比例明显增加。根据地方病平衡点的表达式可以得出，恢复者的比例也有增加。综上所述，当传染病形成地方病时，易感者的自愿隔离行为可以有效减少感染者的比例。

图4 易感者隔离对传染病的影响曲线

图5中的曲线表示不接种疫苗(η=0)的情况下，β=0.375和β=0.7时，各状态的时间序列。当β=0.375时，无病平衡状态变成了地方病平衡状态，所以疫苗接种很有必要。当β=0.7时，隔离与未隔离的感染者的比例变化不大，但隔离的易感者的比例明显增加。由于η=0，根据地方病平衡点的表达式可以得出，恢复者的比例减少。由此可以得出，当基本再生数小于1时，疫苗接种可以控制传染病的传播；当基本再生数大于1 时，疫苗接种可以减少易感者的自愿隔离比例。

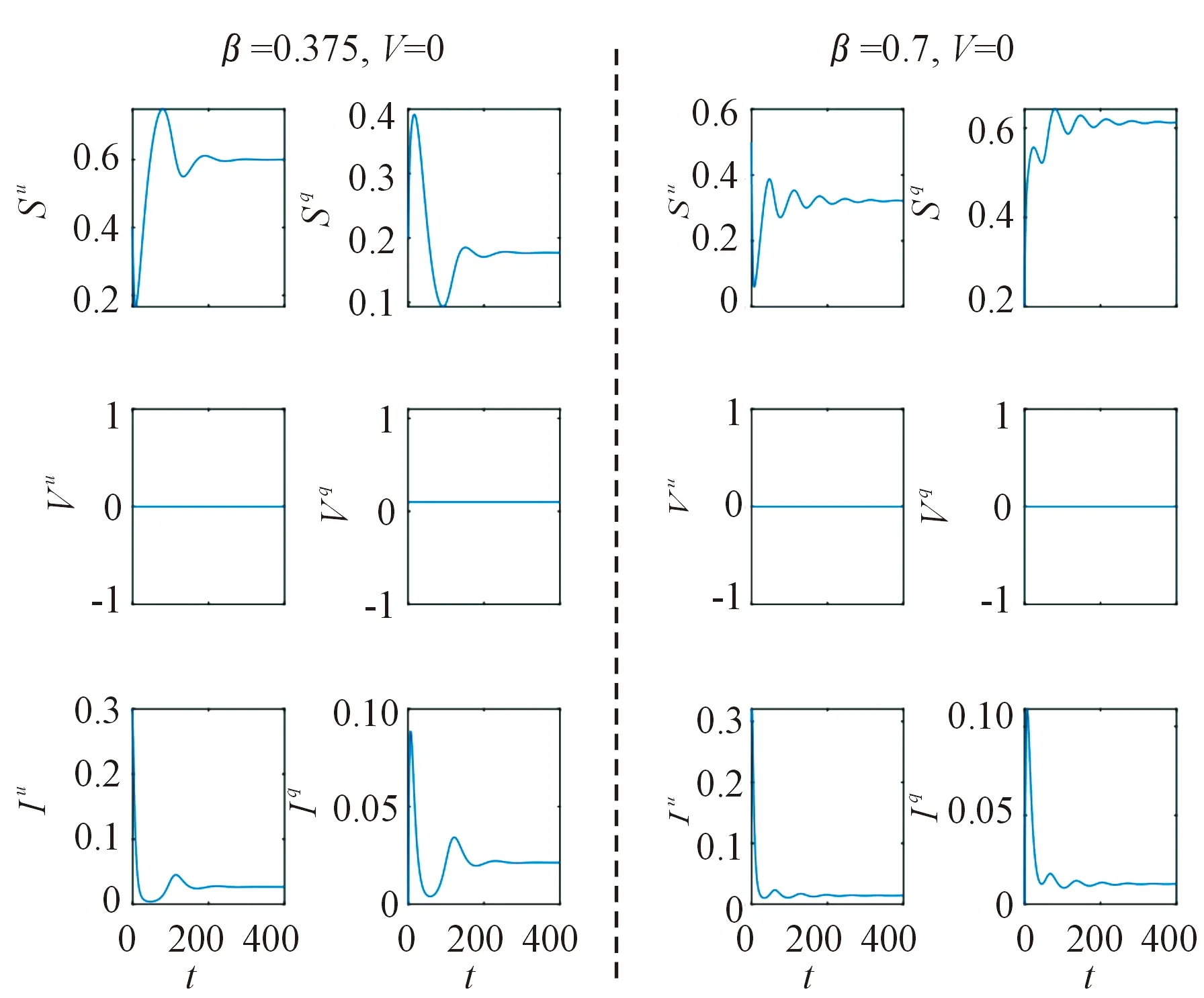
图5 疫苗接种对传染病的影响曲线

图6中的曲线表示不隔离感染者(μ=0)情况下，各状态的时间序列。明显地，当β=0.375时，无病平衡状态变成地方病平衡状态，所以隔离感染者很有必要。当β=0.7时，未隔离的易感者和未隔离的接种者减少，隔离的易感者增加。由此可以得出，当基本再生数大于1 时，隔离感染者会减少易感者的自愿隔离比例。

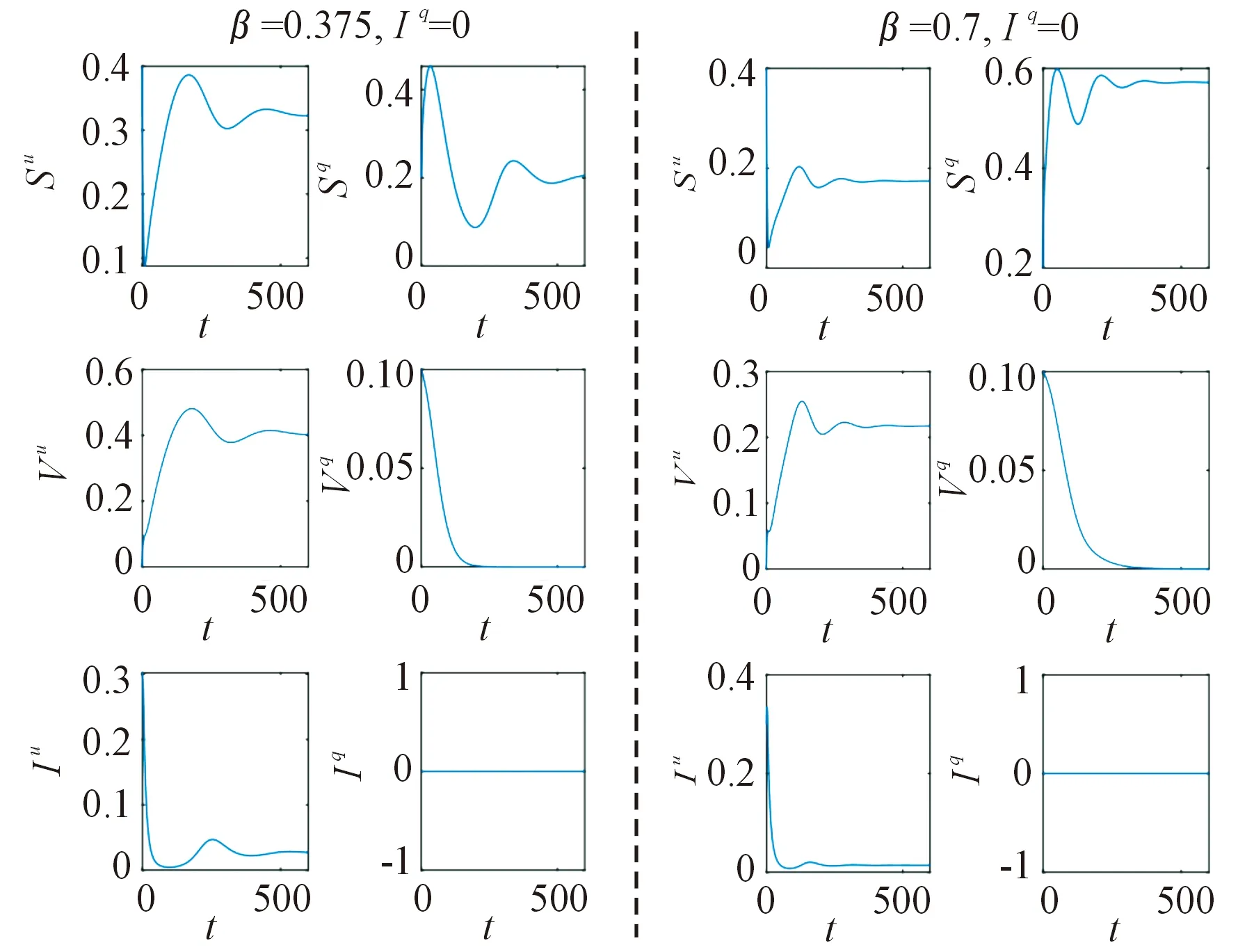
图6 隔离感染者对传染病的影响曲线

4 结论

考虑包含疫苗接种和隔离2种预防措施的传染病的传播模型，易感者和接种者的隔离用博弈论来刻画。通过理论分析，得到无病平衡点、地方病平衡点和基本再生数的表达式，并证明了无病平衡点的局部稳定性。

通过对比实验分析了隔离和疫苗接种对传染病的影响。结果表明，增加疫苗接种率可以减少基本再生数的值。当基本再生数大于1时，易感者的隔离可以有效减少感染者比例。