基于熵权法的实时振动信号存储管理技术

郭翠娟，龚楚云，荣 锋，宋雅琪

（天津工业大学电子与信息工程学院，天津300387）

基于熵权法的实时振动信号存储管理技术

郭翠娟，龚楚云，荣 锋，宋雅琪

（天津工业大学电子与信息工程学院，天津300387）

针对实时振动信号的存储问题，提出一种基于熵权法的实时振动信号存储管理模式.根据振动信号的波动特点，将采集到的信号波形从时域和频域2个方面分别计算出相关的指标参数，并采用熵权法对各参数进行加权计算，按照加权结果对各段波形进行排序，从理论角度对比甄选出含有有用信息较多的振动信号波形，舍弃较为无用的波形信号，从而节省数据库存储空间，方便后续信号的存储，而且使得有用波形可以完整携带并保存与机械运行状态相关的信号.

振动信号；大数据；熵权法；数据存储

对旋转机械的振动信号进行监测与处理有助于实时了解设备的运行状态[1].采集的振动信号通常被实时存储到数据库系统中，便于后续的分析处理.当前，国内外主流的工业实时数据库产品一般都提供了历史数据存储功能，能较长时间地保存备份现场所采集到的数据[2].由于机械需要长期运行，随着采集时间的增加，采集点增加，采集时间周期又较短，因此要保存的振动信号的数据量也随之不断增大，而数据库容量有限，如果将这些数据直接存储，不仅会占用大量的系统存储空间，无法满足长时间存储的需求，降低数据库的实时性，而且数据库的安全性和稳定性也会受到影响，数据的传输、查询将变得十分困难[3].

针对海量信息存储问题，传统的解决方案大多采用网络存储，然而网络存储需要专用服务器和专用磁盘阵列，成本昂贵，并且磁盘运行寿命有限，故障率高[4].而对数据库进行逻辑划分，即将数据分布到不同的服务器中进行存储，需要在数据增加时重新进行划分，进而要求修改程序并丢弃模型的独立性[5].对关系数据进行非规范化处理增加了数据的冗余，虽然有利于数据分布到多个节点上进行并行操作，却没能节省数据库容量.目前常用的数据压缩技术即对数据进行压缩再存储，可以提供较高的压缩率，因此历史数据占用的硬盘空间少，在存储及调用历史数据时对硬盘的读写减少，能够在保持数据库高实时性等特点的同时，尽可能地提高数据库的容量，从而节省了系统资源[6].数据压缩技术主要有有损压缩算法和无损压缩算法两种.有损算法依据数据的特征，通常采用了特殊舍点算法，该种算法会带来不可恢复的损失与误差，变换后数据变得很平滑，高值和低值被滤掉，也就不能准确地由波形信息推测出设备运行状态.而无损算法更不能从根本上解决数据库容量有限的问题.由此观之，在大数据背景下，信号处理的瓶颈已由“信号采集量太少”转移到“如何对海量信号数据进行高速有效处理”[7].

本文提出一种振动信号存储管理模式.根据振动信号的波动特点，计算所采集的信号在时域与频域中的相关指标参数，对这些参数按照熵权法[8]赋予权值进行加权计算，再将所采集的信号按照加权结果进行排序，对比甄选出含有有用信息较多的振动信号，节省数据库存储空间.

1 波形的指标参数计算

信号是信息的载体，选择适当的信号处理方法对信号进行处理，有利于后续的状态监测以及故障诊断工作的开展.通常，振动信号时域特征参数有振幅、周期、相位等，频域特征则主要包含在频率、能量信息中.采集板卡采集到振动信号之后，时域连续信号经过采样成为离散信号，上位机通过以太网接收离散振动信号，保存在数据库中.通过对离散信号进行分析处理，结合机械工作原理，可以对设备运行状态做出粗略的判断，为状态维修提供维修策略.

1.1 信号的时域指标参数计算

中心频率在信号的时域中描述幅值随时间的变化关系称作幅值域分析.幅值域分析是信号处理中最常用的信号分析方法.信号的幅值域参数主要包括峰峰值、峰值、均值、有效值、方差、峭度指标等：

（1）峰峰值，主要用来描述振动的幅值，即机械振动的位移量，由波形上最高点与最低点之差表示，计算公式为：

（2）峰值，是指波形上与零线最大的偏移量，振动信号的加速度值常用峰值描述.根据经验，一般在检测剥落、裂纹、压痕、凹坑等原因造成的冲击性振动时，峰值会急剧增大，计算公式为：

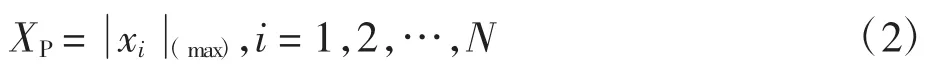
（3）均值，用来描述信号的平均水平，也称数学期望或一次矩，反映了信号变化的中心趋势，计算公式为：

（4）有效值，即信号的均方根值，可以描述振动的强烈程度，计算公式为：

（5）方差，反映了信号绕均值的波动程度，也是反映信号的离散程度，计算公式为：

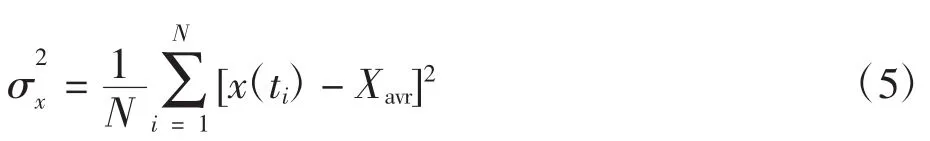
（6）峭度指标，可以敏感捕捉信号中的冲击成分，是描述波形尖峰度的指标，计算公式为：

峭度指标的计算公式中分子为x的4次方，而分母是一个平均量，这就必然导致分子的增加快于分母，若峭度指标的值上升很快，说明故障已出现，从而大大提高故障诊断准确度.

利用时域指标来分析振动信号，优点是直观、便于理解和直接计算，但只能做定性分析.从理论上讲，对信号来说，时域分析对时间的分辨率是无穷的，但对频率的分辨率为零；而频域分析对频率的分辨率是无穷的，但对时间的分辨率为零.因此，还需要结合信号的频域分析，才能更准确地评估出信号所包含有用信息量的多少，才能更有利于正确评估信号的有用价值.

1.2 信号的频域指标参数计算

频域和时域表明了动态信号的2个观察面，即这2种观察信号方法以不同的角度揭示了信号的物理特征，而傅里叶变换建立起它们之间的联系.

傅里叶变换可以看作是时间函数在频率域上的表示.由傅里叶变换给出的频率域包含的信息和原函数时间域内所包含的完全相同，不同的仅是信息的表示形式.根据振动信号采集已采样成为离散点存储在数据库的实际情况，本文选择更适合的离散傅里叶变换（DFT）来做离散信号的频域分析.DFT的表达方式如下：

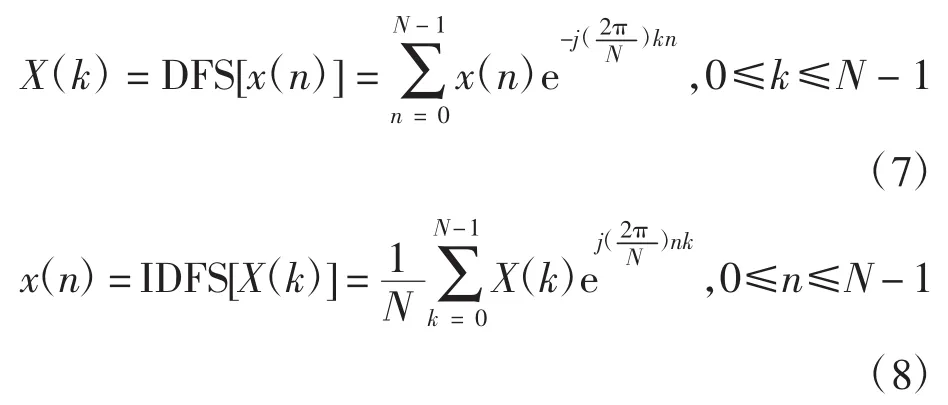
式中：DFS[*]表示离散傅里叶正变换；IDFS[*]表示离散傅里叶逆变换.利用傅里叶变换，可以得到幅度谱.在时间计算时，可以使用快速傅里叶变换（FFT），以减少运算量.

另外，功率谱也是一个常用的频域指标.功率谱反映了随机信号各频率成份功率能量的分布情况.当机械设备发生故障时，会在某些特征频率附近出现明显的峰值，功率谱反映了各频率成分能量的分布关系，更容易得到峰值所对应的频率，与设备特征频率进行对比分析，有助于对设备进行故障诊断.对于连续信号来说，当采样长度为T0时，其功率谱密度为：

当采样间隔为T、采样点为N时，T0=NT，由连续傅里叶变换和离散傅里叶变换关系得：

便可以得到离散功率谱密度表达式：

通过以上公式，可以将信号的使用价值大小定量化，方便作为后续排序的依据.

2 实时振动信号的存储管理

对振动信号分析中各指标参数的关心程度通常不尽相同，对于在监测机械运转与检测机械故障方面更能直观、方便和准确地提供信息的参数则应该多给予关心.本文方法的基本思想是：对于已经计算出来的各参数，对应地给予一组非负数权值ωi（i=1～n），然后将各指标参数计算值乘以相应的加权系数，求和，得到振动信号各项指标的加权结果.基于多指标与客观性考虑，本文选用熵权法进行权值的确定[9].

熵是信息论中的一个概念，熵权法的基本思路是根据指标变异性的大小来确定客观权重，在多指标综合评定方面几乎不受主观因素干扰，很有优势[10].一般来说，若某个指标的信息熵越小，表明指标值的变异程度越大，提供的信息量越多，在综合评价中所能起到的作用也越大，其权重也就越大.相反，某个指标的信息熵越大，表明指标值的变异程度越小，提供的信息量越少，在综合评价中所起到的作用越小，其权重也就越小[11-12].

利用熵权法，结合实际情况，本文所提出的振动信号指标参数加权计算过程如下：

（1）根据实际情况需要，将每一天的波形数据分为n组进行检测，即确定n个对象；

（2）计算出n组波形的时域以及频域各指标参数值，共有m项指标.从而得到矩阵：

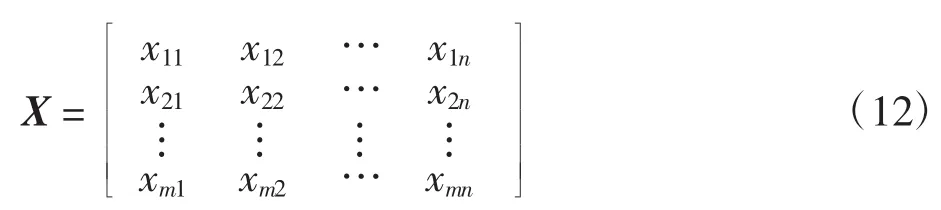
（3）对指标参数矩阵进行标准化处理得到新的矩阵：

式中：rij为第i个对象在第j个评价指标上的标准值.其标准化计算公式为：

公式（14）适用于指标数值越大越好的情况下，公式（15）则适用于指标数值越小越好的情况.

（4）计算第j项指标的熵：

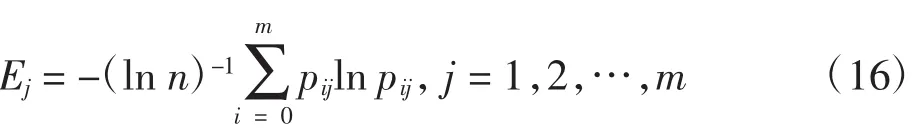
（5）计算各指标权重：

（6）根据各指标的熵与权值，便可以得到最终的加权结果Vi：

以上便是利用熵权法对振动信号的各项指标进行加权计算的全部过程.根据得到的加权结果Vi，便可以对抽取出来的波形信号信息量进行排序，从而删除包含信息量最少的信号，保留富含信息量的信号，方便后续的信号分析处理.

3 实验过程

振动信号存储在数据库中之后，根据实验需要，可以先抽取5组数据，按照上述方法进行计算.

本次实验利用振动信号采集系统分别采集5组波形，其中前4组分别为正常运行的波形产生的参数，第5组为故障波形产生的参数.正常振动时产生的波形以及故障时产生的波形分别如图1和图2所示.

图1 正常振动波形图Fig.1 Normal vibration signal

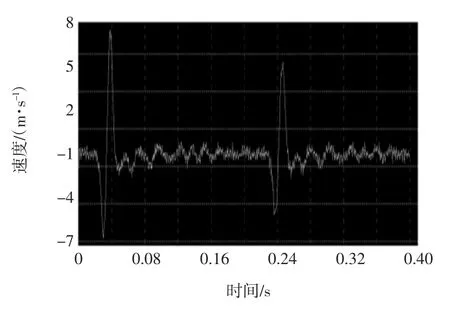
图2 振动故障波形图Fig2Vibration signal with bugs

根据前边所述过程，计算结果如表1所示.

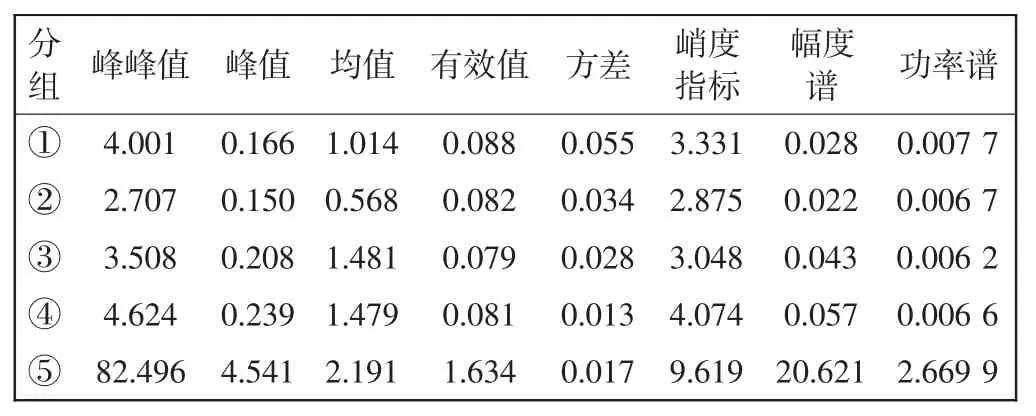
表1 5组振动波形各项指标计算结果Tab.1 Indexes of five vibration signals

对数据进行标准化后，得到结果如表2所示.

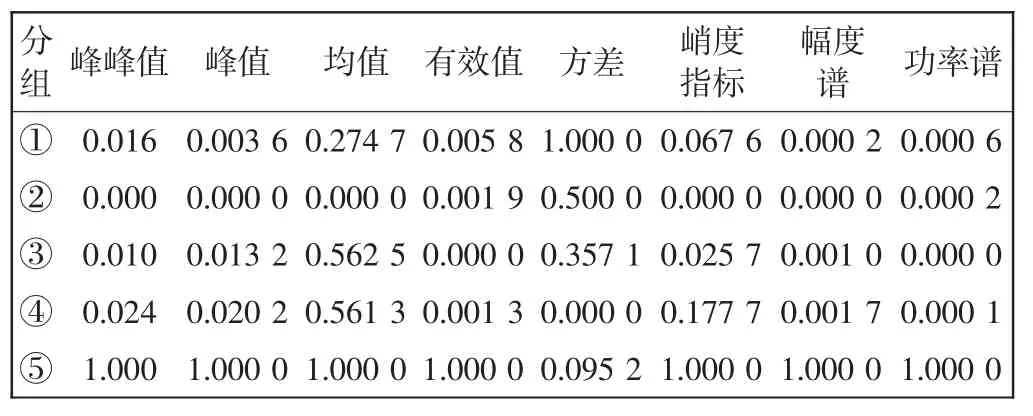
表2 5组振动波形各项指标计算标准化后结果Tab.2 Indexes of five vibration signals after standardization

根据信息熵的计算公式，得到各指标信息熵如表3所示.

表3 各项指标信息熵表Tab.3 Entropy weight of each index

根据得到的各指标信息熵，计算出各指标权重如表4所示.

表4 各指标权重Tab.4 Weight of each index

根据计算出的指标权重，5组波形加权结果如表5所示.

表5 5组波形评定结果Tab.5 Result of five wave caculate

根据最终的加权结果，可知第2组波形变化较为平缓，相应时段机械运转并无太大异常，所以并不需要对这一时段产生的波形做进一步地分析来得知机械是否故障，因此可以舍弃，节省数据库的存储空间.

4 结语

针对实时振动信号采集系统的数据库存储容量有限，数据不能长期稳定且安全地存储在数据库中，而压缩数据又不能完整还原波形信号的问题，提出一种新的振动信号存储管理模式，将采集到的振动信号波形从时域与频域2个方面分别计算出相关的波形指标参数，将计算得到的参数按照关心程度赋予权值，进行加权计算，便可以对各段波形按照权值进行排序，从理论角度对比甄选出含有有用信息较多的振动信号波形，继续保存在数据库中，舍弃较为无用的波形信号.这样不但节省了数据库存储空间，而且使得有用波形可以完整携带并保存与机械运行状态相关的信号.

本文提出的基于熵权法的实时振动信号存储管理模式，是基于实验室已有的硬件振动设备平台，研究平台上位机系统如何能应对硬件系统采集的大量振动信号数据而创新得出的一种大数据管理模式.由于该数据管理模式是基于信号特征参数计算得出的，而模拟和数字信号都有着诸如峰峰值、均值、有效值、方差和功率谱等相同的特征参量，因此理论上看似可以推广应用到其他信号如语音、视频、图像等信号的存储.但实际上，并不是所有信号都适用这一方法.因为在设备监测领域，一旦设备发生故障，设备故障部位产生的振动信号会发生突变，其各方面特征参量也有别于正常运作时产生的振动信号，因此通过算法计算，很容易找到突变信号而了解到故障所在.但语音、视频和图像信息的获取目的却与设备监测不同，或许并不是为了监测故障，而是为了进行图像或者语音信号的处理，那么按照本文方法并不能得出加权值大的信号就有利于信号处理的结论.非同一目的，不能混淆，这也是本文所提出的基于熵权法的实时振动信号存储管理模式的局限之处，还需作进一步研究.

[1]彭畅.旋转机械轴承振动信号分析方法研究[D].重庆：重庆大学，2014.

[2]赖达波.某齿轮箱故障振动信号特征提取及分析技术研究[D].成都：电子科技大学，2013.

[3]徐国风.实时数据库关键技术研究[D].西安：西安建筑科技大学，2006.

[4]吴剑强.流程工业实时数据库系统研究与开发[D].杭州：浙江大学，2004.

[5]栾振华.工业实时数据库的应用设计及数据处理研究[D].杭州：浙江大学，2008.

[6]HOURANI B，SALIM R.A performance analysis framework for the design of DSP systems.North Carolina State University，2008（4）：100-104.

[7]朱林.基于特征加权与特征选择的数据挖掘算法研究[D].上海：上海交通大学，2013.

[8]刘志，李军华，胡克泽，等.熵权法在企业绩效综合评价中的应用[J].石油化工管理干部学院学报，2008，4（10）：63-69.

[9]王昆，宋海洲.三种客观权重赋权法的比较分析[J].经济技术与管理研究，2003（6）：48-50.

[10]章穗，张梅，迟国泰.基于熵权法的科学技术评价模型及其实证研究[J].管理学报，2010，7（1）：34-41.

[11]高孝伟.熵权法在教学评优中的应用研究[J].中国地质教育，2008（4）：100-104.

[12]俞立平，武夷山.学术期刊客观赋权评价新方法：指标难度赋权法[J].现代图书情报技术，2011，27（4）：64-70.

[13]MENDAL Jery M.Tutorial on higher-order statistics spectra in signal processing and system theory：theoretial results and some applications[J].Proe IEEE，1991，49（3）：278-305.

[14]PORTNOFF M R.Time-frequency representation of digital signals and system based on short time Fourier analysis[J]. IEEE Trans on ASSP，1980，28：55-69.

[15]MALLAT S.Singularity deteetion and processing with wavelet [J].IEEE Trans Information Theory，1992，38（2）：617-693.

[16]MALLAT S G.A theory for multisolution signal decomposition：The wavelet representation[J].IEEE Transaetion on Pattern Analysis and Maehine Intelligence，1989，11（3）：674-693.

Storage management method of real-time vibration signal based on entropy weight technology

GUO Cui-juan，GONG Chu-yun，RONG Feng，SONG Ya-qi
（School of Electronics and Information Engineering，Tianjin Polytechnic University，Tianjin 300387，China）

Aiming at the stored problem of the real-time vibration signal，a storage management method of real-time vibration signal was presented based on entropy weight technology.The parameters of signal were calculated from timedomain and frequency-domain respectively，and each part of signal was evaluated with different weight valued parameters，then these signals were ordered，the useful signals with higher weighed result were kept and less useful signals with lower weighed results were deleted.This method can not only save the storage space of database for subsequent signals，but also store useful signals completely with useful information of machinery's states.

vibration signal；big data；entropy weight；data storage

TB535；TP311

A

1671－024X（2015）06－0067－05

10.3969/j.issn.1671-024x.2015.06.014

2015-07-07

国家自然科学基金资助项目（61405144）

郭翠娟（1975—），女，博士，副教授，主要研究方向为现代通信网络.E-mail：guocuijuan@tjpu.edu.cn