基于遗传规划的空空导弹攻击区拟合*

李枭扬,周德云,冯　琦,张华涛

(1　西北工业大学电子信息学院,西安　710072;2　中国兵器工业第203研究所,西安　710065)

基于遗传规划的空空导弹攻击区拟合*

李枭扬1,周德云1,冯琦1,张华涛2

(1西北工业大学电子信息学院,西安710072;2中国兵器工业第203研究所,西安710065)

摘要:针对传统空空导弹攻击区多项式拟合方法拟合模型固定,拟合精度较差等问题,提出一种基于遗传规划的空空导弹攻击区拟合方法。首先建立遗传规划空空导弹攻击区拟合模型,然后利用遗传规划算法对攻击区进行拟合,得到攻击区拟合多项式模型,最后通过非线性回归的方法对拟合得到的多项式模型进行回归分析,修正模型系数,得到最终的空空导弹攻击区拟合多项式。仿真实验证明了该算法比传统多项式拟合算法拥有更高的拟合精度。

关键词:空空导弹攻击区;遗传规划;曲线拟合;非线性回归

0引言

空空导弹攻击区是指目标周围的一个空间区域,载机在此区域内发射导弹,能满足脱靶距离的要求,并以一定的概率毁伤目标,是导弹系统作战效能的综合体现[1]。目前求解空空导弹攻击区的方法主要有快速模拟法[2-3]、插值法[4-5]、多项式拟合法[6]以及神经网络法[7-8]。快速模拟法为了提高计算速度,简化了导弹模型,精度较低。插值法为了满足精度的要求,需要大量的火控系统存储容量。神经网络法目前也只是处在研究阶段,还无法应用于火控系统攻击区的计算。由于多项式拟合方法将攻击区用多项式来表示,因此计算速度快,能够满足实时性的要求,并且对火控系统的存储容量要求较低,是一种较为理想的攻击区计算方法。但是空空导弹攻击区是攻击条件的非线性函数,由于目前多采用固定模型函数回归分析的方法实现模型的多项式拟合[5-6],无法全面描述攻击区的特征,拟合精度较差。

利用遗传规划算法对攻击区进行拟合不需要提前知道模型具体的函数形式,且所得到的模型能够较好的描述空空导弹攻击区的真实特征。鉴于目前求解空空导弹攻击区算法存在的问题,以及遗传规划的优点,文中提出一种基于遗传规划的空空导弹攻击区拟合方法,采用遗传规划算法确定攻击区的多项式模型,并利用非线性回归方法对多项式模型进行回归分析,以提高多项式拟合的精度。

1攻击区数学模型

影响空空导弹攻击区的主要因素有载机与目标高度,载机与目标速度,目标机动过载以及进入角。因此文中在仿真过程中采用的空空导弹攻击区数学模型描述如式(1):

(1)

式中:Rmax为攻击远界,Rmin为攻击近界;h为飞机高度,ht为目标高度;v为飞机速度,vt为目标速度;ny为目标机动过载;q为进入角。

2遗传规划算法攻击区拟合模型

2.1　遗传规划

遗传规划算法是在遗传算法的基础上发展起来的一种搜索寻优算法。虽然两种算法都是通过选择、交叉与变异等操作进行搜索寻优,但是遗传规划算法用分层结构来表示解空间,它的解的结构与大小是可以变化的,这就克服了遗传算法用固定字符串表示解的局限性,能够处理更加复杂的问题。

在空空导弹攻击区的拟合过程中,遗传规划算法不依赖于具体的函数模型,能够直接进行搜索。由于遗传规划解的形式是动态变化的,与传统的回归分析相比,其更适合于对空空导弹攻击区进行拟合。

2.2　终止集与函数集

选择空空导弹攻击区数学模型中的6个变量作为终止集T,如式(2)所示:

(2)

函数集F由基本算术运算符、三角函数以及对数函数组成,如式(3)所示:

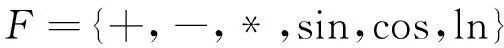
(3)

式中:“+,-,*”为基本算数运算中的加、减、乘;“sin,cos”为三角函数中的正弦、余弦;“ln”为受保护的自然对数,其具体形式如式(4):

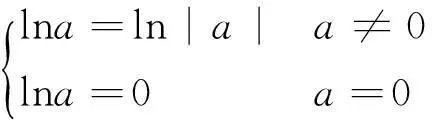
(4)

2.3　适应度函数

空空导弹攻击区拟合属于拟合预测类问题,对于此类问题通常利用残差和的大小来评价拟合的优劣,因此选取残差和作为适应度函数,适应度函数如式(5):

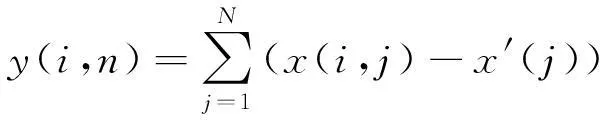
(5)

式中:y(i,n)为第n代群体中第i个体的适应度;N为输入的计算数据总个数;x(i,j)代表第i个个体在第j组计算数据中的返回值;x′(j)为第j组数据的真实值。显然该适应度越小代表拟合的精度越高。

2.4　遗传规划拟合攻击区算法步骤

步骤1对攻击区进行仿真得到n组攻击区数据。

步骤2确定算法的终止集与函数集。

步骤3随机产生N个初始多项式模型。

步骤4将n组攻击区数据分别代入N个多项式模型中,计算每个模型的残差和并将其作为个体的适应度。

步骤5进行选择、交叉以及变异等操作。

步骤6若满足拟合精度要求或达到最大迭代次数则停止算法,否则返回步骤4继续执行。

循环结束后,将最后产生的最优个体作为空空导弹攻击区的拟合多项式模型。

3多项式模型的非线性回归

3.1　高斯-牛顿法

由于遗传规划算法只能确定多项式模型,无法较好的确定多项式模型系数,且利用遗传规划算法得到的空空导弹攻击区拟合多项式模型是非线性的,因此需要利用非线性回归来修正多项式系数。文中采用非线性回归中最常用的高斯-牛顿法进行回归分析。

高斯-牛顿法的基本思想是使用泰勒级数的展开式来近似代替非线性模型,通过反复迭代,使得回归系数不断逼近最优的系数,最后使模型的残差平方和达到最小。

3.2　高斯-牛顿法迭代初值的选取

在高斯-牛顿法的应用过程中,迭代初值选择非常重要,若初值选择不当,则会导致迭代不收敛。

因为通过遗传规划得到的拟合多项式模型已带有系数,同时该多项式模型已经具备较好拟合精度,所以能够认为最优的拟合系数与原始模型系数相差不会过大,可以将多项式模型的原始系数作为初值,保证迭代在一定范围内能够收敛。

3.3　高斯-牛顿法拟合步骤

设含有n个自变量以及m个待定参数的非线性模型如式(6):

(6)

(7)

步骤2将非线性模型在α0处用一阶泰勒级数展开得式(8):

(8)

其中pi=(∂f(X,α)/∂αi)(i=1,2,…,m)。

步骤3合并所有N个观测值得到式(9):

(9)

其中:Y(α)为N维向量,其第i维向量为yi=f(X,α),P0为N×m阶导数矩阵,Δα为N维参数向量。

式(8)移项得到残差Z(α)的近似表示:

(10)

步骤5若迭代达到收敛则停止算法,若未收敛则返回步骤1继续执行。

4仿真实验

为了便于分析,在仿真中作如下假设:

1)目标与载机大致在同一高度。

2)目标做匀速直线运动。

3)载机是指向目标飞行的。

取90组攻击区数据并利用遗传规划进行拟合,仿真环境为Matlab 2012。选取初始种群为200,迭代次数为300,选择概率与交叉概率采用文献[9]中提出的算法,该方法能够有效避免种群的早熟收敛。由于攻击区远界和近界的拟合分析方法相同,因此文中只对攻击区远界进行拟合分析。通过遗传规划得到的空空导弹攻击区拟合多项式模型如式(11):

(11)

式中{a1,…,a46}为待拟合系数。

取载机与目标高度为8 000 m,目标速度为220 m/s,载机速度为320 m/s,目标机动过载为1,同时选取文献[6]中空空导弹攻击区拟合多项式模型进行拟合分析,得到采用固定多项式模型拟合攻击区与理论攻击区对比如图1。

在同样的条件下采用遗传规划拟合多项式模型得到的攻击区与理论攻击区对比如图2。

在同样条件下采用非线性回归的遗传规划拟合攻击区与理论攻击区对比如图3。

由图1可见,朝向目标移动方向的部分攻击区(极坐标中[330,30]范围内的攻击区)曲线变化程度与其他部分相比较剧烈,非线性程度较强,因此采用传统固定多项式模型的拟合方法在该范围内误差较大。而图2中采用遗传规划拟合多项式的拟合方法在该范围内误差较小,因此说明采用遗传规划拟合多项式的拟合方法比采用传统固定多项式模型的拟合方法能更好的描述攻击区的特征。

由图3可见,采用非线性回归分析后的遗传规划拟合方法与没有进行回归分析的图2中方法相比,其拟合精度明显提高。

图1　采用固定多项式模型的拟合攻击区与理论攻击区对比

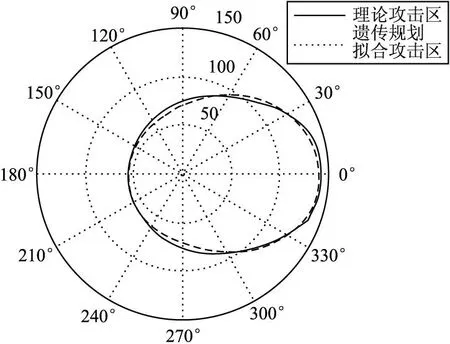
图2　遗传规划拟合攻击区与理论攻击区对比

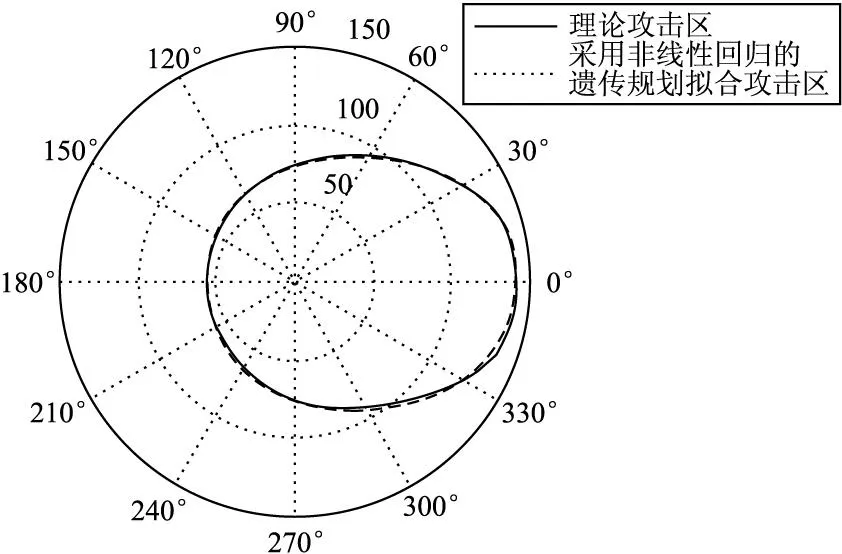
图3　采用非线性回归的遗传规划拟合攻击区与理论攻击区对比

采用失去发射机会的概率Pml、界外发射概率Pob和平均发射成功概率P来表示拟合的精度。采用固定多项式模型的拟合算法(算法1)、采用遗传规划多项式模型的拟合算法(算法2)和采用非线性回归的遗传规划多项式拟合算法(算法3)3种拟合方法的精度对比如表1。

表1　3种拟合方式的精度对比

由表1可见,文中提出的基于遗传规划的空空导弹攻击区拟合方法比传统采用多项式拟合方法的拟合精度更高。

5结论

文中提出一种基于遗传规划的空空导弹攻击区拟合方法,该方法克服了传统多项式拟合方法拟合模型固定的问题,提高了拟合精度。值得说明的是,遗传规划算法是一种搜索寻优算法,而每次通过遗传规划得到的拟合多项式模型都是不同的,这些模型的拟合精度有高有低,因此在实际应用中若增加拟合的原始数据,并利用大型计算机对数据进行多次拟合,能够得到更为理想的结果。

参考文献:

[1]郑志伟. 空空导弹系统概论 [M]. 北京: 兵器工业出版社, 1997.

[2]张平, 方洋旺, 金冲, 等. 空空导弹攻击区实时结算新方法 [J]. 弹道学报, 2010, 22(4): 11-14.

[3]杜昌平, 周德云, 江爱伟. 一种空空导弹可攻击区快速算法 [J]. 西北工业大学学报, 2006, 24(6): 682-685.

[4]王宏伦, 佟明安. 空空导弹攻击区处理的拟合——插值法 [J]. 火力与指挥控制, 1998, 23(4): 14-18.

[5]王宏伦, 张安, 张海, 等. 空-空导弹攻击区的高精度快速拟合 [J]. 航空学报, 1997, 18(5): 631-632.

[6]杜昌平, 周德云, 阳治平. 基于遗传算法的空空导弹弹道拟合方法 [J]. 西北工业大学学报, 2003, 21(2): 172-175.

[7]逮宏亮, 张艺瀚, 李伟仁. 基于RBF网络的导弹攻击区解算及对比分析 [J]. 火力与指挥控制, 2004, 29(5): 47-50.

[8]张列航, 雷蕾, 李研生. BP神经网络导弹攻击区火控工作式拟合 [J]. 火力与指挥控制, 2011, 36(12): 177-179.

[9]Davis L. Adapting operator probabilities in genetic algorithms [C]∥Proceedings of the 3rd International Conference on Genetic Algorithms, 1989: 61-69.

收稿日期:2014-05-08

基金项目:航空科学基金(No.20115553021)资助

作者简介:李枭扬(1989-),男,陕西西安人,博士研究生,研究方向:弹道设计,导弹制导。

中图分类号:TP181

文献标志码:A

Air-to-air Missile Launch Envelops Fitting Based on Genetic Programming

LI Xiaoyang1,ZHOU Deyun1,FENG Qi1,ZHANG Huatao2

(1School of Electronics and Information, Northwestern Polytechnical University, Xi’an 710072, China;

2No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)

Abstract:For the problem that fitting model is fixed and precision is low of traditional air-to-air missile launch envelops fitting method, an air-to-air missile launch envelops fitting method based on genetic programming was proposed. Firstly, an air-to-air missile launch envelops fitting model based on genetic programming was established. Secondly, the air-to-air missile launch envelops was fitted by genetic programming algorithm so as to get polynomial fitting model. Finally, regression analysis on the polynomial model was performed by nonlinear regression method in order to update the model coefficient and get the final air-to-air missile launch envelops fitting polynomial. The simulation results show that this algorithm is higher in precision than traditional polynomial fitting algorithm.

Keywords:air-to-air missile launch envelops; genetic programming; curve fitting; nonlinear regression