基于RBFNN增益调节的自适应滑模制导律*
李 解,雷虎民,王华吉,朱苏北
(空军工程大学防空反导学院,西安 710051)
基于RBFNN增益调节的自适应滑模制导律*
李解,雷虎民,王华吉,朱苏北
(空军工程大学防空反导学院,西安710051)
摘要:为提高末制导精度,设计了一种RBF滑模制导律。根据滑模变结构理论推导了一种基于零化视线角速率的滑模制导律,分析了目标机动与切换项增益的关系,利用RBF神经网络对切换项增益进行在线估计,最后将所设计的RBF滑模制导律与滑模制导律、比例导引律进行仿真对比。仿真结果表明所设计的制导律能实时调节切换项增益,有效拦截不同的机动目标,减小了脱靶量并提高了系统的鲁棒性。
关键词:滑模制导律;RBF神经网络;切换增益
0引言
近年来,由于对外界干扰和参数摄动具有良好的鲁棒性,滑模变结构控制理论被应用于导弹制导律的设计之中。
文献[2]提出了适用于拦截高速大机动目标的自适应变结构导引律(ASMG),证明了该导引律对外界干扰和参数摄动具有不变性。其设计的制导律含有切换项增益,该增益要随外界干扰等因素的变化而变化,所以不易确定,过大容易使接近滑模面时出现抖振,过小则会造成导弹脱靶。文献[3]将制导过程中的目标机动视为一个有界复合干扰,运用RBF神经网络能以任意精度逼近非线性连续函数的特性,对干扰进行逼近,从而提高制导律的鲁棒性。
文中结合滑模变结构理论和RBF神经网络算法,以视线角速率为滑模面设计滑模变结构制导律。通过RBF神经网络,以视线角和滑模面作为输入,对切换增益进行自适应调节,从而达到提高鲁棒性的目的。
1三维弹目相对运动模型建立
建立三维弹目相对运动模型如图1所示。

图1 弹目相对运动关系
图中:xiyizi为惯性坐标系,xLyLzL为视线坐标系,xvyvzv为弹道坐标系,M为导弹,T为目标,θM、ψM、θT、ψT、θL、ψL分别为导弹,目标和视线的倾角和偏角。
设导弹和目标的速度分别为VM和VT,aMy和aMz分别为导弹俯仰通道和偏航通道的加速度,aTy和aTz分别为目标俯仰通道和偏航通道的加速度,弹目相对距离为r。
由图可得:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
对式(2)、式(3)求导结合式(4)~式(7)得到:
2基于零化视线率的滑模制导律设计

现将三维弹目相对运动关系分为俯仰通道和偏航通道分别进行分析。
2.1 俯仰通道
为使导弹能准确命中目标,根据平行接近原理,在拦截过程中希望视线角速率趋近于零。因此选滑模面为:
(10)
为保证系统状态能到达滑模面且到达的过程中有优良的动态特性,文中采用趋近律方式推导导引律。
(11)

结合式(8)、式(10)、式(11)可得:
(12)
2.2 偏航通道
与俯仰平面同理,以偏航角速率为滑模面:
(13)
结合式(9)、式(11)、式(13)可得:
(14)
3基于RBF神经网络的自适应增益调节
由式(12)、式(14),所求得的滑模制导律中含有切换控制量εsgn(s)。在导弹拦截目标时,目标机动与滑模制导律的切换控制量均与视线角速率成正比[7]。只要ε取值合适,就能抵消目标机动造成的视线角速率变化。若ε取值不合理,则会造成脱靶。
根据仿真得到的结果,ε变大时,视线角速度收敛快,末端最大需用过载小,但是随着ε越大,抖振也越明显。而ε过小时,视线角速率、导弹过载受目标机动影响变得明显。
因此,文中利用RBF神经网络,对切换增益进行自适应调节,从而达到提高鲁棒性和减小脱靶量的目的。

(15)
其中:cj为隐层第j个神经元的中心位置向量,bj为基宽度参数,‖·‖表示欧氏范数。指定输入层神经元到隐层神经元之间的权值为1,隐层神经元到输出层神经元的权值向量为w。
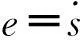
(16)
由梯度下降法可得网络权值的学习算法为:
(17)

综上,网络权值的学习算法为:
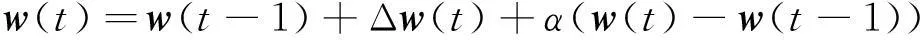
(18)
其中α为惯性量系数,α∈(0,1)。
4仿真分析
为了验证文中的自适应增益调节滑模制导律,利用Matlab进行了三维模型仿真。仿真参数见表1。
仿真结果取俯仰平面的结果数据进行说明。文中所设计的制导律与滑模制导律分别简称为RBFSMG和SMG。

表1 弹目运动及RBF神经网络初始参数
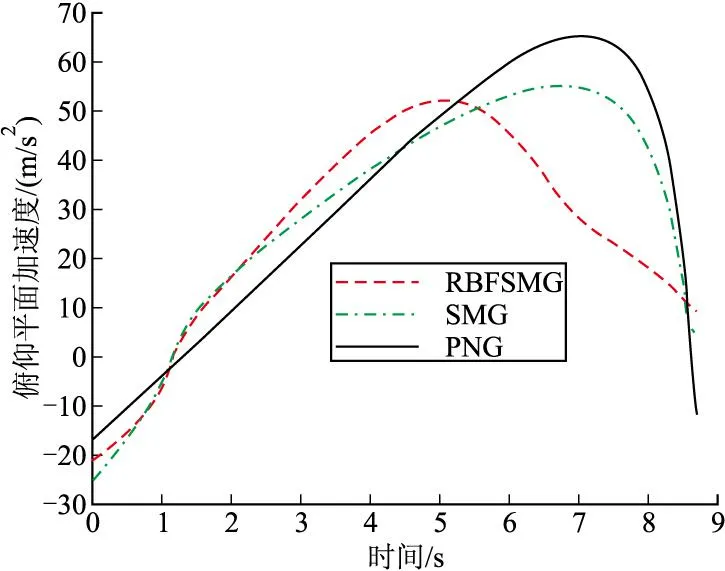
图2 3g机动俯仰平面加速度
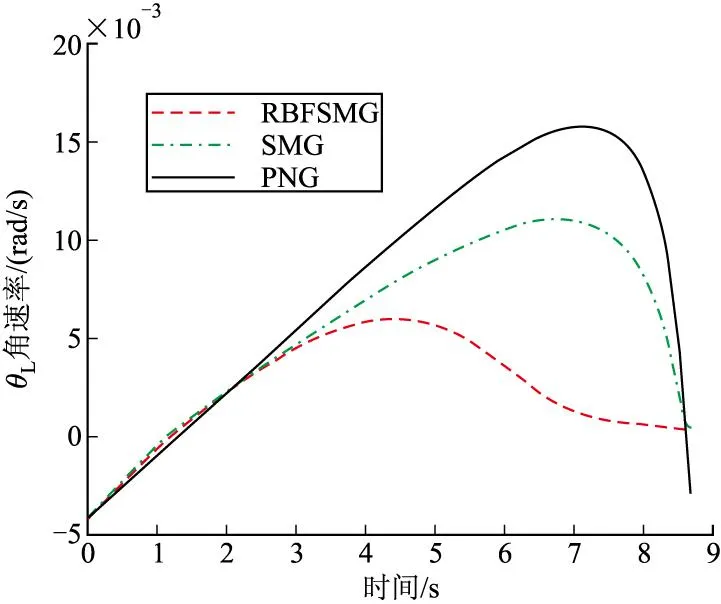
图3 3g机动时视线倾角速率
由图2和图3可知,在目标机动大小为3g情况下,RBFSMG视线角速率收敛迅速,视线角变化幅度小,整个导引过程中导弹飞行较为平滑,较之SMG,也有明显的优势。同时,与PNG相比,PNG所需的最大过载加速度为6.5g,RBFSMG只需5g,且到达最大值后迅速减小,逐渐趋向于0。
由图4~图6可知,在目标有最大10g的正弦机动情况下,SMG由于切换增益固定,导引过程的末端视线角速率突增,需用过载变大,脱靶量4.118 m;而RBFSMG由于对切换增益进行了自适应调节,对目标机动带来的影响一直有着良好的抵消作用,全程加速度变化较为平滑,末端优于SMG和比例导引律,且视线角速率收敛至0,脱靶量为0.294 m;比例导引律在末端受目标机动影响明显,脱靶量为11.189 m。
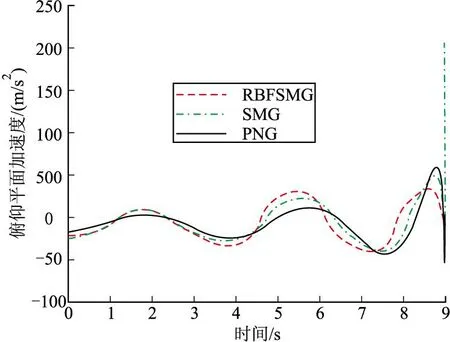
图4 正弦机动俯仰平面加速度

图5 正弦机动时视线倾角速率

图6 滑模切换增益
因此,可以说明,基于RBF神经网络增益调节的滑模制导律,在目标机动越明显的情况下越优于固定系数的滑模制导律,可有效减小脱靶量并增强系统鲁棒性。
5结论
文中结合滑模控制理论和RBF神经网络,设计了基于RBF神经网络增益调节的自适应滑模制导律,利用RBF神经网络对切换增益进行了在线调节。
仿真结果表明在存在目标机动的情况下,该制导律有效减小了脱靶量,并增强了系统的鲁棒性, 具有一定的参考价值。
参考文献:
[1]H M Prasanna, D Ghose. Retro-proportional-navigation: A new guidance law for interception of high-speed targets [J]. Journal of Guidance, Control, and Dynamics, 2012, 35(2): 377-386.
[2]Di Zhou, Chundi Mu. Adaptive sliding-mode guidance of a homing missile [J]. Journal of Guidance, Control, and Dynamics, 1999, 22(4): 589-594.
[3]刘国琴. 基于神经网络的导弹变结构制导律 [J]. 电光与控制, 2009, 16(4): 44-45.
[4]李士勇. 智能制导: 寻的导弹智能自适应导引律 [M]. 哈尔滨: 哈尔滨工业大学出版社, 2011: 129-143.
[5]Yuri B Shtessel, Ilya A Shkolnikovb. Smooth second-order sliding modes: Missile guidance application [J]. Automatica, 2007, 43(8): 1470-1476.
[6]刘金琨. 滑模变结构控制MATLAB仿真 [M]. 北京: 清华大学出版社, 2005: 228-235.
[7]闫斌斌. 针对目标机动的变结构制导参数设计 [J]. 西北工业大学学报, 2009, 27(4): 500-501.
收稿日期:2014-05-13
基金项目:航空科学基金(20130196004)资助
作者简介:李解(1991-),男,江苏镇江人,硕士研究生,研究方向:飞行器制导与控制。
中图分类号:TJ765.3
文献标志码:A
Adaptive Sliding Mode Guidance Law Based on RBFNN Gain Regulation
LI Jie,LEI Humin,WANG Huaji,ZHU Subei
(Air and Missile Defense College, Air Force Engineering University, Xi’an 710051, China)
Abstract:To improve accuracy of guidance system in terminal guidance phase, a RBF sliding mode guidance law was designed. A sliding mode guidance law based on zeroing line of sight rate was deduced with the theory of sliding mode variable structure control. With analysis of relationship between target maneuvering and switch gain, RBF neural networks were used for switch gain online regulation. Finally, compared with sliding mode guidance law and proportional navigation, the simulation results show that the RBF sliding mode guidance law has stronger robustness for target maneuvering and reduces target-missing effectively.
Keywords:sliding mode guidance; RBF neural networks; switch gain

