基于张力格林样条的EMD均值曲线插值方法

戴豪民，许爱强

（海军航空工程学院 飞行器检测与应用研究所，山东 烟台264001）

0 引 言

经验模式分解 （empirical mode decomposition，EMD）是一种自适应信号分解方法，适用于分析非线性、非平稳信号［1］。经 典EMD 方 法 采 用 三 次 样 条 插 值 （cubic spline interpolation，CSI）拟合信号的上、下包络线，从而获得信号的均值曲线。实验结果表明，CSI方法拟合的包络线经常会出现过冲现象，造成均值曲线的误差较大。目前，针对CSI方法中出现的曲线过冲现象，已经提出了多种改进方法。文献 ［2］指出三次样条曲线是二阶光滑的 （二阶连续可导），过冲的主要原因是曲线的 “柔性”不够，会在临近间隔大且缺少约束的插值点之间出现剧烈振荡 （如图1所示），遂提出分段幂函数插值法，通过牺牲曲线的光滑性使包络线更具 “柔性”。其幂指数可以取任意大于1的整数或小数，但随着幂指数的增大，计算时间也显著增加。通过实验验证，当幂指数β＝2.5时，包络线同时具备较好的光滑性和柔性，但此时包络线仍然只有一阶光滑性 （一阶连续可导）。文献 ［3］指出过冲的原因是由于CSI方法在待拟合的两个邻近插值点之间不具备单调性，提出分段三次 厄 米 特 插 值 法 （piecewise cubic hermite interpolation，PCHI），它能够使待拟合的两个邻近插值点之间具备单调性，较好克服包络插值过程中出现的过冲现象，但包络线只有一阶光滑性，只能保证各段曲线在连接点处的连续性，不能保证插值曲线在这些点上的光滑性。另外，文献 ［4］提出B样条插值法，该方法是为了便于对EMD 分解进行理论分析而引入的一种替代方法，插值特性并没有显著提高［5］。

图1 三次样条、无张力格林样条和张力格林样条对离散数据点插值结果

本文针对EMD 的包络插值问题，提出采用张力格林样条 插 值 方 法 （Green’s spline interpolation in tension，GSIT），在不牺牲包络线光滑性的前提下，减轻包络线的过冲问题，另外，采用极值中点的一次插值也能进一步降低信号分解的误差。通过对仿真和实际信号的分析验证了该方法的有效性，其能够使EMD 分解更加精确。

1 格林样条插值原理

1.1 无张力格林样条插值

格林样条插值又叫双调和样条插值，它是一种基于双调和算子的全局插值法［6］。在一组不规则的数据点之间，通常可以利用三次样条插值找出通过这些数据点的光滑曲线。从弹性力学的角度上看，就是求解弹性细杆在不同位置上受到点压力作用下的弯曲变形问题［7］，这样受位于xj点的垂直集中力δ（x－xj）作用的弹性细杆，其位移函数g（x）满足以下双调和方程

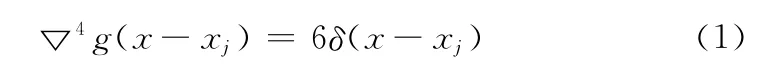
式中：4——双调和算子，xj——弹性细杆的受力位置，δ（x）——Delta函数。式 （1）的特解是

当对位于xj（j＝1，2，…，N）的N 个数据点wj进行插值时，需要求解的双调和方程就成为

式中：αj是加权系数，w（xj）是内插曲线在位置xj处的位移。式 （3）和式 （4）的特解w（x）可以表示成各个点压力的格林函数的线性组合，即

加权系数αj可以通过解下面线性方程组获得

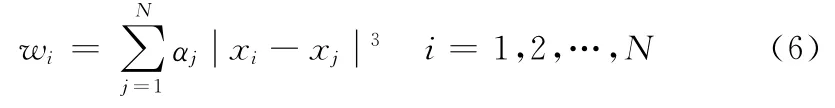
确定αj后，就可以利用式 （5）计算任一点x处的插值函数值w（x）。

1.2 张力格林样条插值

无张力格林样条只受到垂直方向力的作用，水平方向并未受到力的作用。由图1可见，无张力格林样条插值会在一些数据点间出现大幅度的振荡，尤其是数据点间隔较大时，由于水平方向未受力的作用，这种变化更为明显。通常情况下，这种大幅振荡现象在三次样条插值过程中也会出现。为避免出现这种欠合理的现象，可以通过在格林样条中引入张力参数，从而获得更为真实的曲线形状［8］。

当弹性细杆同时受到水平张力p ＞0作用时，其位移函数gp（x）满足以下双调和方程

式中：2——调和算子，该方程的一个特解是

通过N 个数据点的受张力p 的位移函数wp（x）为

与式 （6）类似，式 （9）中的加权系数αj可以通过以下线性方程组得到

1.3 计算实例

2 实验分析

为了验证格林样条插值在经验模式分解中的效果，本文选取EMD 中最为常用的两种插值方法——三次样条插值和分段三次厄米特插值与其进行对比，采用正交指数 （index of orthogonality，IO）和能量相对误差 （energy relative error，ERE）评价各种插值方法的性能

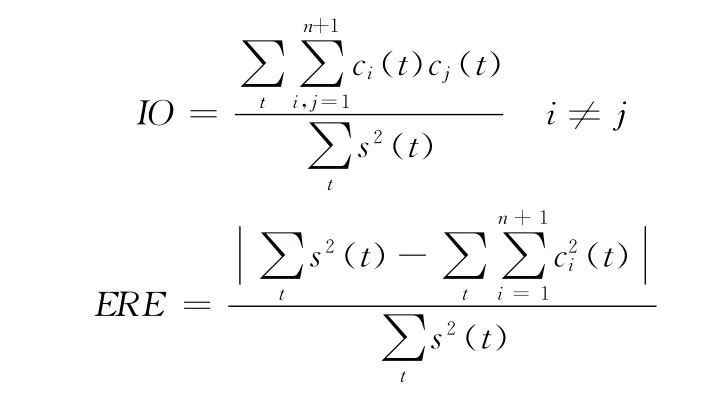
其中，s（t）表示信号，ci（t）表示EMD 分解得到的第i个imf分量。IO 指标越接近于0，说明EMD 分解得到的各个imf分量之间越接近于正交。ERE 指标越接近于0，说明EMD分解能量损失越低。

2.1 仿真信号分析

考察以下多分量信号：s（t）＝sin（20πt）＋sin（50πt）＋sin（140πt）t∈［0，1）求取其极大值后，采用3种方法拟合的该信号上包络线，如图2所示 （截取信号中0.16～0.23段表示，张力参数取0.5），从图2中A 点可以看出，CSI方法和GSIT 方法拟合得到的包络线在此处存在过冲现象，过冲程度GSIT 方法要轻于CSI方法，而PCHI方法则不存在过冲问题；在B 点，由于PCHI方法要保证插值曲线的单调性，3种方法均出现过冲现象，其过冲程度PCHI方法最轻，GSIT 方法次之，CSI方法最差。从信号拟合的包络线来看，PCHI方法只存在一阶导数，其光滑性最差，后续的分解情况会发现，虽然PCHI方法过冲现象最不明显，但其分解误差却是最大的，这主要是由于包络线的光滑性差造成的；GSIT 方法存在四阶导数，在保证包络线光滑性的情况下，一定程度上克服了三次样条插值过程中出现的大幅度的振荡现象，从而降低插值误差。

图2 三次样条插值、分段三次厄米特插值以及张力格林样条插值拟合仿真信号上包络结果

从表1可以看出，GSIT 方法无论在IO 指标还是ERE指标都要优于CSI和PCHI方法；PCHI方法虽然能在插值过程中的在一定程度上克服过冲问题，但其插值曲线光滑性差的特点使得分解误差较大。

表1 3种插值方法对仿真信号进行EMD分解的IO 和ERE指标比较

2.2 直接拟合均值曲线的格林样条插值方法

EMD 算法的关键是求取均值曲线，均值曲线生成的不准确将导致信号的EMD 分解结果不准确。经典经验模态分解采用三次样条插值方法进行上、下包络拟和，来求取信号的均值曲线。但是这种方法求取均值曲线需要上、下包络两次拟合，加之拟合曲线和实际包络会存在偏差，两次拟合更会加大这种偏差［10］，随着迭代的进行，这种偏差会不断积累，最终会使信号分解不能得到正确的结果。

为了克服上述这些缺点，本文提出一种基于极值中点的格林样条插值方法来直接拟合均值曲线。该方法通过以下三步来实现：

（1）采用平行延拓法［11］分别得到信号x（t）左右两端的中点。

（2）找出信号x（t）上所有相邻极值点连线的中点，与信号两端的中点组成信号的中点序列。

（3）用张力格林样条函数拟合中点序列作为均值曲线。

这种拟合均值曲线的方法，由于利用了信号的所有极值点，其拟合精度也会更高。为了验证该方法的有效性，以上述仿真信号为例，比较一下两次包络插值拟合的均值曲线和本文提出的方法 （张力参数取0.5）的差异，其差异性仍采用IO 和ERE指标。

从图3可以看出，通过上下包络两次插值求出的均值曲线与直接张力格林样条插值形成的均值曲线，差异性还是很明显的。通过均值曲线穿过中点的情况来看，后者的误 差 还 是 很 小 的，其IO 和 ERE 指 标 仅 为0.0181和0.0223。

2.3 实际信号分析

图4是电机轴承加速度数据，轴承型号是6326－C3，采样频率fs＝25600 Hz，采样时间1S。

图5分别是CSI、PCHI方法和本文方法拟合的均值曲线 （截取信号中0.022s～0.225s 段表示，张力参数取0.6）。CSI方法在部分相邻极大值点间出现剧烈振荡现象，其均值曲线与极值中点偏差较大。PCHI方法曲线光滑性较差，拟合的效果一般。GSIT 方法直接对极值中点进行插值，拟合的均值曲线与实际信号均值曲线最为接近。从表2可以看出，PCHI方法的IO 指标高达0.2561，分解出的固有模态函数正交性很差，这说明了PCHI方法为了保持相邻极大值点 （或极小值点）间插值曲线的单调性，失去了信号波动的本质，从而导致分解误差较大。

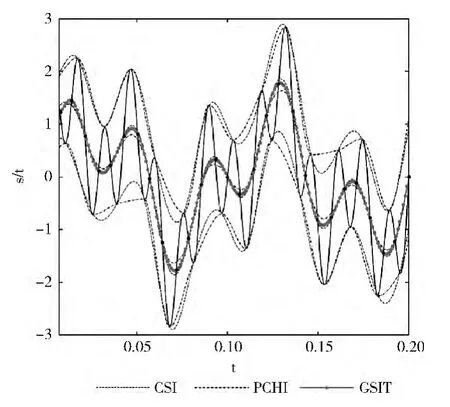
图3 三次样条插值、分段三次厄米特插值和本文方法拟合仿真信号均值均线的结果

图4 电机轴承加速度时域波形

图5 三次样条插值、分段三次厄米特插值和本文方法拟合实际信号均值均线的结果

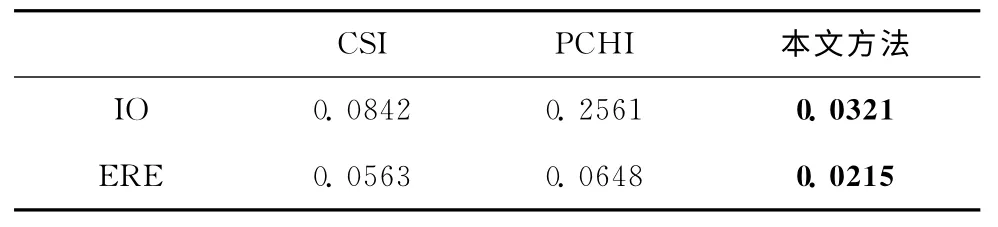
表2 3种插值方法对实际信号进行EMD分解的IO 和ERE指标比较

3 关于张力参数的选取问题

格林函数的加权系数αj是通过求解数据点的线性方程组获得，线性方程组的稳定性很大程度上会受到数据分布的影响。当数据的最大与最小距离值之比很大时，线性系统往往会不稳定［12］。如果数据点分布比较均匀时，线性系统会趋于稳定。通过实验发现，张力参数的取值对线性系统的稳定性有很大影响。当张力参数取值增大时，线性系统特征值的衰减速率明显变慢，系统会更加稳定，但t的取值不能无限增大，当t＝1时，格林函数插值就蜕变为线性插值。所以张力参数的取值一般设定为0.5≤t≤0.7，这样既可以满足分解误差要求，又可以兼顾系统稳定性要求。图6是张力参数t＝0.1和t＝0.7时特征值的衰减曲线，其特征值的最小幅度相差两个数量级。

图6 特征值衰减速度在张力参数为t＝0.1和t＝0.7的比较

4 结束语

针对现有CSI方法存在的问题，本文提出了一种基于张力格林样条的均值曲线插值方法，它在保证插值曲线光滑性的基础上，可以在一定程度上克服CSI方法出现的过冲现象，同时基于极值中点的一次插值也能进一步降低信号分解的误差。仿真信号和实际信号的分析结果也说明了该方法的有效性。但是，对于较长的复杂数据，会碰到大量非规则分布的极值点，由于极值点数增加，对应加权参数的线性方程组求解需要较长时间。如果引入分段格林样条插值［13］，不仅可以减少计算时间，同时也会改变极值点分布的均衡性，有利于提高插值结果的稳定性，这也是后续工作的一个重点。

［1］Huang N E，Shen Z，Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis ［J］.Proceeding of Royal Society，1998，454 （1971）：903－995.

［2］ZHONG Youming，JIN Tao，QIN Shuren.New envelope algorithm for Hilbert－Huang transform ［J］.Journal of Data Acquisition ＆Processing，2005，20 （1）：13－17 （in Chinese）.［钟佑明，金涛，秦树人.希尔伯特黄变换中的一种新包络线算法 ［J］.数据采集与处理，2005，20 （1）：13－17.］

［3］LONG Sisheng，ZHANG Tiebao，LONG Feng.Causes and solutions of overshoot and end swing in Hilbert－Huang transform ［J］.Acta Seismologica Sinica，2005，27 （5）：561－568 （in Chinese）.［龙思胜，张铁宝，龙峰.希尔伯特—黄变换中拟合过冲和端点飞翼 的 原 因 及 解 决 办 法 ［J］.地 震 学 报，2005，27 （5）：561－568.］

［4］Chen Qiuhui.A B－spline approach for empirical mode decompositions［J］.Advances in Computational Mathematics，2006，24 （1－4）：171－195.

［5］ZHU Weifang，ZHAO Heming，CHEN Xiaoping.A leastlength constrained envelope approach for EMD ［J］.Acta Electronica Sinica，2009，40 （9）：1909－1912 （in Chinese）. ［朱伟芳，赵鹤鸣，陈小平.一种最小长度约束的EMD 包络拟合方法 ［J］.电子学报，2009，40 （9）：1909－1912.］

［6］Wessel P.Interpolation using ageneralized Green’s function for a spherical surface spline in tension ［J］.Computer ＆Geosciences，2009，36 （6）：1247－1254.

［7］XIA Jizhuang.An application of biharmonic spline interpolation to integration of logging and seismic data［J］.Oil ＆Gas Geology，2010，31 （2）：244－248 （in Chinese）.［夏吉庄.双调和样条内插方法在测井和地震资料整合中的应用 ［J］.石油与天然气地质，2010，31 （2）：244－248.］

［8］XU Feng，HE Rizheng，ZHANG Guibin.Green’s functionbased interpolator and its application ［J］.Progress in Geophysics，2013，28 （4）：1721－1728 （in Chinese）. ［许丰，贺日政，张贵宾.格林样条插值算法及其应用 ［J］.地球物理学进展，2013，28 （4）：1721－1728.］

［9］Wessel P，Becker JM.Interpolation using ageneralized Green’s function for a spherical surface spline in tension ［J］.Geophysical Journal International，2008，174 （1）：21－28.

［10］ZHU Zheng，WANG Yilin，CAI Ping.A method of obtaining the mean curve for empirical mode decomposition ［J］.Journal of Harbin Engineering University，2011，32 （7）：872－876 （in Chinese）.［朱正，王逸林，蔡平.EMD 中的求取均值曲线方法 ［J］.哈尔滨工程大学学报，2011，32 （7）：872－876.］

［11］Wu Z，Huang NE.Ensemble empirical mode decomposition：A noise assisted data analysis method ［J］.Advances in Adaptive Data Analysis，2009，1 （1）：1－41.

［12］Wessel P，Bercovici D.Interpolation with splines in tension：A Green’s function approach ［J］.Mathematical Geology，1998，30 （1）：77－94.

［13］DENG Xingsheng，TANG Zhong’an.Study on two dimensional spline interpolation based on moving Green’s function［J］.Journal of Geodesy and Geodynamic，2011，31 （6）：69－72 （in Chinese）. ［邓兴升，汤仲安.移动格林基函数样条二维插值算法研究 ［J］.大地测量与地球动力学，2011，31 （6）：69－72.］