基于聚类和动态LOD的三维地形建模方法

吴晓彦，顾韵华，张俊勇，杜 杰

（南京信息工程大学 计算机与软件学院，江苏 南京210044）

0 引 言

DEM （digital elevation model）是描述海拔高度分布的一种数据模型，它不但可以在地理空间中完成精确定位，还能对地面特性或者地貌进行空间数字描述，是反映地形特征的有效手段［1］。DEM 数据对于不同地形类型均采用相同密度采样点描述，而大地形覆盖的区域可能包含不同地形特征，既有高程值变化不大的平坦区域，又有高程值差异很大的山丘和山峰地形，因此DEM 的规则格点数据结构直接用于三维大地形建模，将会存在数据大量冗余从而影响地形绘制效率的问题。考虑到三维地形建模中不规则格网 （triangulated irregular network，TIN）具 有 数 据 冗 余少、细节特征刻画充分，且支持层次细节 （level of details，LOD）多分辨率模型提高效率等优点，本文提出一种基于聚类和动态LOD 的三维地形建模方法，将聚类分析引入到对原始DEM 数据的地貌特征提取中，通过DEM 规则格网数据简化为不规则点集构建TIN 不规则格网，从而降低建模的数据量；同时在三维地形建模中基于视点移动采用局部优化算法，并结合细化评价函数，构建动态LOD 多分辨率层次模型，以达到精确反映地形地貌细节特征并提高绘制效率等目标。

1 相关研究

国内外学者对三维地形建模研究主要集中在数据简化和绘制效率提高等方面。文献 ［2－4］分别从地貌特征角度考虑，提出了基于地理信息强度指数确定特征点的方法保证地貌特征结构，通过计算顶点特征度的方法简化网格，根据地势特征提出了自适应分割的简化方法，从而构建出具有真实感的地形。文献 ［5，6］对细分过程中的点，分别采用距离加权函数构造新点实现模型细分，基于克里金插值法进行反向多级细化。文献 ［7］通过改进 “离核”绘制机制，构建可变地形，文献 ［8，9］分别通过平面曲率构建层次模型，通过边误差的判定调整细节模型，文献［10，11］分别通过建立不完全四叉树结构和Hilbert填充曲线提高绘制效率，通过改进基于Bowyer－Watson增量插点内核的Delaunay算法降低了地形网格规模，文献 ［12］提出了基于视点选择的外存调度层次模型，提高了绘制效率。

由以上研究可知，为了保证简化后的地形不发生变化，都将区域特征这一因素考虑进来，如曲率、地势等；为了提高绘制效率，都采用基于LOD 技术的思想，对数据进行分块处理，或通过改进算法降低网格规模，或采用内外存调度策略等。然而存在的不足是，对区域特征的量化计算都比较复杂，忽略了数据特征自身的相似性，对原始数据集和地貌特征之间没有建立自动关联；而分块LOD 方法易产生块间裂缝问题，基于外存的LOD 方法可能会存在调度效率问题等。针对以上存在的问题，本文提出一种基于聚类和动态LOD 的三维地形建模方法，首先对原始DEM 数据集进行K－means聚类分析，将高程值数据集与地貌特征分类关联在一起，实现客观、无干预的区域特征描述；然后，在聚类分析得到的采样点地貌特征附加属性值基础上，对原始DEM 数据进行粗化处理，形成不规则点集，构建Delaunay三角网；最后，在三维地形绘制的视点变化过程中，采用局 部 优 化LOP （local optimization procedure）算法，并结合节点细化评价函数进行有限域内的三角形分裂，同时采用基于无偏估计的克里金 （Kriging）插值法来计算高程值以提高数据精度，从而实现了多分辨率层次模型，精确反映地貌细节特征并提高绘制效率。

2 基于K－means聚类和动态LOD的地形建模方法

本文提出的三维地形建模方法包括数据预处理、构建不规则三角网和建立LOD 多分辨率层次细节模型等3个阶段，如图1所示。在数据预处理阶段，对读取的DEM 高程数据集进行K－means聚类分析，在采样点和地貌特征分类之间建立关联。然后，根据每一个点的分类值，进行原始数据集的粗化处理，建立不规则三角网。最后采用LOP算法进行局部优化处理并采用克里金法计算插入点的高程值，从而动态生成多分辨率地形模型。与通常的静态生成LOD四叉树结构不同，本文的LOD 多分辨率层次细节模型是在三角形分裂的过程中动态生成的，并采用栈结构表示。

图1 地形建模流程

2.1 基于K－means的地貌聚类分析

地貌是指地面高低起伏的自然状态，地貌特征的表达决定了构建三维地形的真实度。地貌通常划分为平原、丘岭或山峰等类型，不同地貌细节程度差异较大，山峰因其海拔高度局部剧烈变化，细节特征比较丰富，而平原由于其相对比较平稳，具有较少的细节特征，丘岭则介于二者之间，因此可以根据建模区域的海拔高度 （相对海拔高度），很容易度量微观区域的地貌特征。本文采用聚类分析方法的K－means法，该算法具有实现简单，尤其是对大数据集执行速度快的特点。通过K－means聚类分析方法，在高程值数据集合中寻找具有同类属性的数据集合，那么每一类划分中就反映了该区域的地貌特征。

K－means聚类方法是基于样本间相似性度量的间接聚类方法，它把n个对象的集合分为K 簇，采用一个中心点的值来表示该分类的值，簇内的相似度高，而簇间相似度低。设给定m 个样本为｛x（1），…，x（m）｝，该算法过程如下：

步骤1 随机初始化K 个质心 （cluster centroids）为μ1，μ2，…，μk∈Rn；

步骤2 重复下面过程，直到J（c，μ）函数收敛。

（1）对于每一个样本i，计算其属于的类

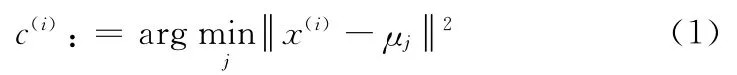
（2）对于每一个类j，重新计算该类的质心

其中，畸变函数 （distortion function）为

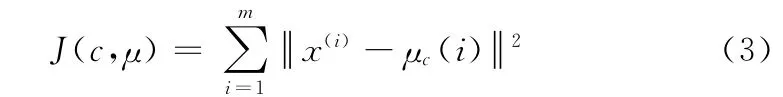
畸变函数J 定义了样本x（i）到对应质心c（i）的距离平方和，K－means收敛即是最小化J 函数的值。每一次调整都要做两步操作，首先保持质心不变，调整每个样本的属类得到J 函数的最小值；保持属类不变，调整质心得到J 函数的最小值。经过两个单调递减过程反复处理，该函数值将达到最小，意味着μ 和c 同时收敛。K 是分类数，c（i）是样本i所属的分类。

根据地貌分类，本文将相应DEM 高程数据代表的地貌划分为高山、丘岭和平原三大类，采用K－means聚类分析方法计算出每个分类的中心值。分别以S1 （平原），S2（丘岭），S3 （高山）表示3类地貌，设每一分类的中心值分别为：δ1、δ2和δ3，现作如下定义：

定义1 对于任意采样点pi的高程值h，存在一个阈值φj（j＝1，2，3），使︱h－δj︱＜φj，而不存在︱h－δm︱＜φm（m＝1，2，3且m！＝j）且︱h－δn︱＜φn （n＝1，2，3且n！＝j，n！＝m）成立，那么点pi∈Sj，则称pi点是Sj地貌的。

定义2 当pi∈Sj （j＝1，2，3）时，定义pi地貌属性为j，记为C（pi）＝j。

例如，当pi∈S2 时，称pi是S2 地貌的，即丘岭地貌；其C（pi）＝2，即该pi点的地貌属性为2。

该算法能够保证同一聚类中的点具有较高的相似性，而不同划分中点的相似度较小，因此每一个集合中的点就描述了一类地貌特征。通过对高程值数据集的分类，为每一个采样点关联一个地貌特征分类属性值。在粗化过程中可依据其微观地貌特征不同，采取不同的策略实现模型数据的简化，如S1区域则可以适当删除点，也满足地形细节特征的表达，其它区域则可适当简化满足细节表达要求。

2.2 网格模型粗化处理

通过对高程数据的聚类分析，规则网格中的每一个采样点均可按照定义1和定义2，得出其所属地形微观区域特征，以及地貌属性C（pi）的值。在此基础上，对DEM 高程数据进行简化，即依据每个点的地貌特征分类属性值，对原始数据集进行粗化处理。粗化处理策略为剔除与邻近点地貌属性值相同的点。剔除点一般限于C（pi）＝1的地形区域点，即选择平原区域采用粗化处理降低建模数据量。若精度要求较低，亦可对C（pi）＞1的区域点适当粗化。

具体计算过程如下：设原始数据集为R，对其中的每个采样点pi，分别计算与pi相邻的上 （pt）、下 （pb）、左（pl）、右 （pr）4个点的地貌属性C 值，若C（pi）＝1且与邻近的4个点之一的地貌属性值相同，则将当前点pi剔除。粗化处理后的数据集记为R1，则此时R1中数据网格已不是规则结构。调整阈值φ1、φ2、φ3，可以找出更多满足定义1的点集属于S1，即该粗化处理过程可以重复多次。每一次的处理数据集分别记为R2、R3……Rn，数据集将越来越小，数据冗余将降低。若按此方法调整C（pi）＞1的采样点，则可进一步简化数据，但可能会丢失山丘或高山的地貌特征，所以在建立初级层次模型精度要求不高时可考虑调整C（pi）＞1的采样点。由于粗化处理中保留的点不再具有规则网格特性，因此粗化处理后的数据集将构成不规则点集。对形成的不规则点集构建Delaunay 三角网，即可生成TIN 模型。

2.3 LOD层次细节模型的建立

在三维地形绘制中的视点变化过程中，随着视点与地形的距离拉近，需要更高精度的高程数据，因此需要建立LOD 多分辨率层次细节模型。构建LOD 多分辨率层次细节模型的过程如图2所示。经过粗化处理所构建的不规则三角网即为层次模型LOD 的根，其所在的层次用0表示，其下一层用1表示，依此类推。由第i （i＝0，1，…）层向第i＋1层转换的过程中，根据节点细化评价函数，对局部三角形进行分裂，重新生成具有丰富细节的三角网，细化过程中采用克里金法确定新点的值，使局部区域更精确的展现出来。

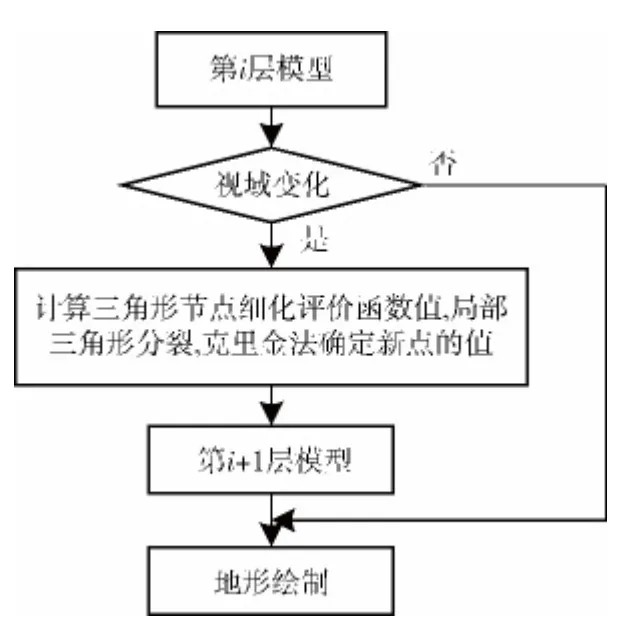
图2 层次细节模型建立过程

2.3.1 节点细化评价函数

三维地形是基于视点进行区域绘制的，在视点变化过程中，视点与地形距离拉近，更多地形细节将展现在视野中。而在视点距模型由远到近的过程中，低分辨率的模型需要逐层细化，满足视觉要求。因此，需要根据地貌细节特征来进行局部地形的优化。局部优化算法通常依据节点细化评价函数来进行。多数情况下节点细化都是针对规则网格的，其节点细化评价函数也主要针对常用的LOD 四叉树结构，对节点细化评价准则的定义分别考虑了视距、地形的特征及该区域的能量函数等。而本文是基于不规则格网的细分，上述评价函数不再适用。因此本文考虑不规则网格特点，考虑地貌属性值、视距及不规则地形区域等要素，定义节点细化评价函数F如式 （4）所示

式中：C（pi）——三角形3 个点地貌特征属性平均值，l——三角形距视点的距离，d——三角形地块的最大边长，在漫游的过程中根据观察者视点位置移动实时计算更新。

节点细化评价函数给出了进行三角型分裂操作的条件，当F＜1时，对三角形进行分裂操作；当F≥1时，该三角形仅进行绘制，不进行细分操作。

2.3.2 局部优化算法和三角形分裂

（1）局部优化算法

不规则Delaunay三角网中的每一个三角形均满足空外接圆的性质，而当构建层次LOD 模型时，当前层次中的一系列三角形需要分裂，构成有丰富细节的三角网，将会出现三角形不再满足空外接圆性质的情况。因此需要进行局部优化处理。本文采用Lawson设计的局部优化算法对已有的三角形进行分裂操作［13］，算法基本原理如图3所示。

图3 局部优化

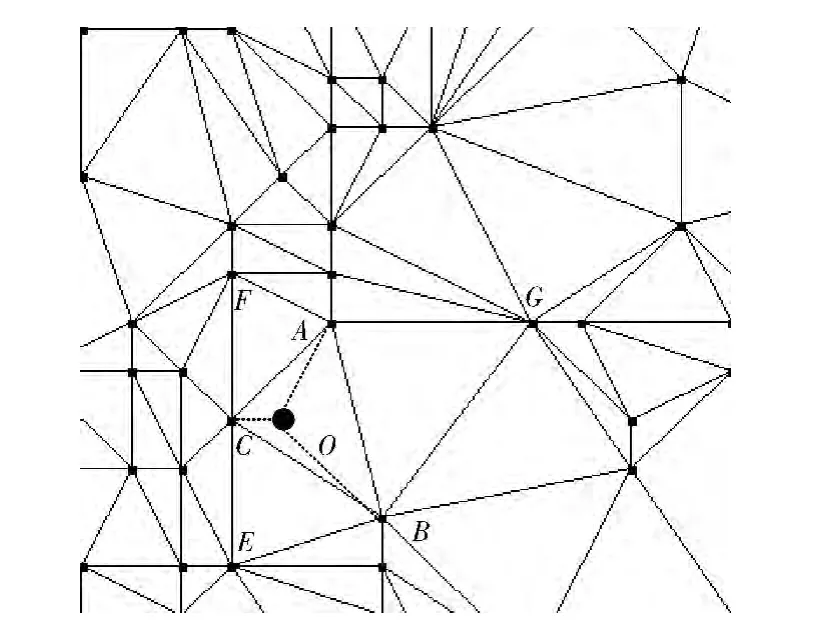
图4 三角形分裂

图4中，若ABC 是待拆分的三角形，因A、B、C 是原始采样点，在三角形ABC 内必包含若干剔除点，根据点的坐标数量关系可以在该三角形内还原出一个点O，点O分别与点A、B、C 连接形成3 个新三角形。根据LOP 局部优化原理，对每一个新三角形进行局部优化处理。如AOB，考察与AB 共边的两个三角形是否满足空外接圆准则，不满足则调整与AOBG 四边形的对角线为OG，再递归调整与AOG 共边为AG 组成的四边形、与OBG 共边为BG的四边形；其余三角形做相同调整操作。经过有限次局部调整，即可形成下一层的Delaunay三角网。

2.3.3 相关数据结构及操作

为了便于层次模型建立，本文采用栈结构存储LOD 细节层次模型，定义以下数据结构。

图3 （a）中ADC 和AEC 是一个Delaunay三角网，B是插入三角形内部的点，可以看出ADC 空外接圆性质被破坏。根据局部优化算法调整ABCD 四边形的对角线AC→BD，此时四边形的两个三角形重新构成Delaunay三角网。

（2）三角形分裂

当计算出的节点细化评价函数F＜1时，需进行三角型分裂。图4是一个三角形分裂过程。

设置两个栈tris＿add和tris＿delete，分别保存新增三角形和删除的三角形。三角形分裂操作过程中，使用LOP（）优化函数，对新产生的三角形递归地优化为Delaunay三角网。在此过程中，上一层的三角形被删除的同时，需记录在栈tris＿delete中，目的是方便回溯，快速恢复上一层的模型；同样，新增加的三角形也记录在tris＿add栈中。

2.3.4 克里金插值确定分裂点高程值

当三角形在视点区域内进行分裂时，需要确定分裂点的高程值。本文采用基于无偏估计的克里金 （Kriging）法计算高程值，该方法原理参见文献［14］。插值公式如下所示

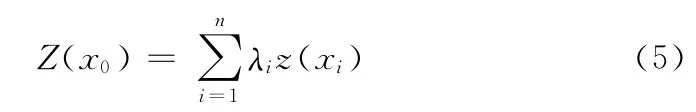
式中：Z（x0）——待估算值，xi（i＝1，…，n）为x0周围的区域观测点，z（xi）——观测值，λi是区域化变量z（xi）的权重，用来表示样本的观测值z（xi）对估算值Z （x0）的贡献程度。系数λi由式 （6）所示方程组求得

式中：γ（xi，xj）是Z 在采样点xi和xj之间的半方差；γ（xi，x0）是Z 在采样点xi和估算点x0之间的半方差；φ是极小化处理时的拉格朗日乘数。由式 （6）可组成n＋1阶线性方程组，求解式 （6）所示线性方程组可得n 个加权系数λi和拉格朗日算子φ。求得各λi值和φ 值后，由式（5）便可得出x0点的估值Z（x0）。

3 实验与分析

为检验本文方法的有效性，从数据简化率、地形特征保持和层次化模型的绘图效率三方面开展实验。所有实验数据均采用SRTM 高程数据作为制作地形数据来源，它是由等间距的规则网格构成，分辨率为90m （0.00083333°×0.00083333°）。在 建 模 中，采 用Visual C＋＋2010 和OpenGL为基础平台，运行环境为Windows 7／32位，处理器Intel Pentium Dual Cpu1.6GHZ，显卡1GB，内存2GB，硬盘120GB。

3.1 不同地形简化率对比实验

选取江苏中部 （平原多，山地少）、河南西部 （山区多，平原少）、云南西南部 （几乎全是山脉），进行对比实验。分别选取128×128、256×256、512×512、1024×1024、2048×2048大小的地块进行测试，其中简化率定义为：（N－P）／N，P 为参与建模的采样点数，N 为原始数据集采样点数。表1给出了对不同地形的数据简化率。

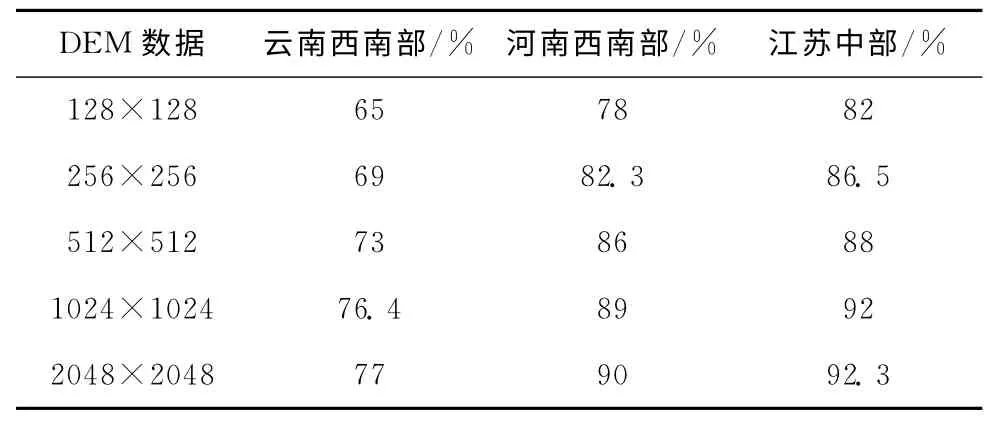
表1 不同地形类型本文方法的简化率

由实验结果可知，本文方法对以平原为主区域的数据简化率最高，表明该区域数据冗余度高，进行数据简化效果最为明显。而对于山区和平原混合的地形类型，简化率低于平原为主的区域，但整体仍然较高的简化率，例如河南西南部地区在2048×2048地块情形下简化率可达90%，表明本文方法对于该类地形仍有较好的简化效果，这是因为本方法中考虑了微观区域的特征，避免了地貌特征点被简化掉。对于山地相对集中的区域，地貌特征比较复杂，数据冗余度最小，但本方法对数据的简化也有一定效果，如云南西南部山区在2048×2048地块情形下简化率仍可达77%。对原始数据集的简化可提高三维地形建模效率。

3.2 地形特征保持测试

为了测试本文方法在不同简化率下地形特征的保持能力，选取具有明显地貌特征的区域进行对比实验。所选区域为经纬度起始点为112.4°、30.8°的200×300 的局部区域，位于河南省的西南部。图5是实验结果，给出了原始地形和该区域不同简化率下地形的三角网模型对比。图5（a）为原始地形三角网模型，图5 （b）、图5 （c）、图5（d）对满足C（pi）＝1的采样点进行了粗化处理所得到的简化率分别为82%、89%、92%的地形三角网模型。实验结果表明，3种简化率下的地形都保留了较多的地貌特征，并且随着简化率的提高，主要地貌特征依然能够很好的保持。例如，图5 （c）为89%简化率的情形，山峰特征保持得很好，山丘特征也被较好的保持了。但92%简化率情形下，山峰特征仍保持得很好，但山丘特征的保持较差。表明本文算法在山峰细节特征上处理较好，而山丘细节特征处理上仍有优化之处。另外，为了保持边界轮廓，避免在粗化中由于过度简化造成地形轮廓丢失，对边界情况进行了特殊处理，限制简化采样点。

图5 原始地形和不同简化率地形三角网模型对比

3.3 三维地形建模效率测试

为了测试本文方法所生成的LOD 多分辨率层次化细节模型的绘图效率，将本文方法与经典基于二叉树的ROAM算法、以及未简化时 （即直接使用高程数据进行三维地形生成）的绘制效率进行对比。ROAM 算法的核心是基于等腰直角三角形、通过二叉树递归分解来构建层次模型。实验区域数据块大小分别为128×128、256×256、512×512、1024×1024、2048×2048，图6为3种方法的绘制效率对比结果。

三维地形建模效率以每秒绘制的帧数 （frame per second，FPS）来度量。图中横轴为地形数据块大小，纵轴为FPS。由图6可见，当数据量超过500×500时，未简化的情形下，进行漫游时出现明显停滞。而本文方法通过网格简化和视域选择绘制的方法，在大地形时仍能实现流畅漫游，传统基于二叉树ROAM 算法［15］相比，效率有所提升。实验说明了对大场景的规则网格数据建模时，对数据简化可以提升性能，通过局部三角形的分裂细化，并保存相邻层次间的数据，也节约了计算时间，避免重复计算从而提升绘图效率。

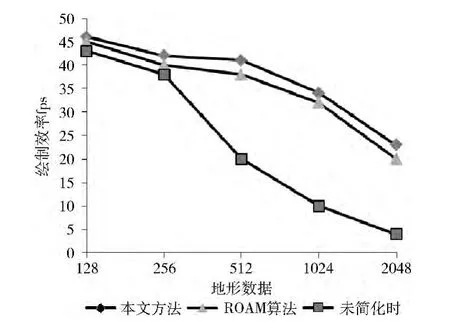
图6 三维地形建模效率测试

4 结束语

在大地形建模过程中，地形模型的简化处理不但能降低程序的复杂性，而且还可提高软件的交互效率。本文通过采用K－means聚类分析法，对原始数据集合进行分类，从而发现数据的相似性，实现了地貌特征的客观、自动分类，完成了采样点与地貌特征属性的关联。在此基础上，实现了微观区域中不同地貌类型的粗化，降低了建模的数据量。同时，在满足精度的要求下改变阈值设置，还可以进一步对数据进行简化。在LOD 层次调整的过程中，根据细化评价函数和局部优化算法实现了层次模型中局部三角形的调整，降低了高分辨率下三角形分裂操作带来的时间消耗，提高了模型更新性能。

［1］TANG Guo’an，LIU Xuejun，LU Guonian.Digital elevation model tutorial［M］.2nd ed.Beijing：Science Press，2010：11－12 （in Chinese）.［汤国安，刘学军，闾国年.数字高程模型教程［M］.2版.北京：科学出版社，2010：11－12.］

［2］DONG Youfu，TANG Guo’an.Research on terrain simplification using terrain significance information index from digital elevation models［J］.Journal of Wuhan University（Information Science Edition），2013，38 （3）：353－357（in Chinese）.［董有福，汤国安.利用地形信息强度进行DEM 地形简化研究 ［J］.武汉大学学报（信息科学版），2013，38 （3）：353－357.］

［3］HUA Haiyang，ZHAO Huaici.Mesh simplification algorithm for terrain model based on feature degree［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2011，23 （4）：594－599 （in Chinese）.［花海洋，赵怀慈.保持地形特征的网格模型简化算法 ［J］.计算机辅助设计与图形学学报，2011，23 （4）：594－599.］

［4］ZHANG Huijie，LU Yinghua，LIU Shuhua.A terrain model simplification method based on adaptive areas division ［J］.Journal of Computer Research and Development，2010，47（1）：53－61 （in Chinese）.［张慧杰，吕英华，刘淑华.一种基于自适应区域分割的地形模型简化方法 ［J］.计算机研究与发展，2010，47 （1）：53－61.］

［5］FU Yanqiang，HAN Huijian.Three－dimensional terrain modeling based on regional feature distance weighting ［J］.Journal of Computer Applications，2012，32 （12）：3377－3380 （in Chinese）.［付延强，韩慧健.基于区域特征距离加权的三维地形建模方法［J］.计算机应用，2012，32 （12）：3377－3380.］

［6］CHEN Xichao，NING Yu.Research on Kriging－based multilevel backward refinement of dynamic terrain modeling ［J］.Computer Engineering and Applications，2013，49 （9）：171－175 （in Chinese）.［陈锡超，宁芋.基于Kriging方法的动态地形反向多级细化研究［J］.计算机工程与应用，2013，49 （9）： 171－175.］

［7］ William E Brandstetter III，Joseph D Mahsman，Cody J White，et al.Multi－resolution deformation in out－of－core terrain rendering ［J］.International Journal of Computers and Their Applications，2011，18 （4）：262－272.

［8］Zarrabeitia LA，Hernández Mederos V.Multiresolution terrain modeling using level curve information ［J］.Journal of Computational and Applied Mathematics，2013，240 （3）：87－98.

［9］Narcís Coll，MaritéGuerrieri.Adaptive simplification of huge sets of terrain grid data for geosciences applications［J］.Journal of Computational and Applied Mathematics，2011，236（6）：1410－1422.

［10］TANG Guiwen，CHEN Xuexia，REN Chao.Research of key technique on virtual reality application based on view－dependent LOD quad tree algorithm ［J］.Computer Engineering and Design，2008，29 （4）：928－930 （in Chinese）. ［唐桂文，陈学霞，任超.视点相关LOD四叉树算法在虚拟现实应用中的关键技术研究［J］.计算机工程与设计，2008，29 （4）：928－930.］

［11］HUANG Zhengke，CHEN Jianjun，ZHENG Yao.Triangulated irregular network based chunk gridding algorithm for terrain rendering ［J］.Journal of Zhejiang University （Engineering Science），2009，23 （10）：1939－1943 （in Chinese）.［黄争舸，陈建军，郑耀.基于不规则三角网的分块地形网格生成算法 ［J］.浙江大学学报 （工学版），2009，23 （10）：1939－1943.］

［12］FENG Jie，ZHA Hongbin.Simplification and view－dependent LOD control for large 3D mesh models［J］.Journal of Computer－Aided Design ＆ Computer Graphics，2006，18 （2）：186－193 （in Chinese）. ［冯洁，查红彬.大型三维网格模型的简化及基于视点的LOD控制 ［J］.计算机辅助设计与图形学学报，2006，18 （2）：186－193.］

［13］XIE Zengguang.Divided－and－conquer algorithm for constructing Delaunay triangulation of planar points ［J］.Computer Engineering and Design，2012，33 （7）：2652－2658 （in Chinese）. ［谢增广.平面点集Delaunay三角剖分的分治算法［J］.计算机工程与设计，2012，33 （7）：2652－2658.］

［14］ZHOU Chenghu，PEI Tao.Principles of GIS spatial analysis［M］.Beijing：Science Press，2011：161－182 （in Chinese）.［周成虎，裴韬.地理信息系统空间分析原理 ［M］.北京：科学出版社，2011：161－182.］

［15］ZHAO Huizhong.Research on theory and visual application of ROAM algorithm ［J］.Geometrics ＆ Spatial Information Technology，2010，33 （5）：124－129 （in Chinese）. ［赵 慧中.ROAM 算法原理及其可视化应用研究 ［J］.测绘与空间地理信息，2010，33 （5）：124－129.］