六自由度振动台台体结构优化设计研究

黄 舟，黄 海

（北京航空航天大学 宇航学院，北京100191）

0 引言

六自由度振动台是重要的振动试验设备，在其工作频率允许范围内可对试件进行多个自由度的振动测试。相比单轴振动台，六自由度台能更准确地模拟实际振动环境，其应用研究越来越受重视[1]。振动台的台体是用于负载和传感器安装的部件，若结构特性偏柔，在高频振动测试时易发生一阶共 振，则会导致对负载响应的测试不准、控制精度显著降低等异常状况[2]。因此，需要提高台体的一阶固有频率，使之位于工作频带以外。为使台体的一阶固有频率高于工作频率，常用加筋的方法[3]来提高台体结构的刚度，这样一来，使得台体结构变重，需要增加振动台的驱动功率。因此，在振动台的设计阶段，有必要进行台体结构的优化，既要满足一 阶固有频率高于工作频率，又要使其质量最小。

台体的结构分析是进行结构优化的基础，为准确求得一阶固有频率需正确地给出边界条件[4]。文献[5-7]虽对六自由度振动台的台体进行了有限元建模，但对边界条件未作明确说明。文献[8]在建模时将边界条件视为自由状态，而在实际工作中，台体结构是通过铰链、作动杆与基座（或地面）进行连接，导致对台体与作动器的连接位置产生沿作动杆轴向的约束。文献[8]还利用ANSYS 软件进行了基于筋板厚度、位置等参数的频率优化设计，属于一阶优化算法。

在关于台体结构的优化研究中，文献[9]明确指出在台体设计时需要对筋板布局、厚度、高度进行分析与优化设计，但缺乏对具体优化过程的描述。文献[10-11]采用传统的反复计算与调整的优化方法，但设计效率很低。文献[12]利用 ANSYS Workbench软件中基于响应面技术的DOE方法对上下板和立板厚度进行了尺寸优化。但由于台体结构包含多种筋板子结构，设计变量较多，所以优化设计时还需要有计算效率更高和适应性更好的优化算法。文献[13]提出了一种二级多点逼近优化算法，通过建立两级近似问题和求解第二级近似问题的对偶问题，使该方法相比传统优化算法在计算效率与收敛速度方面有了很大的提高，因此应用二级多点逼近优化算法将有利于提高台体结构的优化设计。

本文考虑振动台的实际工况，结合二级多点逼近优化算法的收敛迅速稳定的优点，提出一种基于二级多点逼近算法的振动台台体结构的优化方法。首先，分析六自由度振动台的运动工况及各自由度的约束边界条件，建立简化的有限元模型。然后，建立以台体结构中上板、筋板、筋板凸缘的截面尺寸和外形半径大小为设计变量，一阶固有频率和静强度为约束条件，结构质量最小为目标的模型，采用二级多点逼近算法对模型的尺寸进行优化设计，并以人机交互的方式优化外形半径，得到满足约束条件的优化解。最后，依据优化结果完成台体样机的设计，并应用于振动试验测试。

1 台体的有限元模型

1.1 振动台的结构分析

如图1所示，振动台采用具有6-PSU 构型的Hexapod 平台，主要由台体、基座和6 根作动杆组成。其中基座被固定在地基上，作动杆从上到下由二自由度虎克铰、三自由度虎克铰和作动器等构成。台体与6 根作动杆通过3 个连接块相连，通过作动器的伸缩运动实现台体的振动运动。

图1 6-PSU 构型的Hexapod 平台 Fig.1 Hexapod platform with 6-PSU configuration

在确定振动台的构型尺寸后[14]，可得台体与作动杆相连的6 个铰点位置C1到C6，铰点的包络半径为0.5 m，据此尺寸开展台体的设计。

1.2 台体的加筋结构设计与建模

采用航空上广泛使用的整体加筋壁板结构形式[15]，该结构主要包括上板、筋板和筋板顶部的凸缘，如图2所示。考虑到台体与6 个作动杆的连接区域即3 个连接块的位置构成了一个三角形，为使传力路径直接有效，将三角形的3 条边作为主承力筋，其余筋板的周向、径向分布将台体分隔为多个四边形区域。筋板的顶部设计有凸缘，用于提高结构的抗弯刚度。

在MSC.Patran 中建立台体的简化有限元模型，连接区域采用CHEXA8 实体单元，上板结构采用CQUAD4 壳单元，筋板结构及其凸缘分别采用CQUAD4 壳单元与CBAR 矩形截面梁单元，模型共有33 350 个节点，34 068 个单元。

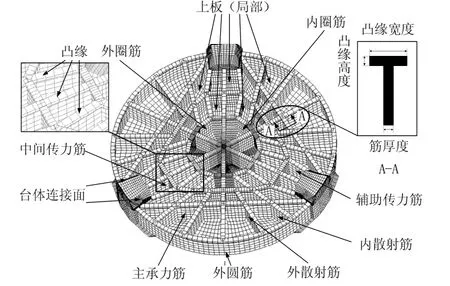
图2 台体有限元模型 Fig.2 Finite element model of the vibration table

1.3 台体边界条件的分析与比较

振动台的6 个作动器在电机驱动下作伸缩运 动使台体产生上下振动。每根作动杆对台体的约束边界如图3所示，作动杆围绕初始位置作微幅振动，当台体处于稳态振动时，其结构的模态应为约束模态而非自由模态，其约束为电机力作用位置处的法向位移。

内筒和杆BC的轴向刚度通常很大，在简化建模时可视为刚体，因此B点为简支点，且C点只能绕B点转动。由于台体运动的振幅很小，在线性分析时，台体连接面上节点只能在垂直于y向的平面内运动。基于上述分析，将台体连接面上的节点平动自由度约束即可。

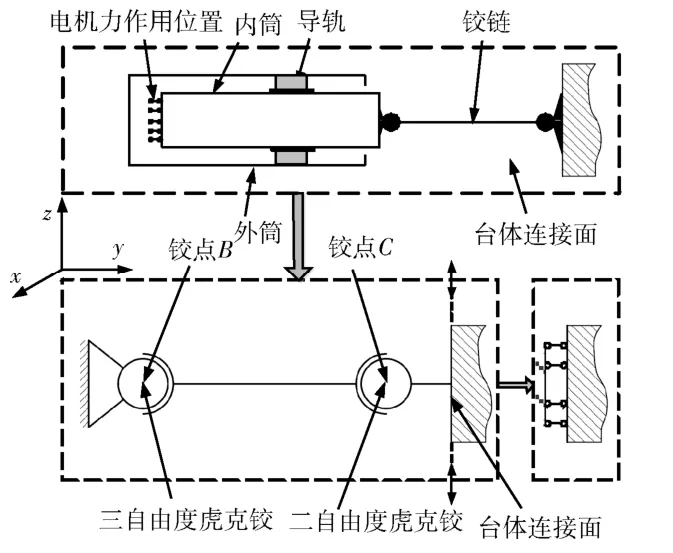
图3 台体在各杆连接面处的边界条件 Fig.3 Boundary conditions in the table’s connecting areas with legs

给定上板厚度（初值为10 mm）、筋的厚度（主承力筋厚度为20 mm，其余筋板厚度为6 mm）、凸缘的宽度（初值为20 mm）和高度（初值为10 mm）等尺寸，台体材料为6061 的铝材，质量为117.9 kg，按上述边界条件进行模态分析，结果显示，台体结构的一阶固有频率为435.2 Hz。

当采用自由边界条件进行模态分析时，结果显示，其一阶固有频率为316.2 Hz。2 种边界条件下的台体结构一阶固有频率相差119 Hz，结合实际情况，台体的结构分析应考虑带约束的边界条件。

2 台体的结构优化设计

2.1 台体模型的建立

振动台在空载时的工作频率范围为5～500 Hz，当安装800 kg 的负载后，能同时承受纵向和横向的过载加速度分别为2g和1g。因此，根据工作频率，要求台体一阶固有频率高于500 Hz，以安装负载后的静强度、刚度作为约束条件，以台体结构的质量最小为设计目标，即优化问题可表达为

式中：X= {x1,x2,···,x n,r}T为优化的设计变量，其中x1,x2,···,xn分别为台体上板厚度、加筋板厚度与凸缘截面尺寸，r为外圆筋的半径；f(X)为质量目标函数；g(X)为设计约束函数，由于静载荷下的强度要求一般为非临界约束[16]，在优化时对该约束条件进行简化，即约束函数只取台体的一阶频率下限，取= 500 Hz；xiL和xiU分别为设计变量xi的下限和上限。

台体的简化有限元模型均将梁单元和壳单元的截面尺寸视为待优化的设计变量，这些设计变量在链化处理时应结合几何对称性。经链化后截面尺寸变量总数为n=86，由于铰点位置已经确定，r可改变台体的外形而不改变连接面的位置，所以台体优化模型中独立的设计变量共计87个。

2.2 二级多点逼近优化算法

采用二级多点逼近优化算法进行优化。式(1)表达的为复杂的隐式问题，若直接对它求解则计算效率很低，为此，需要建立具有高保真度的第一级近似问题表达式，即

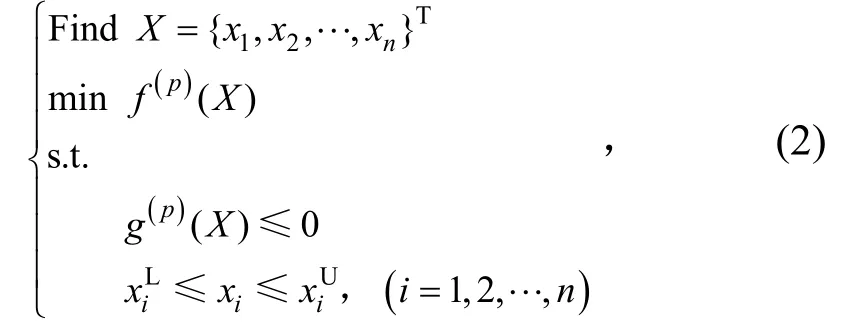
式中：f(p)(X)和g(jp)(X)为第p个优化周期内的目标函数和约束函数的近似函数，由于式(1)中的目标函数f(X)与设计变量之间具有显式对应关系，则有f(p)(X)=f(X)，g(p)(X)为g(X)的近似函数，因而可通过若干已知设计点的临界约束函数值及其导数得到[17]。

在式(2)中，约束函数仍为复杂的非线性显函数，很难写出设计变量和对偶变量之间的显式关系，无法直接使用对偶法求解，还需要采用第二级近似问题来逼近由式(2)表达的第一级近似问题。可先建立第二级近似问题的对偶问题，再通过求解对偶问题得到第二级近似问题的解X*。当X*达到第 二级近似问题的收敛精度ε2时，将X*作为新的设计变量Xp。此时，在Xp处进行结构分析和灵敏度分析，并判断台体结构质量f(Xp)是否满足第一级近似问题的收敛精度ε1。当结构质量f(Xp)满足ε1时，则Xp为原问题(1)的最优解；若不满足ε1，则将Xp增加为已知设计点并重新建立第一级近似问题，进而转入下一周期的优化迭代，直至结构质量满足ε1，此时的Xp为原问题的最优解。

2.3 优化过程与结果

台体结构优化过程分为两个阶段：第一阶段为采用二级多点逼近优化算法对模型的截面尺寸优化，第二阶段为综合尺寸优化和结构分析的结果，以人机交互的方式[18]优化形状变量r，优化设计流程如图4所示。考虑到外圆筋的振型主要表现为扭转与径向振动，应减少半径r以缩短外圆筋的长度，经形状调整、优化后再次进行尺寸优化，直到优化结果满足频率和静强度约束条件。优化后的台体模型如图5所示。

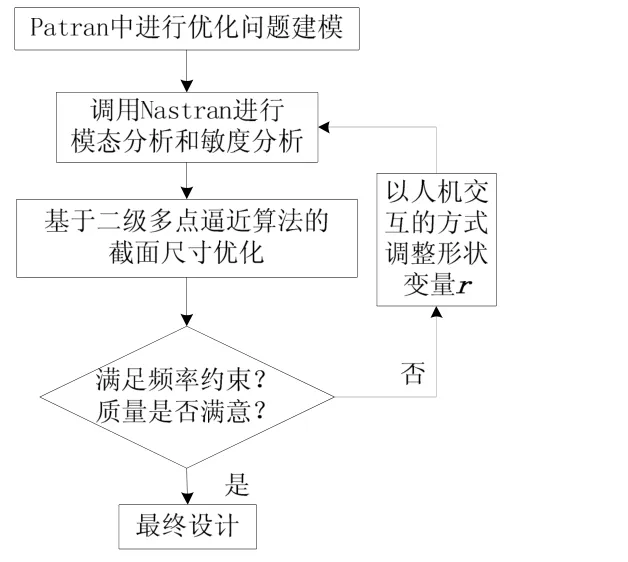
图4 台体优化设计流程 Fig.4 Optimization design process of the vibration table

图5 优化后的台体模型 Fig.5 Model of the table after optimization

对外形优化前和优化后模型分别进行质量优化，优化迭代过程见图6，可以看到外形变量r对优化结果有较大影响。外形优化后的台体质量为90.0 kg，一阶频率为501.7 Hz。由于筋板厚度和凸缘截面尺寸的设计变量简化方法相同，以主承力筋和其上部凸缘为例，设计变量的优化结果见表1。相比外形优化前的模型，其频率提高了66.5 Hz，质量减小了27.9 kg。

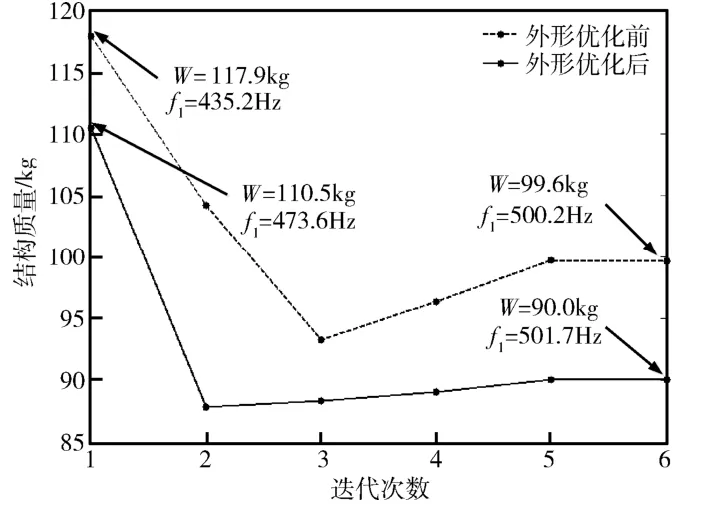
图6 外形优化前后的结构质量优化的迭代曲线 Fig.6 Mass iteration curve before and after shape optimization

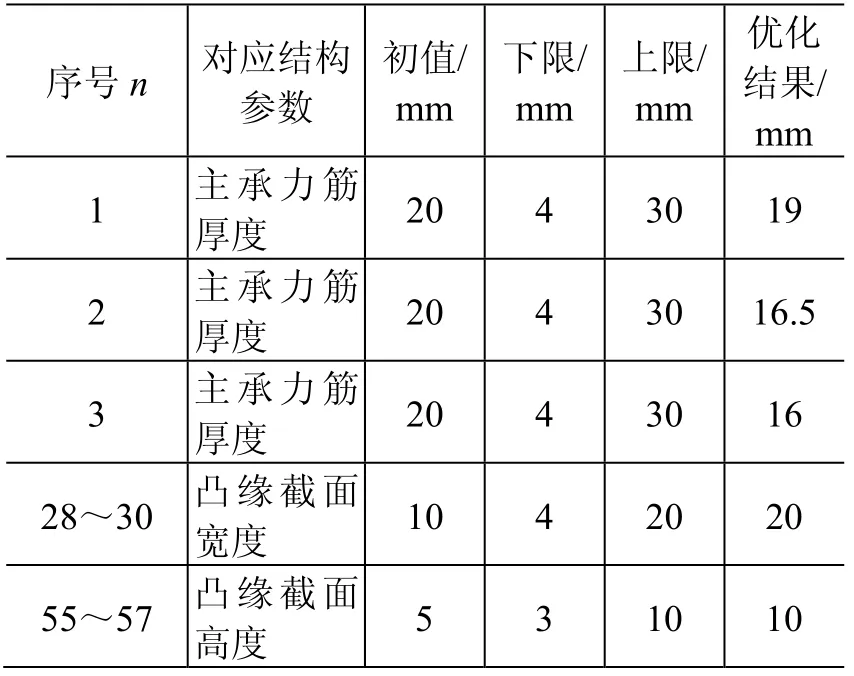
表1 典型设计变量 Table1 Typical design variables

3 基于优化结果的台体样机设计

经外形和质量优化后筋板的厚度与凸缘的截面尺寸一般带有多位小数，在详细设计前应圆整。当相邻筋板或凸缘的尺寸接近时进行归一化处理以便设计和制造，根据圆整后的尺寸在Catia软件中完成台体的详细设计。

由于详细设计后的台体模型与简化模型有所不同，需要验证其是否满足式(1)中的约束条件，故将Catia中的三维模型导入Patran后，再采用CTETRA10单元划分网格，边界条件与简化模型相同。经Nastran的静力学和模态分析求解，在台体上安装有负载且达到所要求的过载工况下其最大Von Mises应力为38.1 MPa，远小于材料的强度极限；最大变形为0.094 mm，均满足静强度和刚度的要求；基频为540.67 Hz，也满足频率要求。

经过静强度、刚度和频率校核后，根据设计模 型的尺寸，采用铝材经整体铣削加工得到台体样机，其总质量为93.6 kg（接近90.0 kg），如图7所示。台体样机已用于振动试验测试，满足了给定频率要求下的轻量化设计要求。

图7 台体结构图 Fig.7 Structure of the vibration table

4 结论

为了满足多自由度振动台台体固有频率高于工作频率和结构质量最小的设计要求，采用二级多点逼近优化算法对台体进行了优化设计，得到以下结论：

1）采用约束边界所建立模型的固有频率比自由边界高出119 Hz，结合实际情况，二级多点逼近优化中优化建模应采用约束边界；

2）优化后的台体模型与用于优化的简化模型相比，一阶固有频率接近，表明上板、筋板和凸缘等结构的简化建模是合理有效的；

3）台体的结构优化属于工程问题，采用基于二级多点逼近算法的结构优化方法，从优化迭代曲线可以看出优化计算收敛迅速且稳定。优化后的台体模型频率提高了66.5 Hz，而质量降低了27.9 kg，效果明显，从而验证了该优化方法的有效性。

（References）

[1] 韩俊伟,张连朋.多自由度振动台的发展与控制技术[J].液压与气动,2014(1): 1-6 Han Junwei,Zhang Lianpeng.The development and control technology of multi-DoF shaker[J].Chinese Hydraulics ＆Pneumatics,2014(1): 1-6

[2] Clark A J.Dynamic characteristics of large multiple degree of freedom shaking tables[C]//Proceedings of the Tenth World Conference on Earthquake Engineering.Madrid,Spain,1992: 2823-2828

[3] 陈晓利,盛美萍.多加筋圆柱壳体振动特性的导纳法研究[J].振动与冲击,2007,26(4): 133-135 Chen Xiaoli,Sheng Meiping.Vibrational characteristics of a multi-beam-stiffened cylinder shell by mobility analysis[J].Journal of Vibration and Shock,2007,26(4): 133-135

[4] Forsberg K.Influence of boundary conditions on the modal characteristics of thin cylindrical shells[J].AIAA Journal,1964,2(12): 2150-2157

[5] 陈良.多轴振动试验台结构设计与分析[D].哈尔滨: 哈尔滨工业大学,2010: 15-19

[6] 许益明.基于六维加速度传感器的六维冗余振动台技术研究[D].上海: 上海交通大学,2009: 40-44

[7] 乔涛.冗余驱动振动台内力分析与控制[D].哈尔滨: 哈尔滨工业大学,2008: 30-33

[8] 王东升,刘青林,张志旭,等.多轴振动台台面频率优化[J].航天器环境工程,2008,25(4): 351-354 Wang Dongsheng,Liu Qinglin,Zhang Zhixu,et al.Frequency optimization of multi axis shaker’s table[J].Spacecraft Environment Engineering,2008,25(4): 351-354

[9] Popovitch A,Piret G,Decobert F.New QUAD multishaker at ESA-ESTEC[C]//Proceedings of the 24thAerospace Testing Seminar 2008.California,USA,2008: 235-246

[10] 苏嵩,陈红光,郁林聪.高频电液振动台用台面的性能分析及优化设计[J].液压与气动,2009(2): 19-21 Su Song,Chen Hongguang,Yu Lincong.Design optimization and characteristic analysis of high frequency electro-hydraulic vibration generator[J].Chinese Hydraulics ＆Pneumatics,2009(2): 19-21

[11] 夏天凉,王金娥,卢华强,等.电动振动台附加台面的结构分析及其优化设计[J].苏州大学学报: 工科版,2011,31(3): 49-54 Xia Tianliang,Wang Jin’e,Lu Huaqiang,et al.Structural analysis and optimal design of electro- dynamic vibrator appending table[J].Journal of Soochow University: Engineering Science Edition,2011,31(3): 49-54

[12] 周兴华.共振式重载液压振动台结构优化及模型控制研究[D].长春: 吉林大学,2014: 53-67

[13] Huang H,Xia R W.Two-level multipoint constraint approximation concept for structural optimization[J].Structural Optimization,1995,9(1): 38-45

[14] 夏禹,黄海.Hexapod 平台参数设计优化[J].航空学报,2008,29(5): 1168-1173 Xia Yu,Huang Hai.Design optimization for Hexapod platform parameters[J].Acta Aeronautica ET Astronautica Sinica,2008,29(5): 1168-1173

[15] 曾元松,黄遐.大型整体壁板成形技术[J].航空学报,2008,29(3): 721-727 Zeng Yuansong,Huang Xia.Forming technologies of large integral panel[J].Acta Aeronautica ET Astronautica Sinica,2008,29(3): 721-727

[16] 周志成,曲广吉,黄海.某卫星平台多结构工况下的 优化设计[J].北京航空航天大学学报,2009,35(7): 821-823 Zhou Zhicheng,Qu Guangji,Huang Hai.Design optimization of a satellite platform considering multiple structural cases[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(7): 821-823

[17] 黄海,夏人伟.复杂结构优化设计的二级多点逼近方法[J].航空学报,1994,15(7): 780-786 Huang Hai,Xia Renwei.Two-level multi-point approximating method for optimal design of complicated structures[J].Acta Aeronautica ET Astronautica Sinica,1994,15(7): 780-786

[18] 袁家军,陈珅艳,黄海,等.基于Patran/Nastran 的结构优化系统的工程应用[J].北京航空航天大学学报,2006,32(2): 125-129 Yuan Jiajun,Chen Shenyan,Huang Hai,et al.Engineering applications of structural optimization system based on Patran/Nastran[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(2): 125-129