应用经验模态分解的箱型结构裂纹诊断方法
谢一村,樊世超,杨艳静
(北京卫星环境工程研究所,北京 100094)
0 引言
航天器结构故障诊断是一个重要的课题。现有航天器振动试验中,一般采用特征级结构响应曲线法进行结构故障诊断。具体说来,就是对比振动试验前后两次特征级结构响应数据,根据频率漂移和响应放大来判断振动试验后是否发生结构故障[1]。这种方法只能用作定性判断,并不能确定故障的位置和故障类型,以及是否需要做结构改进等。这些因素往往需要人工判断,有时还需要进行开舱检查,耗费大量的时间、人力和物力。另外,这种方法主要参考了数据在频域方面的特征,并未充分考虑数据在时域上的特性。
虽然主动监测方法[2-7]和模态分析方法[8](包括 应变模态法[9])通过模态都能较为有效地识别结构的故障,但是对结构振动信号进行时频处理,仍然是结构故障诊断中最有效、最常用的方法。结构故障振动信号在很多情况下表现为非平稳特征,为了了解信号频谱随时间变化的情况,须采用时频分析处理非线性、非平稳信号。较为常用的时频处理方法有短时傅里叶变换、Wigner-Ville 分布和小波变换等。北京卫星环境工程研究所已经开展了对航天器结构故障诊断的相关研究:王婉秋采用小波分解系数为基础的能量范数作为特征向量,对典型的小卫星箱式结构进行了故障诊断[10];朱建斌建立了一种加权小波灰度矩阵方法,对航天器结构振动谱图进行了特征提取[11]。这些方法主要是基于小波变 换,还未使用到其他时频处理方法。
1998年,美国航空航天局的Norden E.Huang等提出了一种称为Hilbert-Huang 变换的信号处理 方法[12-13]。该方法把时域信号进行经验模态分解(empirical mode decomposition,EMD),得到一组固有模态函数(intrinsic mode function,IMF);再对IMF 进行Hilbert 变换,获得信号的Hilbert 边际谱和Hilbert 能量谱等,以实现降噪和谱分析的要求。EMD 方法是Hilbert-Huang 变换中的关键。经过对比发现,Hilbert-Huang 变换与其他时频处理方法相比,更适用于处理非线性、非平稳信号[14-16]。
箱式结构多用作小卫星的主结构,也常作为大型航天器的次结构,结构形式变化多、应用广泛。为获得航天器结构故障的更多信息,本文以一个两层箱型结构为研究对象,应用EMD 方法对该结构振动响应的时域数据进行分析,从IMF 角度分析结构完好和有裂纹状态的响应。
1 经验模态分解的基本应用
IMF 是EMD 方法中一个重要的概念。IMF 应满足2 个条件:1)在整个时间范围内,极值点和过零点的数目相等或者最多只差1;2)在任意一点,由局部最大值定义的上包络和由局部最小值定义的下包络的均值为0。EMD 就是把原始信号x(t)分解成n个固有模态函数ci(t)(i=1,2,…,n)和一个余项rn。
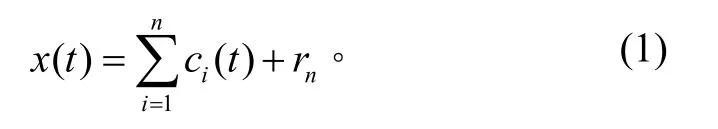
编制EMD 过程的MATLAB 程序,考察式(2)中的原始信号x(t)。该信号由频率分别为10、30 和100 Hz 的3 个正弦信号组成,采样频率为1000 Hz,采样时间为1 s。EMD 分解过程如图1所示。

EMD 就像一个高通滤波器,将原始信号从高频到低频依次分解,最后得到余项。对该信号分解后得到4 个IMF 分量和1 个余项。其中第1 个IMF分量正好对应100 Hz 的正弦信号,第2 个对应 30 Hz 的正弦信号,第3 个对应10 Hz 的正弦信号。至于第4 个IMF 分量和余项,产生原因可能是端点效应造成的。总的来说,通过经验模态分解得到了原始信号的组成分量,验证了程序设计的有效性。
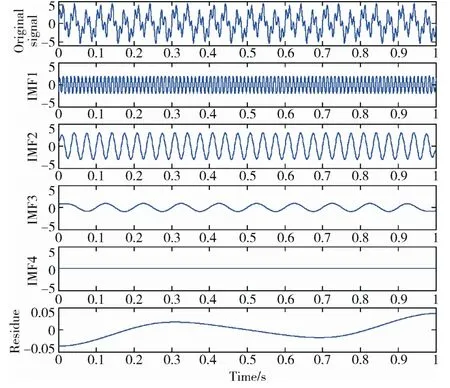
图1 原始信号及其分解结果 Fig.1 Original signal and its sifting results
2 试验件仿真研究
以两层箱式结构作为研究对象,研究结构中板的故障诊断问题。试验件结构如图2所示,其材料特性参数见表1,模型为底端固定。
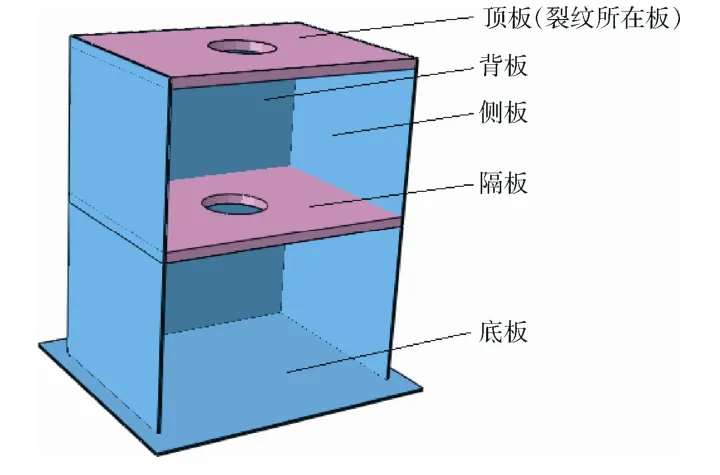
图2 两层箱式结构试验件示意图 Fig.2 The schematic diagram of test specimen model with a two-layer box shape

表1 试验件材料特性 Table1 The material parameters of the test specimen
采用MSC 公司的Patran2011 软件建模和Nastran2011.1 工具进行分析。试验件的有限元模型如图3所示。为了使模型更加接近于真实,建模中采用了与实际结构相同的角片进行连接,如图4所示。

图3 试验件有限元模型 Fig.3 Finite element model of the test specimen

图4 角片模型位置示意图 Fig.4 The positions of connecting pieces
试验件底端固支,分别计算了结构完好(工况01)和顶板中心开孔处沿y向有一裂缝(工况02)两种工况的前4 阶模态,数据如表2所示。两种工况下一阶、四阶振型对比见图5。
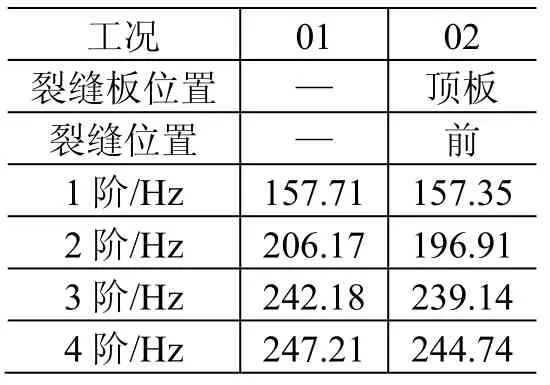
表2 两种工况前4 阶模态频率 Table2 The natural frequency comparison of two cases

图5 工况01(左)和工况02(右)分别对应的1 阶和 4 阶模态振型对比 Fig.5 Comparison of 1st mode and 4th mode between case 01 and case 02
可以看出,与工况01 相比,工况02 的固有频率和振型变化非常小,从模态角度很难判断结构是否存在故障。因此需要采用一种新的方法,以获取判断故障的更多信息。
3 试验实施和结果分析
3.1 试验方案
试验件结构见图6,箱体侧板与底板之间采用焊接连接,顶板和侧板利用螺栓和角片完全固定。其参数同表1。
设计了2 种状态的试验件,其中:工况01 为完整结构,即顶板中部有开孔但无裂纹;工况02为在箱体顶板有开孔并沿y向有裂纹,如图7所示。试验中的振动加载方向见图3中坐标,试验条件如表3所示。4 个测点布置在顶板4 条边的中点处(见图7),测量每个测点三个轴向的加速度响应。
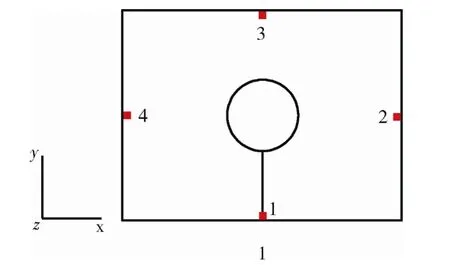
图7 工况02 的顶板结构及测点位置示意图 Fig.7 The schematic diagram of upper board with the position of crack and sensors

表3 x,y,z 方向振动试验条件 Table3 The vibration test conditions in x,y,z directions
3.2 试验结果分析
图8是工况01和工况02的部分测点频响曲线对比。从频响数据可以看出,工况02和工况01的频响曲线比较相似,但和工况01相比,工况02的频响曲线仍然出现了一定的频率漂移和响应放大,据此可 判断结构发生了变化,但是难以获得更多有关故障的信息。

图8 两种工况的测点1在x主振方向和测点4在y主振方向 的频响曲线对比 Fig.8 Comparison of frequency response between sensor 1 in x direction input and sensor 4 in y direction input under case 01 and case 02
由于端点效应、能量泄漏等原因,分解到较高阶的IMF并没有实际的物理意义,只需分解较少层数就能取得良好的分析效果。由于正弦时域数据量较大,为了在保证分析效果的前提下减少计算量,这里只分解到前4阶的IMF,认为第5阶以上即为余项。
图9为两种工况下测点1在x主振方向的时域曲线,可以看出,同一测点在不同工况下的时域数据比较类似。对时域数据的EMD分解过程如图10所示。

图9 两种工况下测点1在x主振方向的时域曲线 Fig.9 Time-domain curves of sensor 1 in x direction input under case 01 and case 02

图10 两种工况下测点1在x主振方向的时域数据EMD 分解过程 Fig.10 EMD processes of time-domain results for sensor 1 in x direction input under case 01 and case 02
将原始振动信号x(t)进行分解得到n个IMF分量c1(t),c2(t),…,cn(t)和余项rn,分别求各个IMF分量和余项rn的总能量Ei,Er,则有
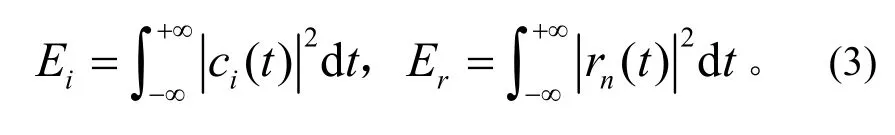
以各分量能量为元素构造标识向量T,则有
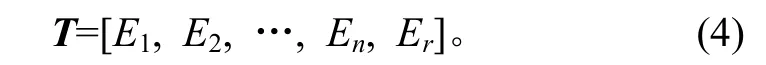
由于能量数值一般较大,需对T进行归一化处理。
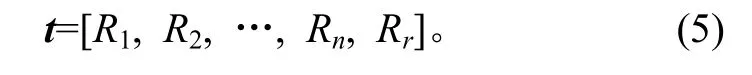

可根据标识夹角α的变化判断结构的故障信息。
对试验得到的正弦振动响应数据进行EMD分解,再进行上述的分析,结果见表4。

表4 工况01 和工况02 的试验数据分析结果 Table4 The analysis results of test data for case 01 and case 02
对于工况02,裂纹沿y方向、并正交于x方向,测点1 距离裂纹位置最近。从表4可以看出,当给试验件x方向主振激励时,测点1 和其余测点相比,其标识夹角α最大;当进行其他方向主振激励时,α则没有明显最大值的特征。
为了验证故障特征提取的有效性,再加工一块沿x方向有裂缝的顶板,如图11所示。这种情况定义为工况03,x,y,z三方向试验条件同表3。试验得到工况03 的振动试验时域数据,用上述方法分析,结果见表5。
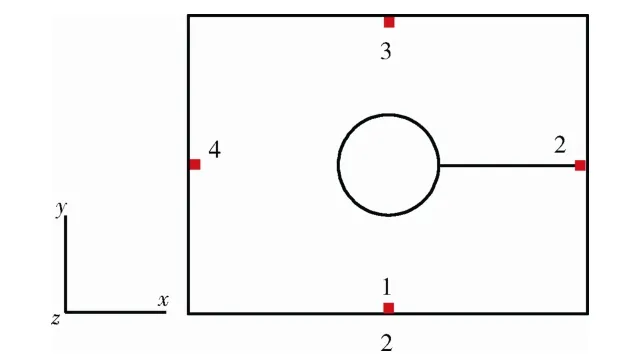
图11 工况03 的顶板结构及测点位置示意图 Fig.11 The schematic diagram of upper board and the positions of sensors for case 03
从表5可以看出:裂纹沿x方向且正交于y方向,测点2 距离裂纹位置最近,当给试验件y方向 主振激励时,则测点2 的标识夹角α最大;当进行其他方向主振激励时,α没有明显最大值特征,验证了故障特征提取的有效性。从以上分析结果可以得到:利用上述的标识夹角α,结合施加给结构的主振方向,可以大致判断出箱式结构中板的裂纹位置和方向。

表5 工况03 试验数据分析结果 Table5 The analysis results for case 03
4 结束语
基于信号处理的航天器结构故障诊断方法(如结构响应曲线对比法)可以判断出航天器结构发生了故障,但是难以获得有关结构故障的更多信息,如故障形式、故障位置、故障程度等。本文先对一个两层箱型结构进行有限元建模和模态分析,分析发现结构有无裂纹对结构的模态振型、模态频率变化较小;又对该结构进行正弦扫频振动试验,虽然结构有无故障的频响曲线有差异,但难以从差异中判断结构故障的信息;将正弦振动扫频响应时域信号进行EMD 分解,利用IMF 能量分量构造标识向量,利用标识向量构造的标识夹角α作为诊断结构故障的指标,结合激励的主振方向可以定量判断出箱型结构中板的裂纹的位置和方向,为航天器结构故障诊断提供了一种新的思路。
(References)
[1] 向树红.航天器力学环境试验技术[M].北京: 中国科学技术出版社,2008: 18-58
[2] 刘江韦,刘镇清.关于用Lamb波的反射对层状复合材料进行无损检测的研究[J].无损探伤,1998,22(1): 34-35
[3] Su Z Q,Ye L.Lamb wave propagation-based damage identification for quasi-isotropic CFEP composite laminates using artificial neural algorithm: Part I: Methodology and database development[J].Journal of Intelligent Material Systems and Structures,2005,16: 97-111
[4] Su Z Q,Ye L.Lamb wave propagation-based damage identification for quasi-isotropic CFEP composite laminates using artificial neural algorithm: Part II: Implementation and validation[J].Journal of Intelligent Material Systems and Structures,2005,16: 113-125
[5] 彭鸽,袁慎芳,徐颖娣.基于主动Lamb 波和小波变换的二维结构损伤定位研究[J].振动工程学报,2004,17(4): 488-493 Peng Ge,Yuan Shenfang,Xu Yingdi.Damage location of two-dimensional structure based on wavelet transform and active monitoring technology of Lamb wave[J].Journal of Vibration Engineering,2004,17(4): 488-493
[6] 孙亚杰,袁慎芳,邱雷,等.基于Lamb 波和相控阵的复合材料损伤识别研究[J].测控技术,2008,27(增刊1): 239-243 Sun Yajie,Yuan Shenfang,Qiu Lei,et al.Research of damage identification for composites based on Lamb wave and phased array technology[J].Measurement &Control Technology,2008,27(sup 1): 239-243
[7] 蔡建,袁慎芳,张逍越,等.Lamb 波双面激励方法及其在近邻损伤监测中的应用[J].南京航空航天大学学报,2010,42(1): 62-67 Cai Jian,Yuan Shenfang,Zhang Xiaoyue,et al.Lamb wave double side excitation and its application in adjacent damage monitoring[J].Journal of Nanjing University of Aeronautics &Astronautics,2010,42(1): 62-67
[8] 杨智春,于哲峰.结构健康监测中的损伤检测技术研究进展[J].力学进展,2004,34(2): 215-223 Yang Zhichun,Yu Zhefeng.Progress of damage detection for structural health monitoring[J].Advances in Mechanics,2004,34(2): 215-223
[9] 朱晓玲,向在喜,胡均安,等.平面薄板结构应变模态分析[J].广西工学院学报,2004,15(1): 31-34 Zhu Xiaoling,Xiang Zaixi,Hu Jun’an,et al.An analysis of strain modality of the level sheet structure[J].Journal of Guangxi University of Technology,2004,15(1): 31-34
[10] 王婉秋.基于小波分析的箱式结构故障诊断研究[D].中国空间技术研究院,2007: 18-34
[11] 朱建斌.航天器振动故障诊断的振动谱图技术研究[D].中国空间技术研究院,2014: 85-101
[12] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis[C]∥Proceedings of the Royal Society: Series A: Mathematical Physical and Engineering Sciences,454(1971).London,1998: 903-995
[13] Pinesa D,Salvinob L.Structural health monitoring using empirical mode decomposition and the Hilbert phase[J].Journal of Sound and Vibration,2006,294: 97-124
[14] 伍小燕.基于时频分析的轴承故障自动检测方法研究[D].苏州大学,2008: 17-26
[15] 向玲,唐贵基,胡爱军.旋转机械非平稳振动信号的时频分析比较[J].振动与冲击,2010,29(2): 42-45 Xiang Ling,Tang Guiji,Hu Aijun.Vibration signal’s time-frequency analysis and comparison for a rotating machinery[J].Journal of Vibration and Shock,2010,29(2): 42-45
[16] 李迎.三种时频分析技术在复合材料无损检测中的应用[J].计测技术,2011,31(6): 1-3 Li Ying.Applications of three time-frequency methods on composite material damage detection[J].Metrology &Measurement Technology,2011,31(6): 1-3

