多轴随机振动试验控制技术研究
邱汉平,冯咬齐,2,樊世超
(1.北京卫星环境工程研究所,北京 100094; 2.北京卫星环境工程研究所 可靠性与环境工程技术重点实验室,北京 100094)
0 引言
在振动环境模拟试验领域,相对于单轴激励振动方式,多轴振动激励能更真实地模拟实际的动力学环境,从而可暴露大型复杂结构在单轴振动激励时不易被发现的缺陷。多轴振动试验技术自20世纪60~70年代出现以来,其应用由初期的地震、汽车、军工等行业逐渐扩展到航空、航天领域[1-4]。在多轴随机振动试验技术中,多轴振动控制既是试验的关键点,也是试验的一个难点。国外开展了大量的多轴振动控制技术研究,并推出了如Spectral Dynamics 公司的Jaguar 及Data Physics 公司的Signal Matrix 等多轴控制软件产品[5]。相比之下,国内却还没有成熟的商用产品问世。通过学习和借鉴国外的多轴控制技术,北京卫星环境工程研究所自主研发了一套多轴随机振动控制系统。
本文在介绍多轴随机振动控制基本原理的基础上,详细分析利用自主研发的控制系统在三轴振动试验台上进行三轴随机振动试验的控制效果。开展多轴振动试验控制技术研究将为深入认识多轴振动模拟试验机理、分析研究和制定多轴振动试验条件等方面提供参考。
1 多轴随机振动控制原理
1.1 系统传递特性辨识
多轴振动试验系统可以描述成如图1所示的多输入多输出系统。

图1 多轴振动试验系统模型示意 Fig.1 Schematic diagram of the model of the multi-axis vibration test system
其中,辨识系统的传递函数是多轴随机振动试验控制的关键环节。多轴振动试验系统同时输入N路低量级的独立随机驱动信号并测量系统在N个控制点上的响应输出信号。假定多轴振动试验系统是线性时不变系统,则系统的输入输出信号在频域内可表达为

式中:Y(f)为N维系统响应矢量;H(f)为N×N维系统传递函数矩阵;X(f)为N维驱动信号矢量。将式(1)两边同时乘以驱动信号矢量的共轭转置,则有
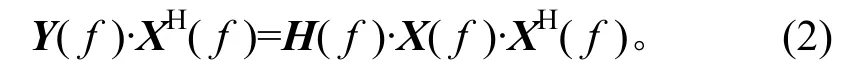
令SYX(f)=Y(f)·XH(f),SXX(f)=X(f)·XH(f),则式(2)可简化为
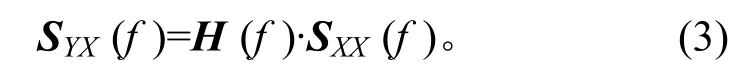
式(3)两边同时乘驱动自谱逆矩阵,则可得系统传递函数为

其中响应与驱动互谱矩阵SYX(f)及驱动自谱矩阵SXX(f)展开后表示为

对于系统在某些频率点处出现奇异或系统为非方阵控制时,频响函数矩阵辨识可用Moore- Penrose 求伪逆的方法进行。
1.2 驱动信号生成
多轴随机振动控制驱动信号生成方法可以按图2方式进行。
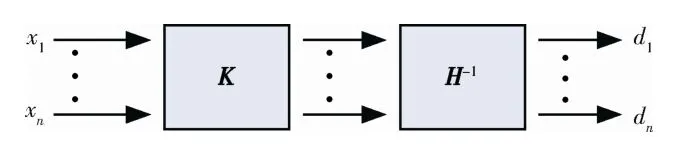
图2 驱动信号生成示意 Fig.2 Schematic diagram of the drive signal generation
图2中,x1,x2,…,xn为独立的白噪声信号,其功率谱密度矩阵为单位矩阵。即设X(f)=[x1(f),x2(f),…,xn(f)]T,白噪声功率谱密度矩阵为Xwn(f),则有
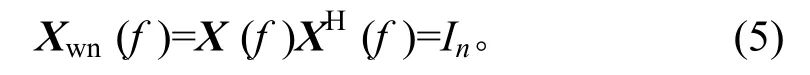
矩阵K(f)为一个下三角矩阵,它通过对正定参考谱矩阵进行Cholesky 分解而得到,则有
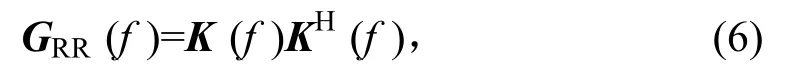
式中:KH(f)矩阵为分解矩阵K(f)的共轭转置。
设H-1(f)为多轴试验系统的传递函数矩阵的逆矩阵,根据图2,可以得出初始驱动信号的频域序列,
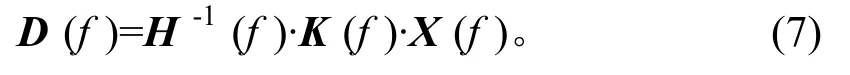
1.3 控制算法
在多轴随机振动试验过程中,由于试验系统噪声、非线性等因素的影响,使得控制系统无法非常准确地估计系统的频响函数矩阵,从而使获取的系统响应频谱矩阵与参考谱矩阵之间存在偏差。因此,在试验过程中需要对驱动信号进行实时的修正,以确保响应谱矩阵在容差范围内。
试验过程中驱动信号的修正主要通过更新多轴随机振动控制K(f)矩阵来实现[6-10],K(f)矩阵修正流程见图3。其中:x为白噪声信号矢量;Kold为待更新的K(f)矩阵;Δ为修正的误差矩阵;H为系统真实的传递函数矩阵;为实测传递函数矩阵的逆矩阵;c为系统的响应矢量。
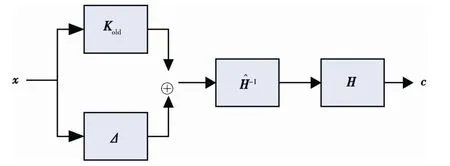
图3 多轴随机控制K 矩阵修正图 Fig.3 The correction of matrix K in the multi-axis random vibration control
在K(f)矩阵修正之前,有

响应谱密度矩阵为
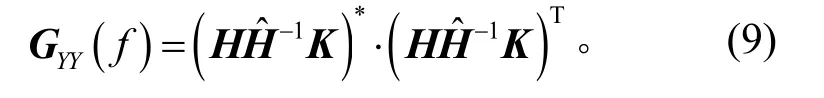
经过修正之后,响应互谱密度矩阵应该等于理想的参考谱密度矩阵GRR(f),即

联立式(9)、式(10)并展开,得
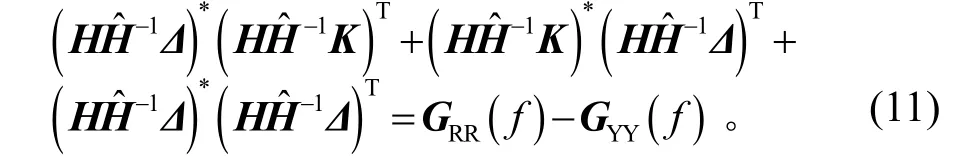
由于系统噪声及非线性等影响,系统的频响函数估计与真实的频响函数有偏差,即

式中:Ⅰ为单位矩阵;E为小误差矩阵。因而有
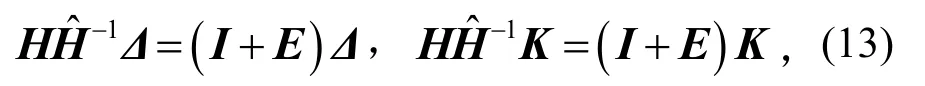
忽略EΔ,EK两矩阵小量,则式(13)可分别简化为


为确保多轴随机控制收敛,每一次闭环只能将误差的一部分用来修正,即需引入一收敛因子ε。因此控制修正算法的最终表达式为

根据公式(16)求解误差矩阵Δ后,系统的K(f)矩阵可通过式(17)进行修正和更新,
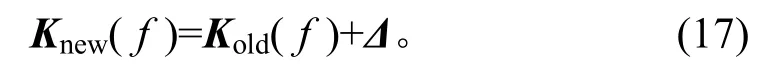
多轴随机振动控制算法流程见图4。

图4 多轴随机振动控制算法流程 Fig.4 The flow chart of the multi-axis random vibration control algorithm
2 控制系统及控制试验验证
2.1 振动台系统
三轴振动试验系统由3 个振动台、液压球头、工作台面、功率放大器、风机、液压油泵以及多轴振动控制系统等组成。三轴振动试验台见图5。单个振动台的额定推力为6 kN,球头的最大横向位移为40 mm,相对角位移为±6°,工作频率为5~2000 Hz。

图5 三轴振动试验系统 Fig.5 The triaxial vibration test system
2.2 控制系统架构介绍
多轴随机振动控制系统设计采用面向对象及功能模块分层管理的设计思想,使系统具有易用性、通用性、可维护性、可扩充性、可移植性等特点。整个系统遵循软件和硬件相对独立的设计原则,以确保通用性及可扩展性。系统的架构设计主要分成6 个层次,如图6所示。

图6 多轴随机振动控制系统层次架构 Fig.6 The framework of the multi-axis random vibration controller
2.3 试验参考条件
试验条件见表1。
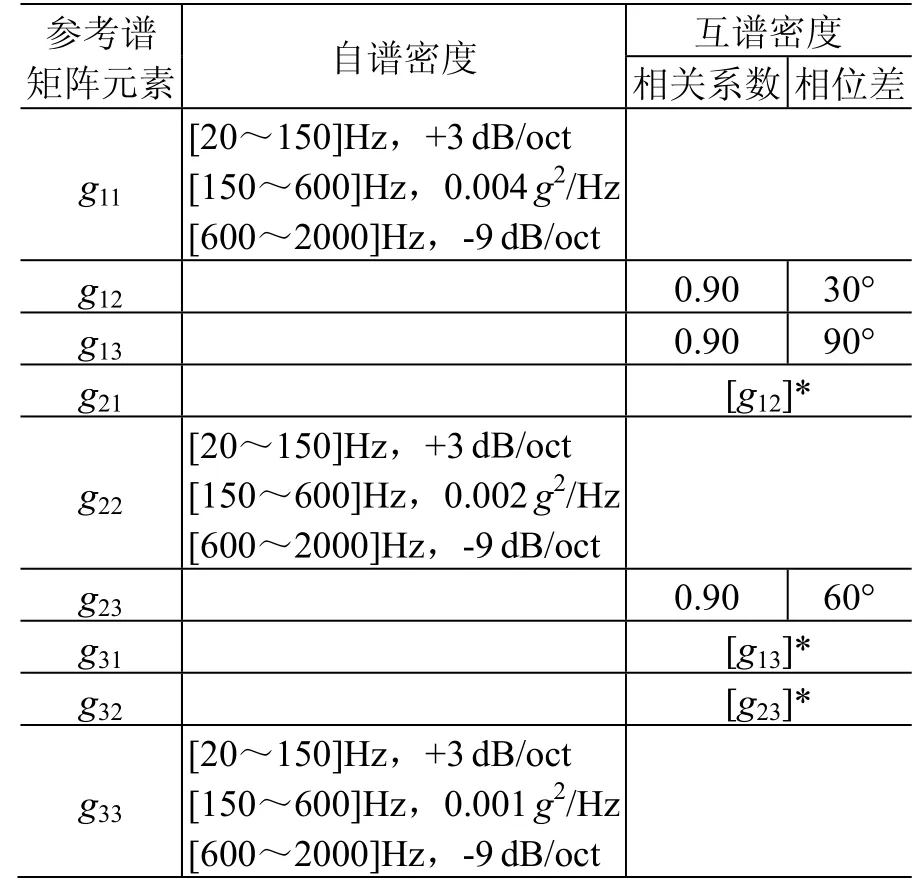
表1 三轴振动试验参考条件 Table1 The reference conditions for the tri-axial vibration test
2.4 试验结果及分析
验证试验的3 个控制点布置在工作台面上各轴向的最远端,且与各轴向保持一致(如图5所示)。为验证控制算法的可行性,按表1中的试验条件进行了一组三向随机振动试验。图7为三轴向x,y,z自功率谱密度控制曲线。图8~图10分别给出了xy,yz和xz之间的相关系数和相位差控制曲线。
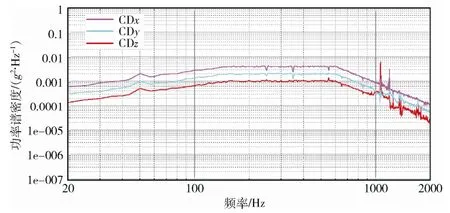
图7 三轴向x,y,z 自功率谱密度控制曲线 Fig.7 The control curve of auto-power spectral density in x,y,z directions

图8 x,y 两轴相关系数及相位差控制曲线 Fig.8 The control curve of correlation coefficient and phase difference between axes x and y
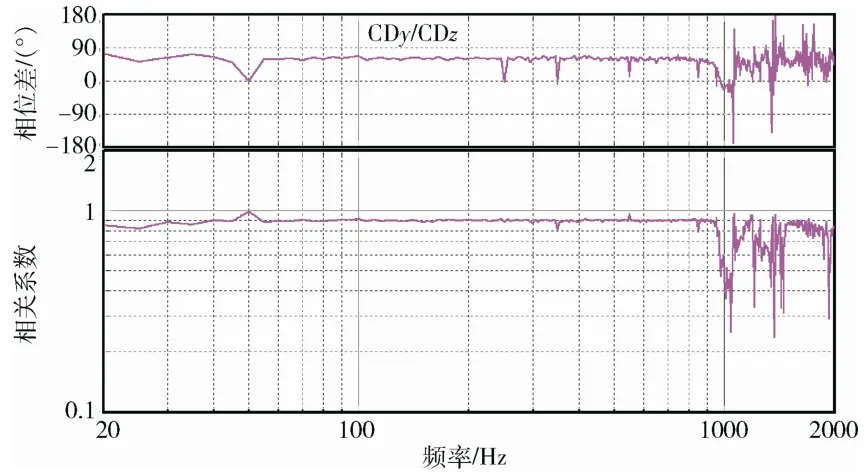
图9 y,z 两轴相关系数及相位差控制曲线 Fig.9 The control curve of correlation coefficient and phase difference between axes y and z
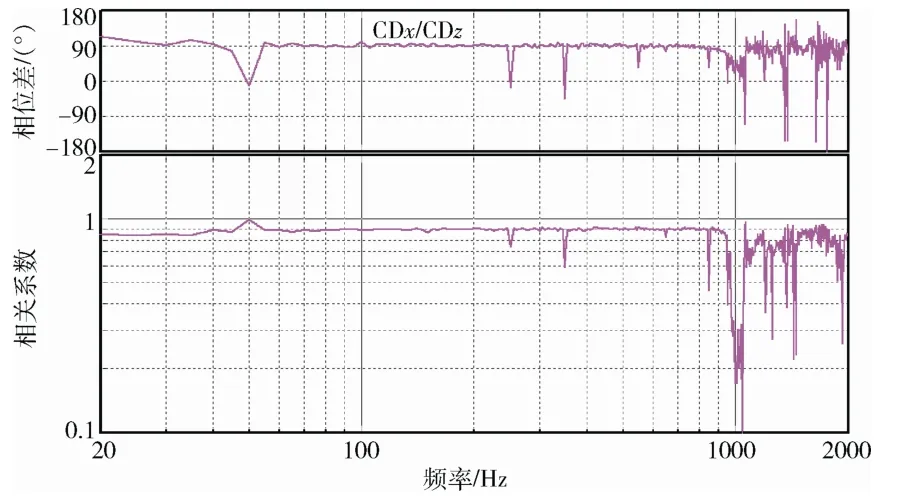
图10 x,z 两轴相关系数及相位差控制曲线 Fig.10 The control curve of correlation coefficient and phase difference between axes x and z
在多轴随机振动试验中,参考谱矩阵中互谱元素设置必须考虑轴与轴之间的物理可实现性问题[11]。此次试验,x轴与y轴之间相位差为30°,y轴与z轴之间为60°,则x轴与z轴之间必须设置为90°。同时三轴之间的相关系数均设置为0.9。
研发的多轴随机振动控制系统的动态范围优于80 dB。本次验证试验的频率范围为20~2000 Hz,谱线数为400,频率分辨率5 Hz,统计自由度为120,当试验条件到达0 dB 后,3 个控制点的自谱密度进入容差范围且保持基本稳定所需的时间约为1.0 s。多轴振动试验的容差控制准则基于中国航天科技集团标准Q/QJA108—2013《多维振动试验方法》中8.2.2 节的容差要求[12]。从此次试验自谱控制曲线可以看出,控制结果除在50 Hz 和高频若干频点略有超差外,在其他试验频率范围内的控制精度满足不超过±3 dB 要求,且超过允差的累积带宽小于整个试验频率范围的5%。50 Hz 频率处超差是由三轴试验系统的50 Hz 工频干扰引起的,可通过在功放前端引入隔离器的方法进行屏蔽解决;而1000 Hz以上高频若干频率点超差是由于球头和工作台面之间耦合特性产生的,试验前可通过调整球头相对工作台面的位置来缩小控制超差的频带,而完全解 决超差问题有一定的难度。
由于多轴振动试验的复杂性,Q/QJA108—2013 标准中对控制点之间的相干系数和相位没做规定。从此次试验控制点之间的相干系数和相位差控制曲线可以看出,在50 Hz 谐波频率处和高频处略有偏离参考条件外,在其他频带内控制效果较好,其控制精度与美国SD 公司的多轴控制系统的控制精度基本相当。总体而言,三轴随机控制效果比较理想,多轴随机控制算法的可行性得到了验证。研发的多轴随机控制系统配合三轴振动台具备为航天器小型单机产品开展多轴随机振动试验的能力。
3 结束语
本文介绍了多轴随机振动试验控制的基本理论,并应用该理论研发了一套多轴随机振动试验控制系统。利用该系统在三轴振动台上进行了一组多轴随机振动验证试验,结果表明本控制算法是可行的,控制效果较好。
研发的多轴随机控制系统只能控制三轴三自由度振动台,而在控制三轴六自由度方面,还需引入输入输出坐标转换矩阵,将传感器的线性运动转换为平动和转动等自由度后再进行控制,因此该多轴随机控制系统的控制功能还有待进一步完善。随着多轴控制技术的不断发展,它将在今后力学环境试验领域发挥越来越广泛的作用。
(References)
[1] 樊世超,冯咬齐.多维动力学环境模拟试验技术研究[J].航天器环境工程,2006,23(1): 23-28 Fan Shichao,Feng Yaoqi.Study on multi-DOF dynamic environment simulation technology[J].Spacecraft Environment Engineering,2006,23(1): 23-28
[2] Himelblau H,Hine M J.Effects of triaxial and uniaxial random excitation on the vibration response and fatigue damage of typical spacecraft hardware[C]∥Proceedings of the 66thShock and Vibration Symposium,SAVIAC.California,1995: 15-32
[3] Keller T,Underwood M A.An application of MIMO techniques to satellite testing[C]∥Proceedings: Institute of Environmental Sciences and Technology,2001: 327-339
[4] MIL-STD-810G Department of defense test method standard: Environmental engineering considerations and laboratory test: method 527,multi-exciter tests[S],2008- 10-31
[5] 祝济之,杨志鹏.多维随机振动试验中的互谱控制技术[J].航天器环境工程,2010,27(5): 621-624 Zhu Jizhi,Yang Zhipeng.Cross-spectral control technique in multi-dimensional random vibration test[J].Spacecraft Environment Engineering,2010,27(5): 621-624
[6] Smallwood D O.Random vibration testing of a single test item with a multiple input control system[C]// Proceedings of Institute of Environmental Sciences.Dallas,USA,1982: 42-49
[7] Smallwood D O.Multiple shaker random control with cross coupling[C]//Proceedings of the IES,1978: 341-347
[8] Smallwood D O.Minimum drive requirements for a multiple input multiple output linear system[C]∥Proceedings: Institute of Environmental Sciences and Technology,1986: 295-301
[9] Peeters B,Debille J.MIMO random vibration qualification testing: algorithm and practical experiments[C]//Proceedings of ESTECH 2002.Anaheim,CA,2002: 1-12
[10] Underwood M A.Multi-exciter testing applications: theory and practice[C] ∥Proceedings: Institute of Environmental Sciences and Technology.Anaheim,CA,2002: 1-10
[11] Underwood M A,Keller T.Understanding and using the spectral density matrix[C]∥Proceedings of the 76thShock &Vibration Symposium.Destin,FL,2005: 1-16
[12] Q/QJA108—2013 多维振动试验方法[S].中国航天科技集团公司,2013

