基于磁通感应的动目标探测原理及分析

黄 魁，易 忠,2，王 斌

（1.北京卫星环境工程研究所，北京 100094； 2.北京卫星环境工程研究所 可靠性与环境工程技术重点实验室，北京 100094）

0 引言

随着小型机器人、无人机、水下无人航行器等的发展和应用，人们开始高度关注对这些运动目标的磁性探测研究。其中，基于磁通感应原理的探测技术是对运动目标进行磁性探测的重要方法之一。目前，该方法已在某些领域取得广泛应用，如汽车的监测等[1]。对于复杂的运动目标（如无人航行器）的磁性探测，仅有对磁通感应探测技术进行定性研究的基础是不够的，还需要定量研究的分析参考，以提高探测精度。

为了获得探测感应线圈的响应参数与运动目标参数之间的定量关系，本文首先建立运动目标的磁偶极子模型[2]，然后在该模型的基础上推导探测线圈的磁通量及感生电动势的表达式，最后分析讨论运动目标参数及线圈结构参数对感生电动势的影响。

1 基于磁通感应的探测原理与分析

1.1 基本原理

磁通感应探测的基本原理是基于法拉第电磁 感应定律：对于一个尺寸确定的静止闭合线圈，当一个磁性运动目标穿过其中时，会引起磁通量的变化，进而产生感生电动势；感生电动势与回路交联的磁通量变化率的负值成线性关系，即V= -N·dΦ/dt。通过对感生电动势的定量计算以及分析，可以反演出该运动目标的某些磁特性参数。

当运动目标与探测线圈间的距离较小时，其磁场可以用多偶极子进行模拟；距离较大（大于目标尺寸的5～6 倍）时，则可以把其看作一个磁偶极子[3-6]，如图1所示。本文要讨论的是远距离情况，故可以将运动目标的磁场简化为一个磁偶极子模型，下面是在该模型的基础上开展探测信号对运动目标特征的响应关系研究。

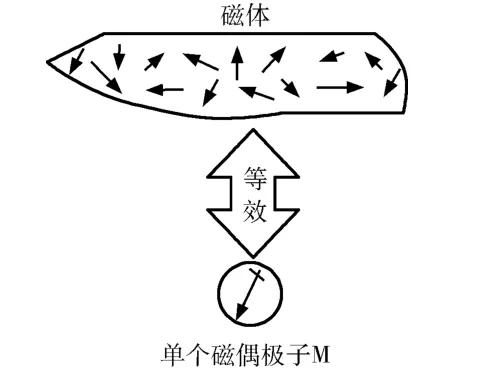
图1 运动目标磁性的磁偶极子等效模型 Fig.1 Magnetic dipole model for the magnet field of moving target

1.2 磁偶极子在空间某一点处的磁感应强度推导

为了对磁性运动目标对探测闭合线圈内感生电动势的变化进行定量分析，需要推导磁偶极子在空间某一点处的磁感应强度。设磁偶极子的磁矩大小为M，为便于推导分析，又将磁偶极子简化为一个圆电流[7]，并建立磁偶极子及其坐标系，如图2所示。坐标系原点O位于磁偶极子的中心，z轴正向指向磁矩矢量的方向，x轴与y轴指向符合右手定则。E为空间某一点，其球坐标为E(r,φ0,θ0)。

图2 磁偶极子及坐标系 Fig.2 The coordinate system of the magnetic dipole

设圆电流的强度为Ⅰ，圆的半径为R，r为圆心O到空间E点的距离。磁偶极子的磁矩大小m为

其中：S为圆电流所围的面积，即S=π·R2；n为圆电流的平面正法向量，其方向与电流方向符合右手规则。

设磁偶极子所在空间充满磁导率为µ的介质，在圆周上任一点F(R,/2π ,θ)处截取电流元Ⅰdl，根据毕奥-萨伐尔定律[8]，该电流元在空间点E处所产生的磁感应强度矢量为

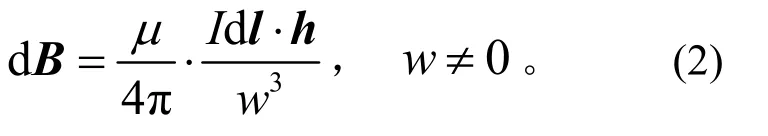
其中dl为F点处的圆周切向量，h为向量FE，w为FE 的模，

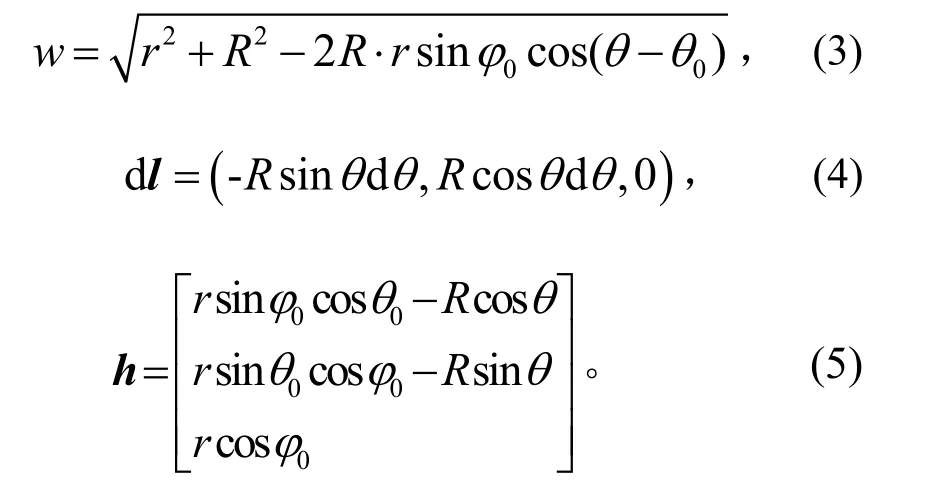
设磁感应强度向量为B=Bxi+Byj+Bzk，将 式(3)～式(5)代入式(2)，再由级数知识推导整理并根据磁矩概念得到[9]

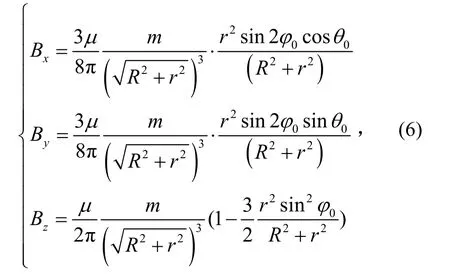
该式就是空间点E(r,φ0,θ0)的磁感应强度三分量表达式。

对于远场，即Rr＜＜ 的情况，可以将R省略掉并简化，故只要得到磁偶极子的磁矩，空间某一点的磁感应强度向量均可用式(6)求得。

1.3 某一时刻矩形线圈内磁通量推导

假设在地面铺设了一个矩形探测线圈，其长度为a，宽度为b，匝数为N。取矩形中心为原点，直角坐标系如图3。图中的Q(xq,0,zq)点为运动目标（其磁场等效为一个磁偶极子），其磁矩大小为m。Q点在线圈正上方沿x轴正方向以速度v匀速通过。在矩形线圈内任取一点P，其坐标为(xP,yP,0)。

图3 线圈系统坐标系 Fig.3 The coordinate system of the coil system

由于本文探讨的是远距离情况，即R＜＜r，可视R≈0 处理，故磁偶极子Q在P点处的磁感应强度可由公式(6)求得。由磁通量表达式Φ=BS，故dΦ=B· dS=B· dx· dy，通过对线圈所围平面积分即可以得到矩形内部的磁通量大小。

由于穿过矩形线圈的磁通量大小仅与垂直于矩形线圈所在平面的磁感应强度有关，根据磁偶极子磁矩方向的不同可分成3 种情况讨论。

1）磁矩方向为z轴正方向

由坐标变换可得，矩形线圈内磁通量与图2所示磁偶极子坐标系下Bz有关，其中R≈0，r=代入式(6)后整理得到

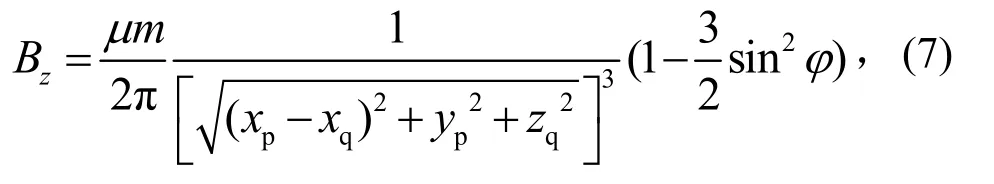
则矩形线圈的磁通量为

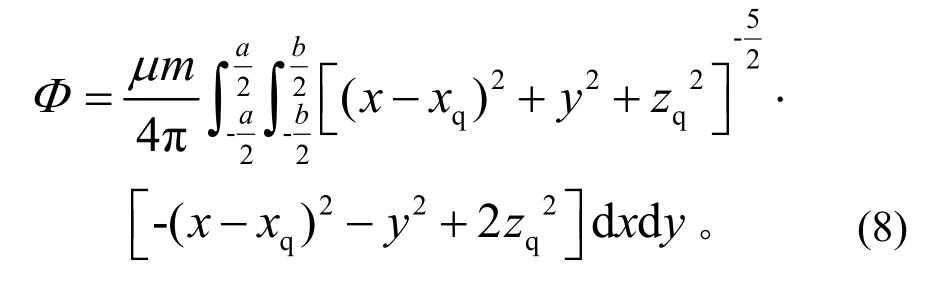
2）磁矩方向为x轴正方向

同样的道理，根据

得矩形线圈的磁通量为

3）磁矩方向为y轴正方向

根据

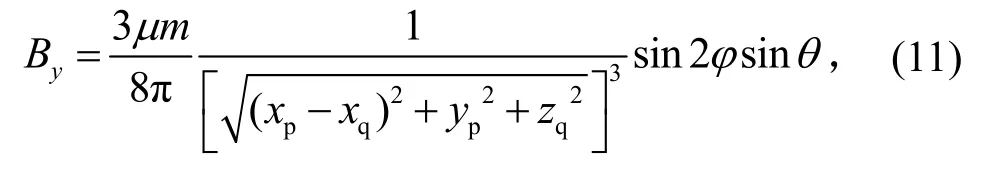
则矩形线圈的磁通量为

1.4 某一时刻线圈内的感生电动势推导

根据法拉第电磁感应定律，把磁通量对时间t微分可得该时刻的感生电动势U，由于公式较为复杂，无法得到解析解，故采用数值方法计算。

2 仿真计算

运动目标的磁矩取m=50 А·m2；目标沿x轴运动的速度v=1 m/s，等效磁偶极子距线圈的高度zq=20 m，初始位置xq为-100 m，运动时间为200 s；线圈长度a=20 m，宽度b=5 m，匝数N=100；线圈缠绕方向选定后，则磁导率取为µ=4π×10-7H/m。根据上述参数，采用数值方法计算，利用软件作图 得到磁通量和感生电动势的变化规律。

根据磁偶极子磁矩方向的不同分2 种情况讨论。

1）磁矩方向为x轴正方向

根据式(10)进行仿真计算，磁通量和感生电动势的计算结果如图4和图5所示。

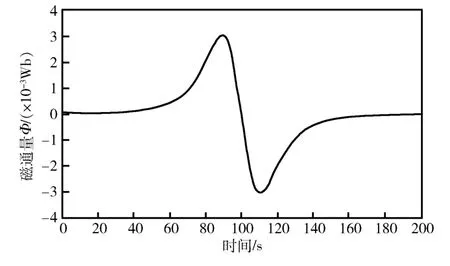
图4 磁通量变化规律（x 轴） Fig.4 The variation of magnetic flux (x axis)

图5 感生电动势变化规律（x 轴） Fig.5 The variation of induced electromotive force (x axis)

从图4、图5可知，当磁偶极子在线圈上方匀速通过矩形线圈时，矩形线圈内产生的磁通量从0开始逐渐增大至极值后迅速减小，到达线圈中心处时为0，继续向负方向变化至负极值，之后逐渐增大至0。其感生电动势随时间由0 开始逐渐反方向增大至负极值，之后沿正方向不断快速变化，到达线圈中心时达到正的极大值，之后快速变化至同一负极值，最后由负极值逐渐衰减到0。

2）磁矩方向为z轴正方向

根据式(8)进行仿真计算，磁通量和感生电动势的变化规律分别如图6与图7所示。

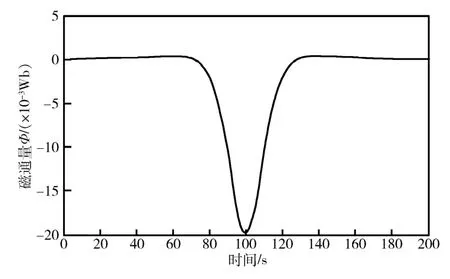
图6 磁通量变化规律（z 轴） Fig.6 The variation of magnetic flux (z axis)

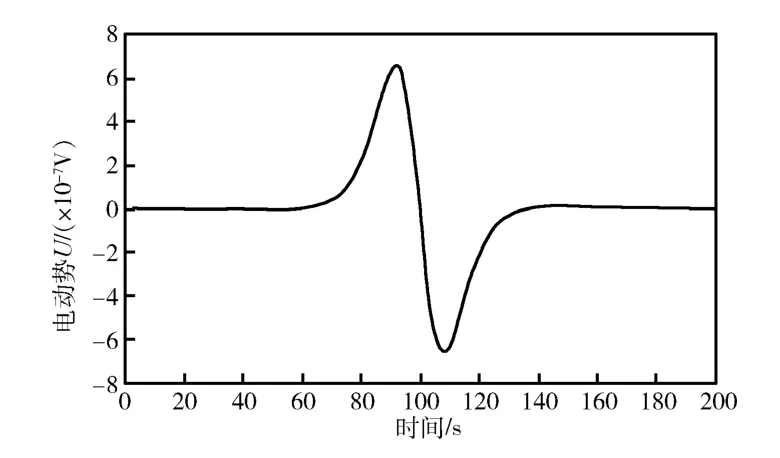
图7 感生电动势变化规律（z 轴） Fig.7 The variation of induced electromotive force (z axis)

图6、图7中所示变化规律与理论分析及实验结果一致。

对于磁矩任意指向的磁偶极子，计算其感生电动势时，将其磁矩沿x轴,y轴,z轴分解，分别进行计算，再将各自产生的感应电动势叠加即可。

3 运动目标参数对感生电动势的影响分析

由理论分析和仿真计算结果可以得到，运动的磁偶极子会引起探测矩形线圈的感生电动势变化。以磁偶极子的磁矩方向为x轴正方向为例，来讨论分析运动目标对感生电动势的影响。

1）高度zq对感生电动势的影响

高度zq分别取20、25、30、35 m，其他参数选取与第2 章相同。计算结果如图8所示。

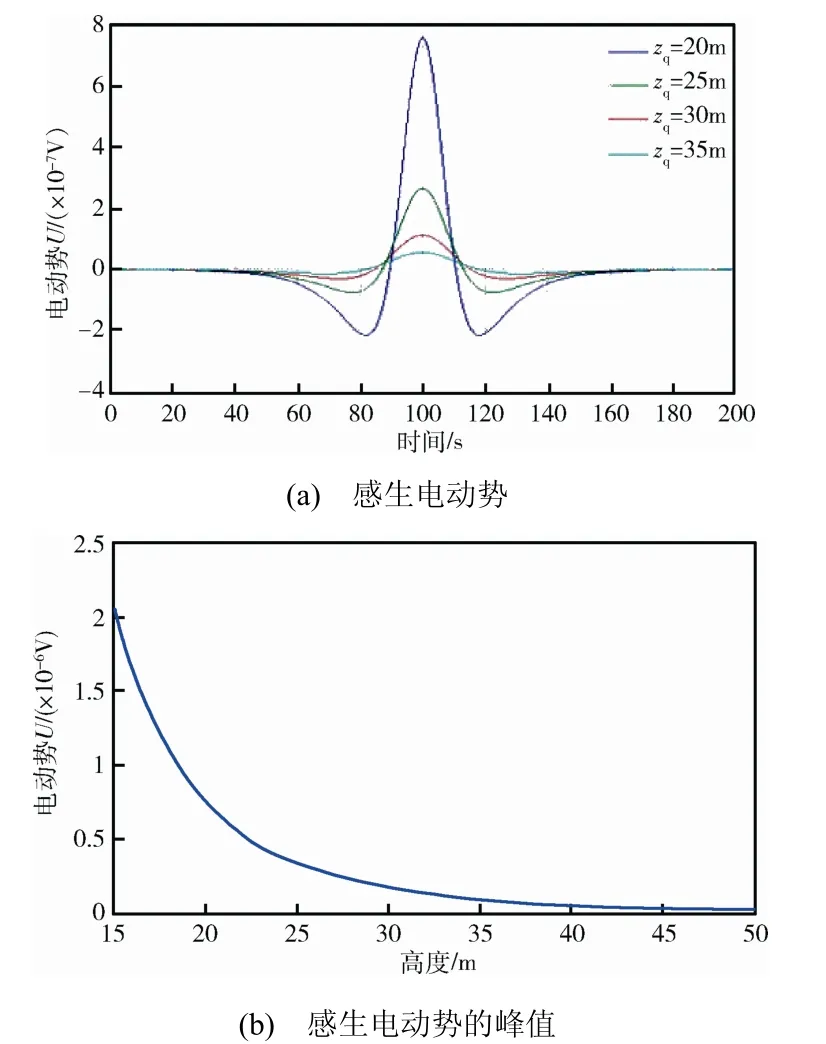
图8 运动目标高度对感生电动势的影响 Fig.8 The influence of height zq on induced electromotive force

由图8可以看出，随着zq的增加，感生电动势峰值呈减小趋势，峰值与zq成负指数关系。

2）运动速度对感生电动势的影响

速度v分别取2.0、1.5、1.0、0.5、0.25 m/s，其他参数不变。计算结果图9所示。

从图9中可以看出，随着速度v的增加，感生电动势峰值成线性增大。

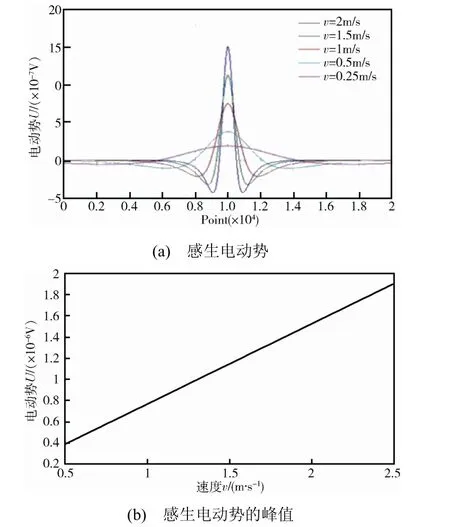
图9 运动目标速度对感生电动势的影响 Fig.9 The influence of velocity on induced electromotive force

4 线圈尺寸参数对感生电动势的影响分析

由理论分析可知，当线圈尺寸与zq为同一量级时，尺寸越大，则感生电动势越大。由于影响关系较为复杂，本文仅取2 种情况作简单分析。线圈尺寸分别取(a=20 m,b=5 m)和(a=20 m,b=30 m)，其他参数选取与第2 章相同。计算结果如图10所示。

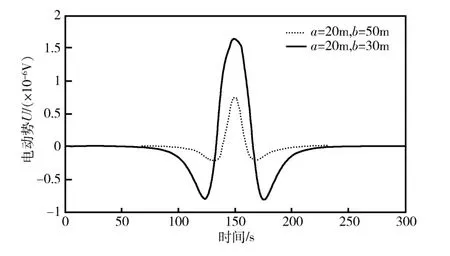
图10 线圈尺寸对感生电动势的影响 Fig.10 The influence of coil size on induced electromotive force

从图10中可以看出，在一定范围内，当线圈尺寸增加时，则感生电动势会有一定程度的增大。

5 结论

本文针对磁性运动目标对矩形探测线圈的磁通量和感生电动势的影响开展了理论分析和仿真计算，得到下列结论：

1）感生电动势峰值随运动目标至线圈距离的增加成指数关系增加；

2）感生电动势峰值随目标运动速度的加快成线性关系增大；

3）在一定范围内，感生电动势峰值随线圈尺寸的增加而增大。

通过定量分析，初步验证了基于磁通感应原理的探测技术对运动目标磁性探测的可行性。随着运动目标和空间环境变化的复杂多样，如何根据探测信号反演出运动目标特性参数，以及如何优化线圈结构设计，有必要开展更深入的研究。

（References）

[1] 臧利林,贾磊,秦伟刚,等.基于环形线圈车辆检测系统的研究与设计[J].仪器仪表学报,2004,25(4): 329-331 Zang Lilin,Jia Lei,Qin Weigang,et al.Research and design of detecting car system based on loop-coil in traffic[J].Chinese Journal of Scientific Instrument,2004,25(4): 329-331

[2] 张朝阳,肖昌汉,高俊吉,等.磁性物体磁偶极子模型适用性的试验研究[J].应用基础与工程科学学报,2010,18(5): 862-868 Zhang Chaoyang,Xiao Changhan,Gao Junji,et al.Experiment research of magnetic dipole model applicability for a magnetic object[J].Journal of Basic Science and Engineering,2010,18(5): 862-868

[3] 唐劲飞,龚沈光,王金根.基于磁偶极子模型的目标定位和参数估计[J].电子学报,2002,30(4): 614-616 Tang Jinfei,Gong Shenguang,Wang Jin’gen.Target positioning and parameter estimation based on magnetic dipole model[J].Acta Electronica Sinica,2002,30(4): 614-616

[4] Salem A,Ushijima K.Automatic detection of UXO from airborne magnetic data using a neural network[J].Subsurface Sensing Technologies and Applications,2001,2(3): 191-213

[5] Takayuki Inaba,Akihiro Shima,Masaharu Konishi.Magnetic dipole signal detection and location using subspace method[J].Electronics and Communications in Japan,2002,85(5): 23-34

[6] 齐燕文.空间磁环境模拟技术[J].航天器环境工程,2005,22(1): 19-21 Qi Yanwen.Space magnetic environment simulation technology[J].Spacecraft Environment Engineering,2005,22(1): 19-21

[7] 何亚军,桂良启.电磁场与电磁波[M].北京: 清华大学出版社,2013: 162-164

[8] 蒋学华.计算磁偶极子磁场的一种方法[J].泉州师范学院学报: 自然科学,2002,20(4): 89-91 Jiang Xuehua.A method of magnetic field with magnetic dipoles[J].Journal of Quanzhou Normal College: Natural Science,2002,20(4): 89-91

[9] 任来平,赵俊生,侯世喜.磁偶极子磁场空间分布模式[J].海洋测绘,2002,22(2): 18-21 Ren Laiping,Zhao Junsheng,Hou Shixi.The magnetic field space distribution pattern of magnetic dipoles[J].Hydrographic Surveying and Charting,2002,22(2): 18-21