徜徉建筑之林,欣赏艺术之美
——八年级上册第三单元综合性学习创新设计
□徐飞
□李庆社
徜徉建筑之林,欣赏艺术之美
——八年级上册第三单元综合性学习创新设计
□徐飞
中国古代建筑如一幅巨大的立体画,展现了中华民族灿烂与辉煌的历史;如一首凝固的音乐,演奏着中华民族智慧与奇迹的乐章。让我们走近中国古代建筑,去探寻美、领略美、升华美吧!
一、注重积累,了解建筑之悠久
1.中国古建筑,既注重质量,又讲求美观,还追求特色,也因此形成了中国古代建筑实用性与艺术性相融合的特点。反映在文字上,便产生了一批含义丰富、富有想象力的成语。请写出描写建筑的成语,不少于四个。
________ ________
________ ________
2.建筑是人的杰作,是劳动人民智慧与汗水的结晶。在中国建筑行业史中,出现了无数能工巧匠,请写出中国历史上在建筑行业较有影响的人物,不少于三个。
________ ________ ________
3.褪尽历史的繁华,远离尘世的喧嚣,有一批古代建筑,或殿宇,或亭台,或园林,至今屹立在华夏大地上,成为历史永恒的见证,也成为当地永远的名片。请按要求写出这些代表建筑:
(1)东方三大殿:________、________、________
(2)江南三大名楼:________、________、________
(3)中国四大名亭:、________ ________、________、________
二、用心识别,欣赏建筑之精美
1.下面四张图片是代表中国古建筑的典范之作,也是其所在城市地标性建筑,请依次写出其建筑名称和所在地。

(1)________(2)________
(3)________(4)________
2.古往今来,文人墨客们大都喜欢游历天下,他们攀名山、赴大川、登高楼、赏园林……所到之处,各具特色的建筑也激发了他们内心蕴含的情感,催生出许多名篇佳作,从而,很多建筑也因他们留下的文字而更加具有文化内涵与人文价值。赏析下列诗句,请准确说出这些诗文名句分别是描写哪个著名建筑的。
A.欲穷千里目,更上一层楼。
B.落霞与孤鹜齐飞,秋水共长天一色。
C.十里青山行画里,双飞百鸟似江南。
D.晴川历历汉阳树,芳草萋萋鹦鹉洲。
E.河桥残月晓苍苍,照见卢沟野水黄。
A.________B.________C.________
D.________E.________
三、仔细品味,明确建筑之特色
从最开始的穴居、巢居,到土木结构房屋,再到独立完整的建筑体系,总体而言,中国古代建筑主要有礼仪典礼型、贵族宫室型、居民住宅型、观赏园林型。下列文字分别是这四种类型建筑的介绍文字,读后请简要归纳其特点。
1.(北京天坛祈年殿)祈年殿呈圆形,座落于高6米的三层汉白玉圆形栏杆之上,直径32米,高38米,是一座有鎏金宝顶的三重檐的圆形大殿,殿檐颜色深蓝,是用蓝色琉璃瓦铺砌的,因为天空是蓝色的,以此来象征天空。进入祈年殿内,可以看到天花板雕饰了彩绘的“九龙藻井”,有雕刻得神态生动活泼的“龙凤呈祥”的图案,行云流水般的精细雕饰令人不禁赞叹古代工匠技艺的妙绝。
2.(故宫博物院)太和殿俗称金銮殿,高28米,面积2380多平方米,是故宫最大的殿堂。在湛蓝的天空下,那金黄色的琉璃瓦重檐屋顶,显得格外辉煌。殿檐斗拱、额枋、梁柱,装饰着青蓝点金和贴金彩画。正面是12根红色大圆柱,金琐窗,朱漆门,同台基相互衬映,色彩鲜明,雄伟壮丽。
3.(江南水乡乌镇)乌镇的建筑群距今已有2000多年沧桑的历史,但现在仍完整地保存着原有水乡古镇的风貌和格局。乌镇所有的房屋,都是临水而居、面水而居、跨水而居。全镇以河成街,桥街相连,依河建屋,黑瓦白墙,河道廊坊,临河水阁,古色古香,水镇一体,呈现出一派恬静、优雅的清静,是江南典型的“小桥、流水、人家”。
4.(苏州园林)至于池沼,大多引用活水,有些园林池沼宽敞,就把池沼作为全园的中心,其他景物配合着布置。水面假如成河道的模样,往往安排桥梁。如果要安排两座以上的桥梁,那就一座一个样,绝不雷同。池沼或河道的边沿很少砌齐整的石岸,总是高低屈曲随其自然。
1.________________
2.________________
3.________________
4.________________
四、潜心领悟,形成建筑之思想
梁思成是中国现代杰出的建筑学家。他与妻子林徽因一起,奔走各地,为祖国的古建筑建档,倾注了所有的心血。1949年,新中国成立后,针对北京城内的古建筑,梁思成提出了很好的保护与城市建设意见,却因为城市发展的需要而未被采纳,于是,北京城内,大批精美的牌楼、巍峨的城楼被拆除了。
几十年过去了,如果梁思成的建议被采纳,北京会留下许多令人骄傲的古建筑。
1.读了上面这个故事,你对保护古建筑有什么看法和认识?
2.古建筑是一个国家、民族的瑰宝,请你拟一条宣传标语,号召人们保护古建筑。
参考答案:
一、1.飞阁流丹桂殿兰宫雕梁画栋雕栏玉砌2.墨翟鲁班李春3.(1)北京紫禁城的太和殿、曲阜孔庙的大成殿、泰山岱庙的天贶殿;(2)岳阳楼(湖南岳阳)、滕王阁(江西南昌)、黄鹤楼(湖北武汉);(3)安徽滁州的醉翁亭、北京的陶然亭、湖南长沙的爱晚亭和杭州西湖的湖心亭。
二、1.(1)北京市,天坛;(2)陕西西安,大雁塔;(3)四川乐山,乐山大佛;(4)西藏拉萨,布达拉宫。2. A.鹳雀楼;B.滕王阁;C.颐和园;D.黄鹤楼;E.卢沟桥。
三、1.高大恢弘,雕刻精细,庄重严肃;2.气势雄伟,装饰华丽,金碧辉煌;3.水乡古镇,造型简朴,有地域特色;4.建筑与山水结合,布置和谐,自由委婉,讲求自然之美。
四、1.示例:我认为,应当保护古建筑。古建筑是一个国家历史的见证,是一民族文明的象征。它的存在,让一个城市,有着浓厚的文化气氛,让一个国家有着骄傲的历史底蕴。毕竟,古建筑如果被毁灭能恢复的只是其形,而失去其文化与历史的真实,那将是一个国家和民族的精神损失。2.示例:保护古代建筑,留下历史足迹。
解读乘法公式
□李庆社

一、平方差公式
两个数的和与这两个数的差相乘,它们的积就等于这两个数的平方差,即(a+b)(a-b)=a2-b2.
平方差公式是特殊的多项式乘法,要理解并掌握公式的结构特征.
(1)必须是两个二项式相乘;
(2)必须有一项完全相同,另一项互为相反数;
(3)结果是相同项的平方减去互为相反数的项的平方.
公式中的a与b可以是数,也可以换成一个代数式.
平方差公式的几何解释
如图1,阴影部分的面积可以看成是大正方形的面积减去小正方形的面积,即a2-b2;若把小长方形Ⅲ旋转到小长方形Ⅴ的位置,则此时的阴影部分的面积又可以看成SⅠ+SⅣ+SⅢ=SⅠ+SⅣ+SⅤ=(a+b)(a-b).从而验证了平方差公式(a+b)(ab)=a2-b2.

图1
例1计算(m+n)(m-n)+3n2.
解析:(m+n)(m-n)+3n2
=(m2-n2)+3n2
=m2+2n2.
点评:在混合运算中,用平方差公式直接计算所得的结果可以写
在一个括号里,以免发生符号错误.
例2已知:符合前面式子的规律,则
a+b=_________.
解析:通过观察分析知道,…,由此可知分母上的数是分子上的数的平方减1,而是题给序列中的第9项,则b=10,a=102-1=99,所以a+b=109.
点评:等式左右两边的数字特征是:整数部分是完全平方的关系,而分数是相同的,且每一个分数的分母又等于分子上的数与1的平方差.
二、完全平方公式
两数和(差)的平方,等于它们的平方和加上(减去)它们乘积的2倍,即(a±b)2=a2±2ab+b2.
(1)完全平方和公式的特点:左边是两个数的和(或差)的平方,右边是这两个数的平方和,再加上(或减去)这两个数积的2倍.
(2)公式中的字母a、b可以表示具体的数(正数或负数),也可以表示单项式或多项式等式子.
例3多项式9x2+1加上一个单项式后,使它能成为一个整式的完全平方公式,那么加上的单项式可以是_________(填上一个你认为正确的即可).
解析:由完全平方公式的结构特点可知,要使多项式9x2+1加上一个单项式后,能成为一个整式的完全平方公式,则可以填上单项式:-1,或-9x2,或6x,或-6x,或,等等.
点评:要使原多项式9x2+1加上一个单项式后能成为一个整式的完全平方公式,这个整式可以是单项式,也可以是多项式,于是本题的答案不惟一,只要符合题意即可.
例4计算:9982.
解析:此题直接运算比较麻烦,仔细观察发现998=1000-2,于是可化为完全平方公式的形式求解,即9982=(1000-2)2=10002-2× 1000×2+22=996004.如果感到此法用起来有点繁琐,还有没有其他的方法呢?我们可以这样转化:9982=(9982-22)+22=(998+2)(998-2)+4=1000×996+4=996004.同样是运用公式,哪种方法更适合你?
点评:乘法公式是初中数学的重要内容,应用十分广泛.解题时,若能根据题目特点,创造性地运用乘法公式,将会给我们带来极大的方便.
完全平方公式的图形解释
如图2,大正方形的面积可以表示为(a+b)2,也可以表示为S=SⅠ+SⅡ+SⅢ+SⅣ,即S=a2+ab+ab+b2=a2+2ab+b2.从而验证了完全平方公式(a+b)2=a2+2ab+b2.
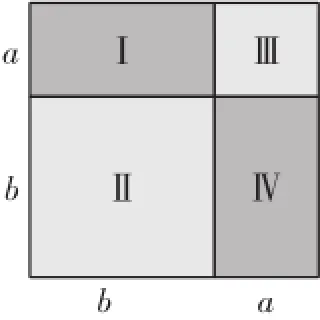
图2
例5如图3,是由四个形状大小完全相同的长方形拼成的图形,利用面积的不同表示法,写出一个代数恒等式:.

图3
解析:利用面积的割补原理,可列出(a+b)2=(a-b)2+4ab,或(a+b)2-4ab=(a-b)2,或(a+b)2-(a-b)2=4ab.
点评:如何展示一个代数恒等式的几何意义,又如何从一个图形中挖掘提炼一个抽象的代数恒等式,成为近年中考命题的一大亮点
例6在边长为a的正方形中挖去一个边长为b的小正方形(a>b),再沿虚线剪开,如图4(1),然后拼成一个梯形,如图4(2),根据这两个图形的面积关系,表明下列式子成立的是()a2-b2,图(2)的面积为(2a+2b)(a-b)=(a+b)(a-b).故选A.

图4
A.a2-b2=(a+b)(a-b)
B.(a+b)2=a2+2ab+b2.
C.(a-b)2=a2-2ab+b2
D.a2-b2=(a-b)2
解析:图(2)是由图(1)中的两部分拼凑而成,故两者的面积相等,用面积公式可以判断所给的选项中,哪个是正确的.
图(1)中阴影部分的面积为a2-b2,图(2)的面积为(2a+2b)(a-b)=(a+b)(a-b).故选A.
点评:本题的关键之处在于抓住两个图形中阴影部分的面积相等,从而可确定哪个选项是正确的.它可用作验证乘法公式的正确性.

