光学作图法在测量设计中的应用

□徐俊兵

光学作图法在测量设计中的应用

□徐俊兵

光学作图很多都属于几何作图，而且通过作图构建出了一些几何图形和几何数量关系，利用这些数量关系其实也可以帮助我们完成某些间接测量.下面举例说明光学作图法在测量设计中的广泛应用.

应用一：测高度

例1请选用必需的器材估测旗杆的高度.画出你所用测量方法的示意图，并列出旗杆高度的表达式.

可供选择的器材：竹竿一根、平面镜一块、利用小孔成像原理制成的照相机（即针孔照相机）一架、卷尺一把、课桌一张、木制直角三角尺一把.

解析：此题综合考查同学们运用光学知识解决实际问题的能力，具有开放性，由同学们自主选择器材，方法多样，因此正确运用光学中的有关原理、规律是确保方法得当的关键.

方法一：选用竹竿一根、卷尺一把.引用日常生活中的“影子现象”，并借助数学中相似三角形对应边成比例的知识解题.

方法二：选用平面镜一块、卷尺一把.运用光的反射定律和平面镜成像特点，借用相似三角形知识解题.

方法三：选用直角三角尺一把、卷尺一把、课桌一张.运用光的直线传播知识并借助相似三角形的知识解题.

方法四：选用针孔照相机一架、卷尺一把.利用小孔成像解题.

现就方法二具体操作如下：（其他方法留给同学们自己思考）

在距旗杆L处的地面上放一块小平面镜，人后退至能在平面镜中看到旗杆顶端时停止，测出人与平面镜的距离l和眼睛距地面的高度h，设旗杆高度为H.如图1所示，根据光的反射定律和相似三角形知识可知：

图1

应用二：测宽度

例2现有如下实验器材：标杆（竹竿）2根、卷尺一把.试用作图法测河的宽度，并列出计算河宽的表达式.

解析：应用光的直线传播原理可以测量河道的宽度.如图2所示，先用一根竹竿正对河对岸边上O点处的一棵大树（或其他物体），竖直插在河边A点上，再用另一根竹竿竖直插入B点，观察到两根竹竿与树干恰好重合在一条直线上，测得AB之间的距离为l，然后将A竿向左移动l1，B竿向左移动l2，直到使它们再次重合在一直线上.由光的直线传播原理和相似三角形知识可知：△OAA′∽△OBB′，且对应边成比例，AB=l，AA′=l1，BB′=l2，代入上式得：的宽度.

图2

应用三：确定位置

例3如图3所示，在一条公路的同侧分别有A、B两个村庄，现要在公路旁新建一个车站，使得车站到两村的距离最短.请帮忙确定车站的位置.

图3

解析：该题图与从A点发出光线经过平面镜反射后通过B点的光路图很相似.利用全等三角形和两点间的距离最短等知识，再结合平面镜成像的特点就很容易确定车站的位置.具体操作如下：找出A村以公路为“平面镜”的“像点”（即找出A村以公路为对称轴的对称点A′），连接A′B与公路的交点O就是新建车站的位置.如图4所示，由平面镜成像特点可知：△ACO≌△A′CO，所以A′O=AO.因为A′OB在同一直线上，A′B最短，即AO+BO最短.

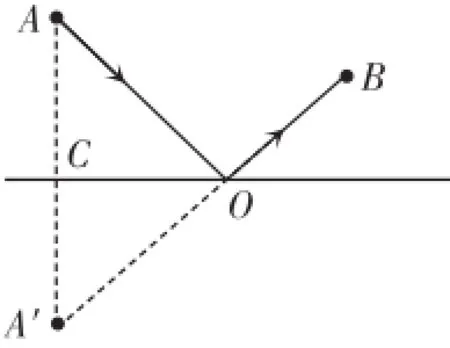
图4

应用四：寻找快捷路径

例4如图5所示，小明从家A点到达学校C点必须经过一片平地和一片沙地（平地行走速度大于沙地行走速度），他应选择怎样的路径最快捷？请你画出他行走的大致路线.

图5

解析：小明从家到学校，怎样的路径最快捷？这是运动学问题，它与光学知识有什么关联？光的哪个传播规律与它相似？这是解答本题的难点所在.

该题图与光从A点发出照到水中C点的光路图很相似.从本质上讲，光在空气中的传播速度比在水中大，当光从空气中射入水中时，光路突然发生了偏折，但它从A点到C点是最省时的.同样人在平地上行走的速度大于在沙地行走的速度，两处速度不同，这点与光从空气射入水中很相似.由于从A点射出的光照到C点，入射点在B点右侧，故小明要快捷地到达C点，进入沙地的位置也应该在B点的右侧D点处.小明的行进路线如图6所示.

图6