妙用幂的“逆运算”

□胡军

妙用幂的“逆运算”

□胡军

同学们都知道，幂的乘法运算包括同底数幂的乘法、幂的乘方、积的乘方，其运算法则的表达式分别为：am·an＝am+n，（am）n＝amn，（ab）n＝anbn（m、n为正整数）.在解题过程中，根据算式的结构特征，巧妙地逆用这几个法则，常可以化繁为简，化难为易，使很多棘手的问题迎刃而解.

一、逆用法则化简求值

例1计算：

分析：由于与正好互为倒数，其乘积为1.故先逆用同底数幂的乘法法则，将

逆用积的乘方即可.

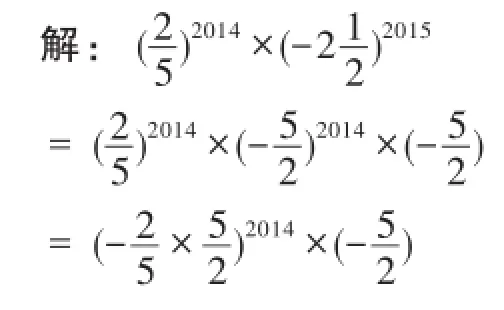
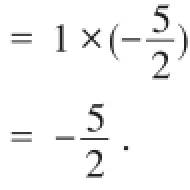
例2已知a2n＝2，求（2a3n）2－3（a2）2n的值.

分析：显然，由条件直接求出a是不可能的.我们不妨先对求值式进行幂的“正运算”，然后逆用幂的乘方法则，使之出现a2n，再整体代入即可.

解：（2a3n）2－3（a2）2n

＝4a6n－3a4n

＝4（a2n）3－3（a2n）2.

∵a2n＝2，

∴（2a3n）2－3（a2）2n

＝4×23－3×22

＝32－12

＝20.

二、逆用法则确定个位数字

例3试确定52014×72015的个位数字.

分析：本例若通过直接运算来求乘积的个位数，显然不可取，而逆用同底数幂的乘法及积的乘方法则，可使问题巧妙获解.

解：52014×72015

＝52014×72014×7

＝（5×7）2014×7

＝352014×7.

因为个位数字为5的数的任何次幂的个位数字仍是5，再与7相乘，其乘积的个位数字还是5，所以最后结果的个位数字为5.

三、逆用法则比较大小

例4试比较255、344、433的大小.

分析：这三个幂运算后的数字都非常大，直接计算相当困难，考虑到三个算式的指数都与11有关，所以可逆用幂的乘方法则，把它们化为同指数的幂，然后比较底数的大小即可.

解：（1）∵255＝（25）11，

344＝（34）11，433＝（43）11，

∵25＝32，34＝81，43＝64，

又∵32＜64＜81，

即25＜43＜34，

∴255＜433＜344.

四、逆用法则说理论证

例5试说明353－333是10的整数倍.

分析：要说明353－333是10的倍数，只要说明353－333能被10整除，即说明353－333的个位数字是0即可.由353－333的数字的特点可逆用幂的乘方法则，分别求出353和333的个位数字，再说明其差的个位数字为0.

证明：∵353＝（34）13×3

＝8113×3，

其个位上的数字为3，

333＝（34）8×3＝818×3，

其个位上的数字也是3.

∴353－333的个位上的数字是0，即353－333是10的整数倍.