分数阶Hopfield型神经网络的全局渐近稳定性

崔世维，盖明久，刘孝磊

（海军航空工程学院a.研究生管理大队；b.基础部，山东烟台264001）

分数阶Hopfield型神经网络的全局渐近稳定性

崔世维a，盖明久b，刘孝磊b

（海军航空工程学院a.研究生管理大队；b.基础部，山东烟台264001）

研究了分数阶Hopfield型神经网络的全局渐近稳定性，通过LMI方法得到了一种实现系统全局渐近稳定性的LMI形式条件，通过实例仿真验证了结论的正确性。

分数阶；神经网络；渐近稳定性；LMI

随着对分数阶微积分的认识越来越深刻，分数阶微积分在多个学科有广泛应用，如物理、化学、生物和图像处理等，并且取得了较好的研究成果，凸显了其独特的优势和不可替代性，其理论和应用研究引起了广泛重视，已经成为当前国际上的一个研究热点[1-7]。

众所周知，小到一个具体的控制系统，大至社会系统、金融系统、生态系统，总是在各种偶然的或持续的干扰下进行的，保持系统的稳定性就显得至关重要。因此，研究分数阶系统也必不可免地面临着对稳定性的研究。目前，关于分数阶系统稳定性的研究结果主要涉及分数阶系统的有限时稳定性、鲁棒稳定性、Mittag-Leffler稳定性等[8-11]。然而，由于分数阶微积分定义的不统一以及定义本身的复杂性，导致对分数阶系统稳定性的研究面临着众多困难。

另一方面，由于神经网络良好的非线性映射能力、自学习适应能力和并行信息处理能力，为解决不确定非线性系统的建模和控制提供了新思路。随着分数阶微积分的发展，人们将分数阶微积分引入到神经网络，建立了分数阶神经网络，并取得了一定的研究成果。文献[12]基于整数阶Hopfield神经网络模型提出了分数阶Hopfield型神经网络模型，并引起了人们对分数阶Hopfield型神经网络的稳定性及特殊结构的动力行为等方面的广泛关注[13-15]。

本文研究了分数阶Hopfield型神经网络的全局渐近稳定性，得到了一种LMI形式的充分条件，并通过实例仿真验证了结论的正确性。

1 预备工作

定义1：[1-2]如果 f(t)∈C1(0,+∞)，那么称

为函数 f()

定义2：[1-2]如果 f(t)∈C1(0,+∞)，那么称

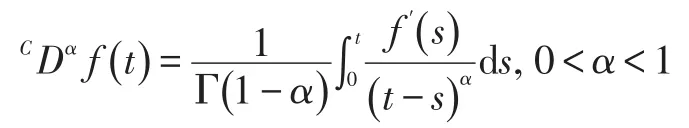
为函数 f(t)的α阶Caputo型分数阶导数。

为简便起见，下文将α阶Caputo导数记为Dα。由文献[1]知，Dα的Laplace变换式为

定义3：[1-2]Mittag-Leffler函数的单参数和双参数分别定义为：

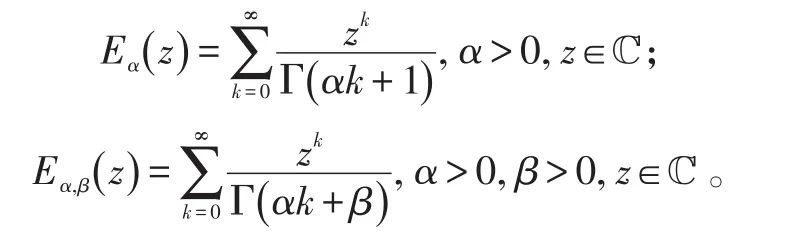
由文献[1]知，双参数Mittag-Leffler函数的Laplace变换式为：

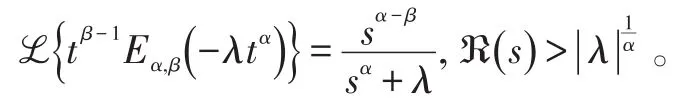
考虑如下分数阶神经网络：

式（1）的向量形式为：

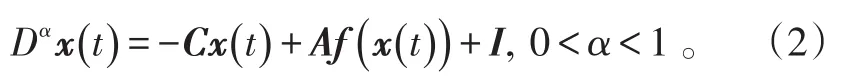
为研究分数阶系统的稳定性，需要下面假设及引理。

假设1：激励函数 fi(·)(i=1,2,…,n)有界，且满足Lipschitz条件，即存在Lipschitz常数li使得

引理1：[1-2]Caputo导数Dα具有以下性质：

1）Dαc=0，这里c为常数；

2）Dα(μf(t)+νg(t))=μDαf(t)+νDαg(t)，其中μ、ν为常数。

引理3：[16]假定x(t)∈为连续可微的向量函数，则对任意t≥t0，存在对称正定方阵P使得下式成立：

2 主要结果

定理1：若存在对称正定方阵P，正对角矩阵Γ=diag[γ1,γ2,…,γn]＞0，使得下面LMI成立：

则系统是全局渐近稳定的。

显然F(0)=0。因此，为研究系统（1）的稳定性，只需研究系统（5）零解的稳定性。

下面构造函数

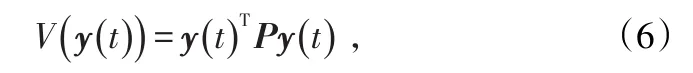
其中矩阵P满足引理3，则

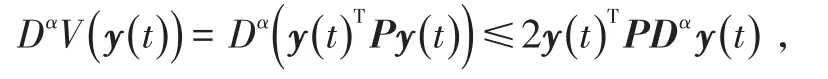
进一步，

3 实例仿真

为系统（1）选取参数

通过Matlab软件LMI工具包进行求解，结果显示LMI条件是可行的，可行解如下：

根据定理1可知系统是全局渐近稳定的，图1～3分别为x1(t)、x2(t)、x3(t)随时间t(s)收敛于0的趋势图。

图1 x1(t)随时间t收敛于0的趋势图Fig.1 Tendency chart ofx1(t)converging to 0 witht

图2 x2(t)随时间t收敛于零的趋势图Fig.2 Tendency chart ofx2(t)converging to 0 witht

图3 x3(t)随时间t收敛于零的趋势图Fig.3 Tendency chart ofx3(t)converging to 0 witht

4 结论

本文通过对分数阶Hopfield型神经网络进行全局渐近稳定性分析，给出了判定该类系统全局渐近稳定性的LMI条件，并进行了Matlab仿真，通过实例验证了文中定理的正确性。

[1]PODLUBNY I.Fractional differential equations：an introduction to fractional derivatives，fractional differential equations，to methods of their solution and some of their application[M].New York：Academic Press，1998：78-81.

[2]KILBASAA，SRIVASTAVAH M，TRUJULLO J J.Theory and applications of fractional differential equations [M].Amsterdam：Elsevier Science Limited，2006：90-99.

[3]LAKSHMIKANTHAM V，VATSALA A S.Basic theory of fractional differential equations[J].Nonlinear Analysis：Theory，Methods andApplications，2008，69：2677-2682.

[4]LAKSHMIKANTHAM V.Theory of fractional functional differential equations[J].Nonlinear Analysis：Theory，Methods andApplications，2008，69：3337-3343.

[5]AGARWAL R P，LAKSHMIKANTHAM V，NIETO J J. On the concept of solution for fractional differential equations with uncertainty[J].Nonlinear Analysis：Theory，Methods andApplications，2010，72：2859-2862.

[6]LI C，CHEN A，YE J.Numerical approaches to fractional calculus and fractional ordinary differential equation[J]. Journal of Computational Physics，2011，230：3352-3368. [7]MOROGADO M L，FORD N J，LIMA P M.Analysis and numerical methods for fractional differential equationswith delay[J].Journal of Computational and Applied Mathematics，2013，252：159-168.

[8]ZHAO Y G，WANG Y Z，LIU Z B.Finite time stability analysis for nonlinear fractional order differential systems [C]//The 32ndChinese Control Conference.Xi’an：IEEE CPP，2013，487-492.

[9]LIAO Z，PENG C，LI W，WANG Y.Robust stability analysis for a class of fractional order systems with uncertain parameters[J].Journal of the Franklin Institute，2011，348：1101-1113.

[10]LI Y，CHEN Y，PODLUBNY I.Mittag-leffler stability of fractional order nonlinear dynamic systems[J].Automatica，2009，45：1965-1969.

[11]LI Y，CHEN Y，PODLUBNY I.Stability of fractional-order nonlinear dynamic systems：Lyapunov direct method and generalized Mittag-Leffler stability[J].Computers and Mathematics withApplications，2010，59：1810-1821.

[12]BOROOMAND A，MENHAJ M B.Fractional-order hopfield neural networks[J].Advances in Neuro-Information Processing，2009，5506：883-890.

[13]KASLIK E，SIVASUNDARAM S.Nonlinear dynamics and chaos in fractional-order neural networks[J].Neural Networks，2012，32：245-256.

[14]CHEN L，CHAI Y，WU R，et al.Dynamic analysis of a class of fractional-order neural networks with delay[J]. Neurocomputing，2013，111：190-194.

[15]ZOU T，QU J，CHEN L，et al.Stability analysis of a class of fractional-order neural networks[J].Telkomnika Indonesian Journal of Electrical Engineering，2014，12：1086-1093.

[16]MANUEL A DUARTE-MERMOUD，N AGUILA-CAMACHO，JAVIER A GALLEGOS，et al.Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems[J].Commun Nonlinear Science Numer Simulat，2015，22：650-659.

Global Asymptotically Stability of Fractional-Order Hopfield Neural Networks

CUI Shiweia,GAI Mingjiub,LIU Xiaoleib
（Naval Aeronautical and Astronautical University a.Graduate student’Brigade; b.Department of Basic Sciences,Yantai Shandong 264001,China）

In this paper,the global asymptotically stability of fractional-order hopfield neural networks was investigated, and a sufficient condition was given by using LMI approach.At last,a numerical example and corresponding numerical simulation were presented to demonstrate the effectiveness of the result.

fractional order;neural networks;asymptotically stability;LMI

O175.13

A

1673-1522（2015）05-0493-04

10.7682/j.issn.1673-1522.2015.05.019

2015-05-10；

2015-07-20

崔世维（1990-），男，硕士生。