高斯模糊下舰船图像的矩特征

张 海，于吉红

（海军航空工程学院指挥系，山东烟台264001）

高斯模糊下舰船图像的矩特征

张 海，于吉红

（海军航空工程学院指挥系，山东烟台264001）

针对舰船目标图像受到自身运动、环境和图像预处理的影响出现模糊，丢失轮廓信息，造成像素点阵模糊和矩特征变化的问题，在高斯模糊低阶矩特征分析的基础上，提出并证明了Hu矩、仿射不变矩特征在高斯模糊作用下的变化定理；通过2个仿真实验验证了定理的正确性；为了保证舰船目标的识别效率，提出了建立多尺度特征库的建议。

目标识别；矩特征；高斯模糊；多尺度

基于不变矩特征的舰船目标识别，必须先找到感兴趣区域，在感兴趣区域计算不变矩特征，然后识别目标类型。由于成像过程的环境影响和图像预处理的影响，待识别舰船图像往往比较模糊，尤其在目标尺寸很小的情况下目标的轮廓信息丢失，造成图像的像素点阵模糊，这种模糊过程可用高斯卷积近似[1-2]，此时图像的矩特征一般也会发生变化。因此，有必要研究舰船图像在模糊情况下的矩特征变化规律，以提高目标识别的效率。Hu矩、仿射不变矩的计算公式由不大于4阶的矩多项式组成，Flusser[3-4]构造了中心对称点扩展函数模糊作用下的中心矩和光照不变矩，但没有给出模糊前后矩之间的关系式以及具体的变化情况。本文研究了低阶Hu矩、仿射不变矩特征在高斯模糊函数作用下的变化规律。

1 高斯模糊下低阶矩特征

成像传感器由近及远获取目标图像时，分辨率变差，产生模糊，该模糊过程是高斯点扩展函数作用的结果。令原图像为 f(x,y)，目标所在区域为D，高斯模糊过程的数学模型为[2，5]：

式（1）中：⊗表示卷积运算；

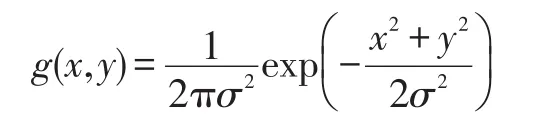
为二维高斯点扩展函数，(x2+y2)称为模糊半径，σ为标准偏差。

高斯点扩展模糊在减小图像尺寸时出现，相当于对图像进行欠采样。低阶矩特征的变化规律为[1，6-7]：高斯模糊不改变目标图像的奇数阶中心矩，当p+q为奇数时，高斯模糊下图像的中心矩不变，且图像的零阶原点矩m00、零阶中心矩 μ00和质心（xˉ=m10/m00，yˉ=m01/m00）保持不变。

1.1 高斯模糊下Hu矩特征

Hu矩表达式由①～⑨的子项组成[5，7-8]：①η11；②η20+η02；③η20-η02；④η21+η03；⑤η03-3η21；⑥η30-η12；⑦η30+η12；⑧η30-3η12；⑨3η30+η12。其中，ηij表示标准化中心矩，由低阶矩特征变化规律有定理1成立。

定理1：高斯模糊下第1个Hu矩特征值发生变化，增加量为2σ2/μ00，其他6个矩特征值不变。

证明：首先计算9个子项在高斯模糊作用下的表达式，发现除了前3项为偶数阶矩外，其余6项均由奇数阶矩，由文献[1，5]可知，子项①～③保持不变，第④～⑨子项变为：

①η′11=η11；

②η′20+η′02=η20+η02+2σ2/μ00；

③η′20-η′02=η20-η02。

高斯模糊作用下，除φ1增加2σ2/μ00外，其余Hu矩表达式保持不变，依然保持平移旋转尺度（TRS）不变性，定理得证。

Hu矩第1个表达式变化为：φ′1=φ1+2σ2/μ00，μ00表示目标图像的零阶中心矩，由中心矩、原点矩定义有 μ00=m00成立，即 μ00表示目标图像的面积，满足μ00＞0，尺度越大面积越小；反之，面积越大。σ为高斯模糊函数的标准偏差，与成像系统有关，当尺度确定时，φ1与σ2满足线性函数关系，通过迭代算法可以实现对φ1的修正。

1.2 高斯模糊下仿射不变矩

仿射不变矩[3，9]在高斯模糊作用下几乎都发生了改变，有定理2成立。

定理2：高斯模糊作用下仿射不变矩将发生变化，第2个仿射不变矩表达式除外。

证明：令高斯模糊作用下目标图像的仿射不变矩为I′i，由低阶矩特征变化规律可得：

1）由第2个仿射不变矩表达式可知，高斯模糊不改变其大小。

2）对第1个仿射不变矩表达式，

3）对第3个仿射不变矩表达式，因为高斯模糊不改变奇数阶中心矩，清楚起见，令则：

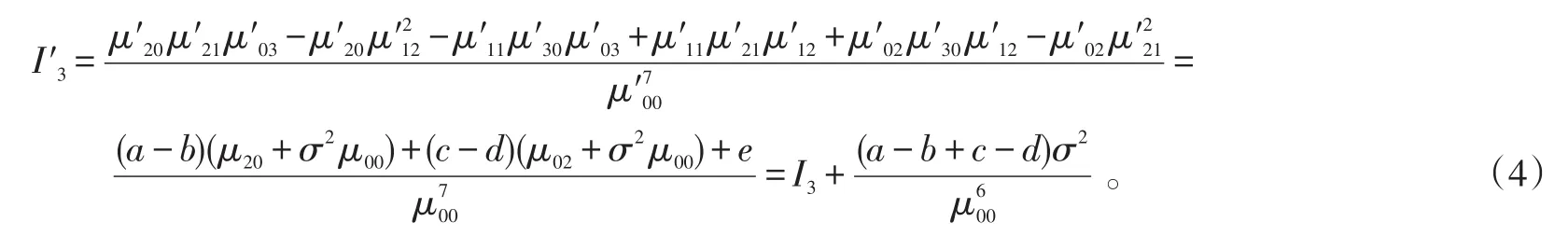
4）同3）推导方法，其他仿射不变矩表达式都将发生变化。定理得证。

2 离散化矩特征

事实上，成像系统获得的图像是离散的，矩特征也是定义在离散情况下。

假设目标图像的长宽分别为M和N，离散图像的原点矩、中心矩定义为[5，7，10]：

高斯模糊作用下目标图像的原点矩和中心矩表示为：

目标图像的离散化反映了矩值围绕真实值上下波动的信息，ΔxΔy取为整数值1时，引入了积分误差，矩阶数和次数越高不变矩特征值偏离理想矩值越远。图像分辨率高时误差相对较小，分辨率低时积分误差较大，最终影响矩值的大小，当Δx→0，Δy→0时，上式的极限值代表精确的中心矩。

3 仿真实验

3.1 实验一

本实验研究单一尺度高斯模糊下的矩特征变化，假设摄像机焦距不变，距离目标的距离不变，仅存在镜头抖动。令俯仰角为 ρ∈[0°,90°]，航向角为θ∈[0°,360°)，随机选取某型护卫舰2个视点图像，见图1，分辨率为256×256。图像因摄像机抖动产生的模糊用高斯模糊近似，分别计算图像的低阶中心矩，为防止矩值过小和出现负值的情况，仿真计算时取对数的绝对值，且保留到小数点后两位（表1）。为便于观察比较，将视点图像的2～5阶中心矩值表示成柱状图，篇幅原因仅给出视点1图像的中心矩比较，见图2。其中左边的白色柱状图表示原始图像中心矩，右边的灰色柱状图表示高斯模糊后图像中心矩，可以看出奇数阶的中心矩值几乎不变，偶数阶的中心矩值有轻微变化，但变化范围很小，不超过2%。

图1 某型舰船的2个视点图像Fig.1 Views of some type of ship

表1 低阶中心矩值Tab.1 Results of low order centeral moments

图2 视点1原始图像和模糊图像的柱状图Fig.2 Histogram of original image and blurred image of view one

矩值产生小范围波动是由于积分区间有限造成的，低阶矩变化规律的推导是理想模糊作用下的积分形式（目标所在区域为D∈(-∞,+∞)）[1，5]，实际使用中积分区间是有限的D′，模糊后中心矩的表示变成：

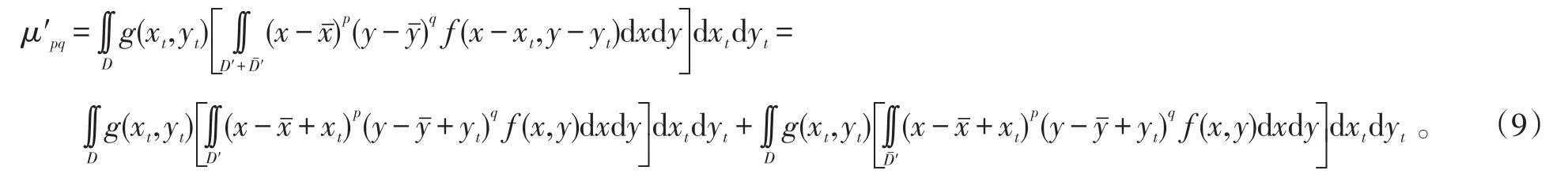
式（9）中：第1项是真实的中心矩，第2项产生矩值波动的误差，因为舰船目标所占区域面积D′不固定，第2项多项式的值一般不为0，因而中心矩值会产生一定的波动，其中D′+Dˉ′=D。进一步，根据中心矩计算的Hu矩和仿射矩也会产生误差，图1的Hu矩和仿射不变矩结果见0，可以看出Hu矩基本不变，在±0.5内波动，仿射矩变化相对较大，证明定理1和定理2的正确性，Hu矩和仿射矩结果见表2。

表2 Hu矩和仿射矩结果Tab.2 Results of Hu moments and affine moments

3.2 实验二

该实验的目的是研究高斯模糊下多尺度矩特征情况，当舰船远离摄像机时，舰船目标面积逐渐减小。图3所示为实验一中护卫舰图像的多尺度图像，保持矩特征积分区域不变（图像的大小始终为256×256），目标面积逐级减小为上一级的1/2。

图3 多尺度图像Fig.3 Multi-scale images

为清楚表现不同尺度下矩特征的变化，按特征值取值范围分别画出各尺度图像的Hu矩和仿射矩如图4～5所示。

除了φ5、φ7外其他矩特征变化幅度不大。当积分区域不变，尺度变化时，大部分Hu矩特征比较稳定，而仿射矩I5、I6受尺度变化影响较大，其他矩分量仅产生了小幅度变化，相对比较稳定。

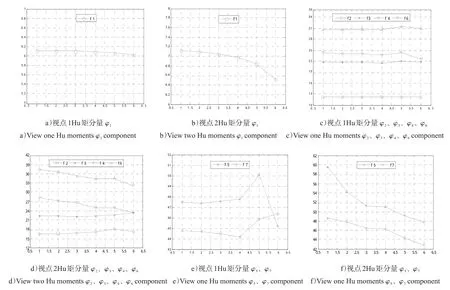
图4 Hu矩变化曲线Fig.4 Curve of Hu moments

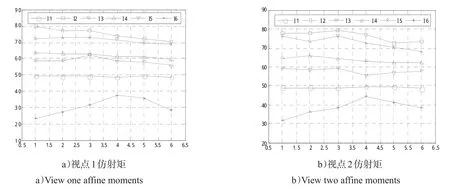
图5 仿射矩变化曲线Fig.5 Curve of affine moments

4 结论

舰船在实际成像过程会受到各种因素影响，使得实际图像模糊。本文从理论上推导了这种模糊情况下的图像Hu矩、仿射矩特征的变化规律，并用仿真实验验证了特征变化规律的合理性。

为提高后续目标识别的效率，有必要针对舰船目标的不同尺度图像提取特征，例如：令第1级尺度图像大小为size=1，第2级尺度图像大小为size=1/2，第3级尺度图像大小为size=1/4，…，分别计算舰船目标的5级尺度不变矩特征，建立其多尺度特征库，以提高识别目标的效率。

[1]张天序.成像自动目标识别[M].武汉：湖北科学技术出版社，2005：18-21. ZHANG TIANXU.Automated recognition of imaged targets[M].Wuhan：Hubei Science and Technology Press，2005：18-21.（in Chinese）

[2]高志升，谢春芝.具有高斯噪声不变性的特征描述算子[J].计算机工程与应用，2011，47（31）：4-6. GAO ZHISHENG，XIE CHUNZHI.Gaussian noise insensitive image feature descriptor[J].Computer Engineering andApplications，2011，47（31）：4-6.（in Chinese）

[3]FLUSSER J，SUK T.Pattern recognition by affine moment invariants[J].Pattern Recognition，1993，26：167-174.

[4]JAN FLUSSER.Moment invariants in image analysis[J]. World Academy of Science，Engineering and Technology，2005，11：376-382.

[5]HU M K.Visual pattern recognition by moment invariants [J].IEEE Transactions on Information Theory，1962，8（2）：179-187.

[6]张天序，刘进.目标不变矩的稳定性研究[J].红外与毫米波学报，2004，23（3）：197-200. ZHANG TIANXU，LIU JIN.Investigation on the stability of object moment invariants[J].Journal of Infrared and Millimeter Waves，2004，23（3）：197-200.（in Chinese）

[7]刘进，张天序.图像不变矩的轮廓链快速算法[J].华中科技大学学报：自然科学版，2003，31（1）：67-69. LIU JIN，ZHANG TIANXU.A fast moment algorithm based on link points around shape[J].Journal of Huazhong University of Science and Technology：Natural Science Edition，2003，31（1）：67-69.（in Chinese）

[8]杨静，丘江，王岩飞，等.线性不变矩及其在图像识别中的应用算法研究[J].光子学报，2003，32（3）：81-84. YANG JING.QIU JIANG，WANG YANFEI，et al.Research of line moments and its application in image boundaries recognition[J].Acta Photonica Sinica，2003，32（3）：81-84.（in Chinese）

[9]HEIKKILA J.Pattern matching with affine moment descriptors[J].Pattern Recognition，2004，37：1825-1834.

[10]CORDELIA SCHMID，ROGER MOHR.Local gray value invariants for image retrieval[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，19（5）：530-535.

Moment Features of Ship Image under Gaussian Blur

ZHANG Hai,YU Jihong
（Department of Command,NAAU,Yantai Shandong 264001,China）

Ship target images appear blurring;lose contour information for the reasons of movement,environment and im⁃age preprocessing.All of these result in blurring pixel and moment features changing.Based on the Gaussian blur feature analysis of the lower order moments,Hu moment and affine invariant moment features change theorems were proposed. Through both theoretical analysis and simulation experiments the correctness of these theorems was verified.Finally,the suggestion to establish a multi-scale features database for the recognition rate of ship targets was proposed.

target recognition;moment features;gaussian blur;multi-scale

TP391.41

A

1673-1522（2015）05-0479-05

10.7682/j.issn.1673-1522.2015.05.016

2015-05-20；

2015-07-29

张 海（1973-），男，讲师，博士。