空时分组码的二阶循环平稳特性分析

闫文君，张立民，凌 青，孔东明

（1.海军航空工程学院a.电子信息工程系；b.信息融合所，山东烟台264001；2.海军装备部，太原030027）

空时分组码的二阶循环平稳特性分析

闫文君1a，张立民1b，凌 青1a，孔东明2

（1.海军航空工程学院a.电子信息工程系；b.信息融合所，山东烟台264001；2.海军装备部，太原030027）

针对空时分组码的盲识别问题，研究空时分组码信号的二阶循环平稳特性。利用空时分组码矩阵元素之间的相关性，给出了空时分组码相关矩阵的傅里叶变换形式，推导出空时分组码信号在不同时延参数下具有循环频率的特征。通过仿真实验，验证了推导过程的正确性，并定义了用于空时分组码识别的决策树，对空时分组码盲识别技术的发展进行了展望。

信号处理；空时分组码；二阶循环平稳

近年来，随着无线通信技术发展，无线系统中信息的传输数量和传输速率越来越大，给无线通信技术带来了巨大的挑战。一个满足传输信息数量增多、传输速率加快的需求的重要技术就是多输入多输出系统（Multiple Input Multiple Output，MIMO）[1]。MIMO系统中，不可避免地存在时变多径衰落问题，解决有效手段之一就是天线分集技术[2]。利用天线分集的方法有发射分集和接收分集。接收分集可获得很大的性能增益，它不仅有较好的链路预算资源，而且具有更强的抗邻道干扰能力。来自不同接收天线的信号通常是通过数字硬件进行合并，其性能增益与分集效果相关，分集效果受不同天线不同路径的信号之间的衰落的相互独立性影响。当今很多通信系统的基站都是采用接收分集。例如全球移动通信系统（GSM）[2]的基站通常采用2根接收天线。然而，由于接收端功率、天线尺寸和成本的限制，在接收端通常不能实现任意增加天线。发射分集是在发射端增加发射天线，它可以改善整个无线通信系统的通信质量而不需要每个接收者改善设备，这对于通信网络运营商负担不大，接收端用户也乐于接受。增加基站复杂度，减少接收端复杂度也是未来无线通信系统发展的要求[3]。

空时分组码（Space-Time Block Code，STBC）是随着分集技术的发展而出现的一种非常有效的信道编码方式[4]。空时分组码盲识别技术是一个新的重要的信号处理方向。如图1所示，识别的问题主要有：发射天线数识别[5]、调制方式识别[6-8]、正交识别[9]和类型识别[10-23]4个方面。其中，空时分组码类型识别分为基于最大似然的算法（Maximum Likelihood，ML）[10]和基于特征参数（Feature Based，FB）的算法。FB算法又分为基于高阶统计量的算法[11-14]和基于二阶相关特性的算法[15-23]。图2为空时分组码类型识别算法分类。基于最大似然的算法能够得到局部最优解，识别效果较好，但识别之前需要知道传输信号的信道信息、噪声信息和调制信息，且计算复杂度较高。基于特征参数的算法识别前不需要知道传输信号的信道信息、噪声信息和调制信息，计算复杂度较低。在实际系统中可根据系统状况合理选择识别方法。

图1 空时分组码识别问题分类Fig.1 Category of classification for STBC

图2 空时分组码识别算法Fig.2 Classification alaorithm for STBC

本文对空时分组码的二阶循环平稳特性进行分析，二阶循环平稳特性算法属于基于二阶相关特性的算法，通过建立接收信号的二阶循环平稳模型，可对不同空时分组码进行识别。

1 空时分组码

给定一个具有nt个发射天线、nr个接收天线的具有空时分组码的线性通信系统，设每个空时分组码矩阵传输符号数为ne，各符号之间独立同分布，经历的时间间隔数为L，则第k个码矩阵传输的符号为Sk=[sk(1),sk(2),…,sk(ne)]，则空时分组码码矩阵是nt×L维矩阵，表示为Cu(Sv)，其中u和v表示空时分组码的第v个传输块的第u列，其中0＜u≤L。

空时分组码类型很多，一般文献常涉及的用于识别的典型空时分组码有以下4种。

SM（Spatial Multiplexing，空间复用）：发射天线数为nt=j，码矩阵长度L=1[8]，

严格的讲，SM并非空时分组码。

AL（Alamouti STBC）：发射天线数为nt=2，码矩阵长度L=2[4]，

STBC3：发射天线数nt=3，码矩阵长度L=4[9]，

STBC4：发射天线数nt=3，码矩阵长度L=8[9]，

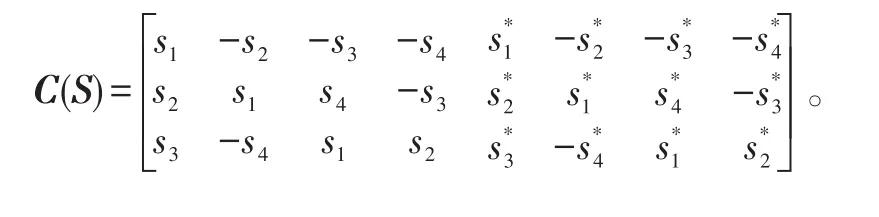
2 基于二阶循环平稳的算法

通过空时分组码矩阵可以看出，在一个空时分组码内，不同列之间的符号是相关的，而不在一个空时分组码内的不同列之间的符号是无关的。这在频域上将表现出不同的循环谱和循环频率。使用基于二阶循环平稳的算法的前提就是寻找接收信号的四阶循环谱的循环频率。定义接收信号为[23]：

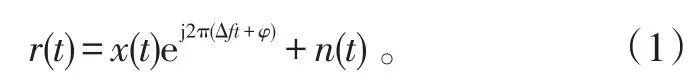
式（1）中：t为符号周期T0内一点；Δf为载波频偏；φ为相位偏移和相位噪声；n(t)为加性高斯噪声信号，噪声信号之间相互独立，且与接收信号相互独立；x(t)为第t时刻传输信号，且有[23]：

式（2）、（3）中：hi(t)代表第i个发射天线的信道系数；n为整数（本文中如无特殊说明均如此定义）；(t)表示为g(t-(k+l-1)T+ε)；g(t)是发射端整形滤波器和接收端滤波器的级联；T为符号周期；ε代表发射滤波器和接收滤波器的时延；Ci,l代表编码矩阵的第i行第l列元素，0＜i≤nt、0＜l≤L，且i和l必须是整数。

接收信号的二阶时变自相关函数定义为[15]

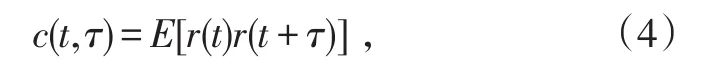
式中，τ为时延参数。

接收信号二阶时变自相关函数c(t,τ)的傅里叶变换为[23]

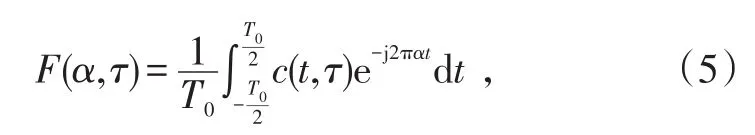
式中，α为时变自相关函数的循环频率。

SM信号之间互不相关，因而SM信号不具有循环频率。因此

由式（8）可以观察到cAL(t,τ)是周期为2T的周期函数，式（7）可以进一步写为：

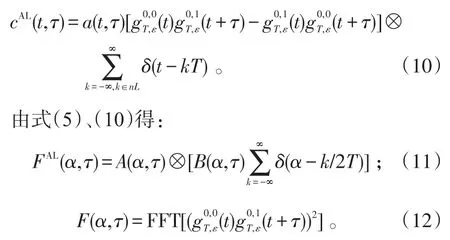
式（11）、（12）中，A(α,τ)是a(t,τ)的傅立叶变换。

如A(α,τ)与α相互独立，显然可得到FAL(α,τ)具有1/2T的整数倍的循环频率。STBC3和STBC4的推导过程同理可得，本文不再进行推导。

3 实验验证

本节对本文提出的算法进行验证，假定接收天线数为2，信号数为8 192，信号经过QPSK调制，信道采用Nakagami-m衰落信道，信道参数m=3，噪声采用高斯白噪声，信噪比取-10dB。取不同时延参数τ∈{1,2,4}进行仿真，见图3～5。

图3 τ=1时，接收信号功率谱Fig.3 Power spectrum of received signals withτ=1

图4 τ=2时，接收信号功率谱Fig.4 Power spectrum of received signals withτ=2

图5 τ=4时，接收信号功率谱Fig.5 Power spectrum of received signals withτ=4

由图3～5可得，当时延参数τ=4时，只有STBC4具有循环频率；若排除STBC4，当时延参数τ=2时，只有STBC3具有循环频率；当时延参数τ=1时，只有AL具有循环频率，剩下的信号就是SM信号。该识别过程可用如图6所示决策树表示，其中，“是”表示具有循环频率，“否”代表不具有循环频率。

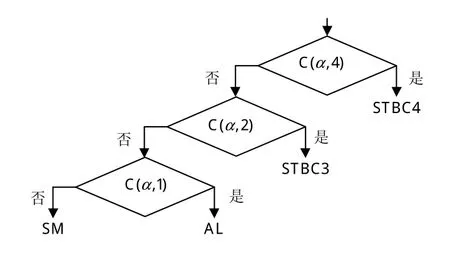
图6 空时分组码识别决策树Fig.6 Decision tree of classification for STBC

4 总结和展望

本文在全盲条件下对空时分组码识别中二阶循环平稳的算法进行了分析，该方法具有不需要预先估计信道、噪声和调制方式的特点，经过仿真，算法能明显区分不同STBC信号，在工程实现上具有很大的可行性。

作为无线通信领域一个新的重要研究内容，空时分组码的识别应重点关注：①接收天线数较少，甚至只有一根接收天线下空时分组码盲识别问题，增大基站复杂度减少接收端复杂度是未来无线通信发展的必然要求；②OFDM与空时分组码的结合条件下的空时分组码盲识别；③STBC信号的调制识别算法。

[1]DOBRE OA，ABDI A，BAR-NESS Y，et al.A survey of automatic modulation classification techniques：classical approaches and new developments[J].IET Communications，2007，1（2）：137-156.

[2]LARSSON EG，STOICA P.Space-time block coding for wireless communications[M].任品毅，译.西安：西安交通大学出版社，2006：1-4. LARSSON EG，STOICA P.Space-time block coding for wireless communications[M].Ren Pinyi，translated.Xi’an：Xi’an Jiaotong University Press，2006：1-4.（in Chinese）

[3]DOBRE OA.Signal identification for emerging intelligent radios：classical problems and new challenges[J]. IEEE Instrumentation&Measurement Magazine，2015，18（2）：11-18.

[4]ALAMOUTI SM.A simple transmit diversity technique for wireless communications[J].IEEE Journal on SelectedAreas in Communications，1998，16（8）：1451-1458.

[5]SHI M，BAR-NESS Y，SU W.Adaptive estimation of the number of transmit antennas[C]//IEEE Global Telecommunications Conference.Orlando，FL：IEEE，2007：3034-3039.

[6]MAREY M，DOBRE OA.Blind modulation classification algorithm for single and multiple-antenna systems over frequency-selective channels[J].IEEE Signal Processing Letters，2014，21（9）：1098-1102.

[7]PANAGIOTOU P，ANASTASOUPOULOS A，POLYDOROS A.Likelihood ratio tests for modulation classification[C]//21stCentury Military Communications Conference Proceedings.Los Angeles，CA：IEEE，2000：670-674.

[8]HAMEED F，DOBRE OA，POPESCU DC.On the likelihood-based approach to modulation classification[J]. IEEE Transactions on Wireless Communications，2009，8（12）：5884-5892.

[9]赵知劲，谢少萍，王海泉.OSTBC信号累积量特征分析[J].电路与系统学报，2013，18（1）：150-155. ZHAO ZHIJIN，XIE SHAOPING，WANG HAIQUAN. The characteristic analysis of cumulants of the OSTBC signals[J].Journal of Circuits and Systems，2013，18（1）：150-155.（in Chinese）

[10]CHOQUEUSE V，MARAZIN M，COLLIN L，et al.Blind recognition of linear space time block codes：a likelihoodbased approach[J].IEEE Transactions on Signal Processing，2010，58（3）：1290-1299.

[11]ELDEMERDASH YA，MAREY M，DOBRE OA，et al. Fourth-order statistics for blind classification of spatial multiplexing and alamouti space-time block code signals [J].IEEE Transaction on Communications，2013，61（6）：2420-2431.

[12]CHOQUEUSE V，MANSOUR A，BUREL G，et al.Blind channel estimation for STBC system using higher-order statistics[J].IEEE Transactions on Wireless Communications，2011，10（2）：495-505.

[13]ELDEMERDASH YA，DOBRE OA，MAREY M，et al. An efficient algorithm for space-time block code classification[C]//IEEE Global Communications Conference.Atlanta，GA：IEEE，2013：3329-3334.

[14]DEYOUNG M，HEALTH R，EVANS BL.Using higher order cyclostationarity to identify space-time block codes [C]//IEEE Global Telecommunications Conference.New Orleans，LO：IEEE，2008：3370-3374.

[15]CHOQUEUSE V，YAO K，COLLIN L.Hierarchical space-time block code recognition using correlation matrices[J].IEEE Transactions on Wireless Communications，2008，7（9）：3526-3534.

[16]CHOQUEUSE V，YAO K，COLLIN L，BUREL G.Blind recognition of linear space time block codes[C]//Proc. IEEE International Conference Acoustics Speech and Signal Processings.Las Vegas：IEEE，2008：2833-2836.

[17]MAREY M，DOBRE OA，LIAO B.Classification of STBC system over frequency-selective channels[J].IEEE Transactions on Vehicular Technology，2015，64（5）：2159-2164.

[18]QIAN G，LI L，LUO M，et al.Blind recognition of spacetime block code in MISO system[J].Journal on Wireless Communications and Networking，2013（6）：201-205.

[19]LUO M，GAN L，LI L.Blind recognition of space-time block code using correlation matrices in a high dimensional feature space[J].Journal of Information&Computational Science，2012，9（6）：1469-1476.

[20]MOHAMMADARIMI M，DOBRE O.A.Blind identification of spatial multiplexing and Alamouti space-time block code via Kolmogorov-Smirnov（K-S）test[J].IEEE Communications Letters，2014，18（10）：1711-1714.

[21]MAREY M，DOBRE OA，INKOL R.Classification of space time block codes based on second-order cyclostationarity with transmission impairments[J].IEEE Transaction on Wireless Communication，2012，11（7）：2574-2584.

[22]KARAMI E，DOBRE OA.Identification of SM-OFDM and AL-OFDM signals based on their second-order cyclostationarity[J].IEEE Transactions on Vehicular Technology，2015，64（3）：942-953.

[23]MAREY M，DOBRE OA，INKOL.Cyclostationaritybased blind classification of STBCs for cognitive radio systems[C]//IEEE International Conference on Communications.Ottawa ON：IEEE，2012：1715-1720.

Characteristic Analysis of Blind Classification for STBC Based on Second-Order Cyclostationarity Statistics

YAN Wenjun1a,ZHANG Limin1b,LING Qing1a,KONG Dongming2
（Naval Aeronautical and Astronautical University a.Department of Electronic and Information Engineering; b.Institute of Information Fusion,Shandong Yantai 264001,China; 3.Naval Equipment Department,Taiyuan 030027,China）

In the light of the problem of blind classification for space-time block coding(STBC),the second-order cyclosta⁃tionarity statistics were analyzed.Using the correlation of the elements in STBC matrix,the Fourier coefficients were de⁃fined,and the characters that signals of STBC have cycle frequencies was proved.Simulation showed the validity of the der⁃ivation,and the decision tree was made for classification.And finally,the proposed algorithms were summarized and the fu⁃ture development of classification of STBC was pointed out.

signal processing;space-time block bode;second-order cyclostationarity

TN911.7

A

1673-1522（2015）05-0409-05

10.7682/j.issn.1673-1522.2015.05.002

2015-06-07；

2015-08-11

国家自然科学基金资助项目（61102167）

闫文君（1986-），男，博士生。