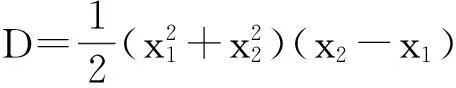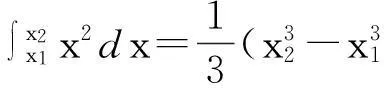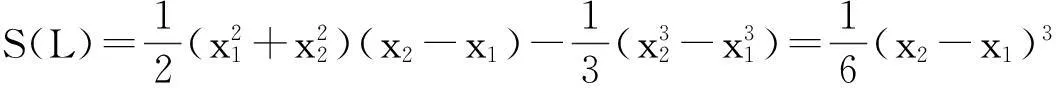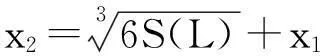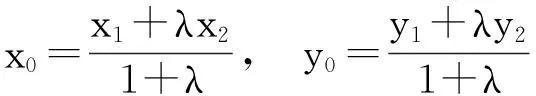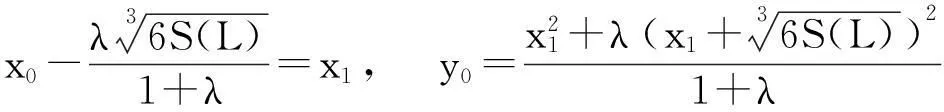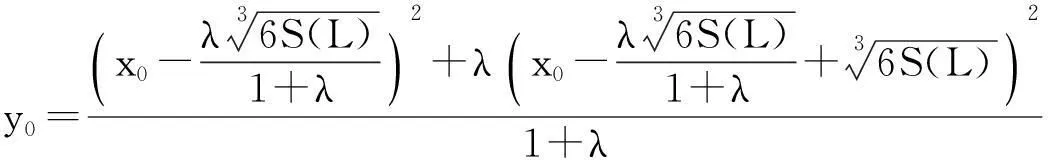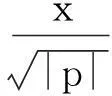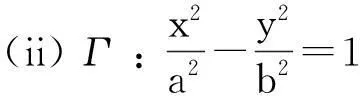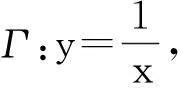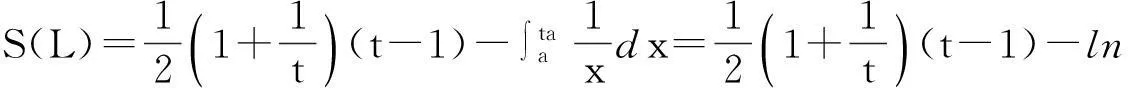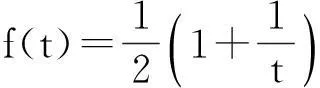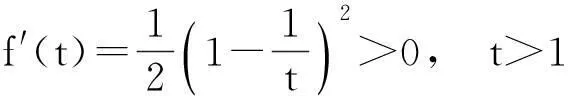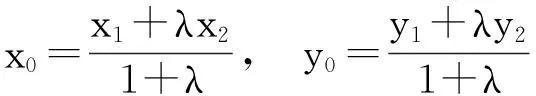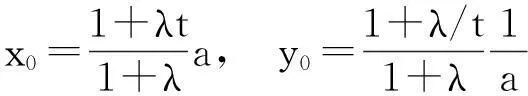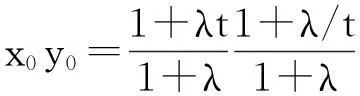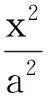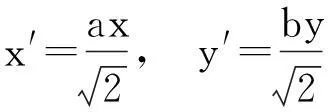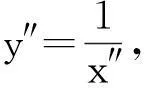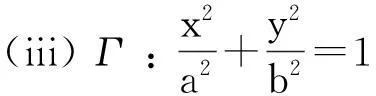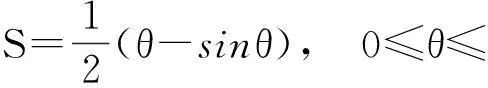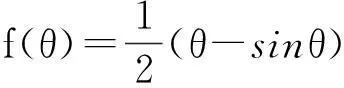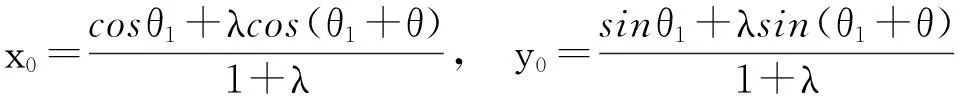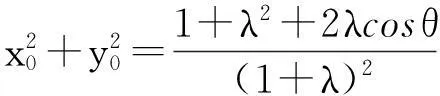直线与圆锥曲线围成定面积其弦上定比例点的轨迹

舒阳春

(武汉科技大学国际学院，武汉430081)

直线与圆锥曲线围成定面积其弦上定比例点的轨迹

舒阳春

(武汉科技大学国际学院，武汉430081)

[摘要]通过一个大学数学竞赛题的推广，证明了一直线与圆锥曲线所围成定面积时，其弦上定比例点的轨迹与原圆锥曲线是同一类型的曲线.

[关键词]圆锥曲线； 定面积； 轨迹

本文讨论的内容来源于全国大学生数学竞赛(第四届全国大学生数学竞赛决赛(专业组)试卷，题1，2013)，原题是这样的：

设A为一正数，直线L与双曲线x2-y2=2(x>0)所围成的面积为A,

(i) 上述L被双曲线所截线段的中点的轨迹为双曲线.

我们发现上述问题的结论可以推到任何双曲线及椭圆和抛物线的情况并且不仅对于弦的中点的轨迹是与原曲线同类型，而且得到了对于定比例点的轨迹也都具有与原圆锥曲线相同的类型.本文主要借助于解析几何中的仿射变换把所讨论的曲线化为标准型从而再利用微积分的方法得到这个推广的结果，细述如下：

定理设Γ是一平面圆锥曲线(圆，抛物线，椭圆之一)，Γ的一般形式为

Ax2+Bxy+Cy2+Dx+Ey+F=0(常数A,B,C不全为0)

(1)

设直线L与曲线Γ相交于两个点P,Q并位于Γ 一个焦点的同一侧. 用S(L) 表示曲线Γ与线段PQ所围成的面积，R是线段PQ上的点并满足PR/RQ=(常数).如果L移动时，S(L) 是一个常数，则R的轨迹与Γ是同一类型的圆锥曲线.

下面二个引理是解析几何中熟知的结果(参见文献[1])

引理1通过正则变换可使由(1)式定义的Γ 具有下列形式之一：

(i) y=px2，

(2)

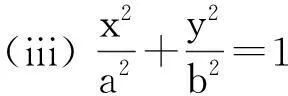
其中a,b,p是非零常数.

引理2正交变换保持圆锥曲线，直线不变，距离不变；仿射变换不改变线段比例和面积的比值及圆锥曲线的类型.

定理的证明由引理1，只需要讨论上面形状的Γ 曲线.以下分三种情况来对定理进行证明.

(i) Γ ：y=px2.

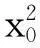
L:y=k(x-x0)+y0.

记x为L与Γ交点的横坐标， 那么x满足 x2=k(x-x0)+y0, 记两个根有关系 x1

x1+x2=k,x1x2=kx0-y0.

(3)

由直线L,x-轴 x=x1,x=x2所围成的面积为

由Γ,x-轴, x=x1,x=x2所围成的面积为

因此

(4)

解出x2得到

(5)

由于PR/RQ=,得到

(6)

将 (5) 代入 (6)式,得到

从而得

(7)

P(a, 1/a),Q(ta, 1/ta).

(8)

其中t>1.于是由L与Γ所围成的面积为

(9)

(10)

于是由连续函数的中值定理，总有唯一的实数t使得

f(t)=S(L).

取L上的点R(x0,y0) 使得PR/RQ=,有

由(8)式得

(11)

由此得

(12)

先考虑Γ ：x2+y2=1. 设直线与Γ 的两个交点表示为

P(cos(θ1+θ),sin(θ1+θ)),Q(cosθ1,sinθ1),0≤θ≤π.

(13)

那么圆与直线的所围成的面积为

(14)

可知有唯一的θ 满足f(θ)=S，再由L上的点R(x0,y0) 满足PR/RQ=, 因此，利用(13),有

(15)

因此

从而R的轨迹是一个圆.

x′2+y′2=1,

得到的结果R′ (x′,y′ ) 的轨迹是一个圆，即变换R→R′ 的像是一个圆.那么返回原坐标系知R的轨迹是一个椭圆(或圆).

结合上面的三种情况的讨论，得到了定理的证明.

[参考文献]

[1]邱维声.解析几何[M].北京：北京大学出版社:1988.154-156, 202-204, 211.

The Locus of the Point Dividing the Chord of Line Cut by the Quadratic Curve in a Given Ratio

SHUYang-chun

(International School， Wuhan University of Science and Technology, Wuhan 430081, China)

Abstract:We prove that when a line intersects a quadratic curve with the two points and the area enclosed by the line and the curve is a constant, the locus of the point of the chord of line cut by the curve in a given ratio is the same kind of curve as the original curve.

Key words:quadratic curve； constant area； locus

[中图分类号]O172

[文献标识码]C

[文章编号]1672-1454(2015)04-0120-03