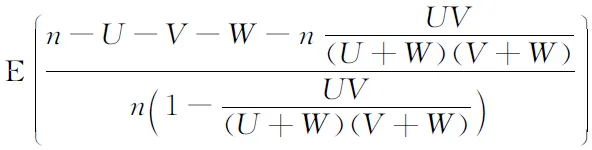二元Kundu-Gupta型二点分布参数的最大似然估计

李国安，　李建峰

(宁波大学理学院，浙江宁波315211)

二元Kundu-Gupta型二点分布参数的最大似然估计

李国安，李建峰

(宁波大学理学院，浙江宁波315211)

[摘要]讨论二元Kundu-Gupta型二点分布的识别性及参数估计，已知可识最小值的分布时，则参数可识别；由此得到了参数的最大似然估计；其中二个参数的估计量是无偏的，另外一个参数的估计量的期望不存在；模拟结果显示：估计值均稳定于真值参数.

[关键词]二元Kundu-Gupta型二点分布； 识别性； 最大似然估计； 无偏的； 模拟

1引言

众所周知，二点分布是一个收益分布，二元二点分布是一个最为基本的组合收益分布.我们在满意度市场调查研究中，获得了一个二元二点分布，从文献检索中，发现也有二元二点分布的相关文献[1-3]，其中文献[1]研究的，是一个具自然形式的二元二点分布，在本文中，意图引入文[1]研究的具自然形式的二元二点分布的特殊情形，依文[4]构造二元分布的思路，引入了一个二元Kundu-Gupta型二点分布，然后采用先参数识别后参数估计的方式，讨论了二元Kundu-Gupta型二点分布的识别性及参数估计.可以这么说：二元二点分布是所有二元分布中最为简单的分布，从教学角度来看，它是讲授二元分布之分布函数、特征函数、数字特征、乃至参数估计的一种最简单载体；从科研角度来看，参数估计是求解模型的核心问题之一，而二点分布对应的模型是绩效模型，即业绩是否达到预期之评价模型.对于二元及多元分布参数的估计，类似文献[5-18]，在已知二元及多元正态分布参数估计的情形下，还在研究二元及多元正态分布参数的识别性，因为分布参数的识别性说明分布参数的可估计性，因此，正常次序是研究分布参数识别性在先，研究分布参数估计在后.本文采用从参数的识别性进而求参数的最大似然估计路径，讨论这个二元二点分布的识别性及参数估计.在第一节，讨论了二元二点分布的识别性；在第二节，讨论了二元二点分布的参数估计.

2二元Kundu-Gupta型二点分布的识别性

二元Kundu-Gupta型二点分布定义如下：

定义1称(X,Y)服从二元一般型二点分布，是指存在三个相互独立的三个随机变量U1，U2，U3，其中

U1～B(1,p1)，U2～B(1,p2)，U3～B(1,p3)；

使得

X=max(U1,U3)，Y=max(U2,U3)，0≤p1≤1，0≤p2≤1，0≤p3≤1，

记作

(X,Y)~BBDG(1,p1,p2,p3).

记U=max(X,Y)，定义I=1,2,3分别对应于X>Y,Y>X,X=Y时，

引理1若(X,Y)~BBDG(1,p1,p2,p3)，则U的分布律为

U~B(1,1-(1-p1)(1-p2)(1-p3)).

证P(U=0) =P(X=0,Y=0)=P(max(U1,U3)=0,max(U2,U3)=0)

=P(U1=0,U2=0,U3=0)=(1-p1)(1-p2)(1-p3).

引理2若(X,Y)~BBDG(1,p1,p2,p3)，则(U,I)的联合分布律为

证P(U=0,I=3) =P(X=0,Y=0)=P(max(U1,U3)=0,max(U2,U3)=0)

=P(U1=0,U2=0,U3=0)=(1-p1)(1-p2)(1-p3)；

同理

P(U=1,I=1) =P(X=1,Y=0)=P(max(U1,U3)=1,max(U2,U3)=0)

=P(U1=1,U2=0,U3=0)=p1(1-p2)(1-p3)，

P(U=1,I=2)=P(X=0,Y=1)=P(max(U1,U3)=0,max(U2,U3)=1)

=P(U1=0,U2=1,U3=0)=p2(1-p1)(1-p3)，

P(U=1,I=3)=P(X=1,Y=1)=P(max(U1,U3)=1,max(U2,U3)=1)

=P(U3=1)+P(U1=1,U2=1,U3=0)=p3+p1p2(1-p3).

定理1设

(X,Y)~BBDG(1,p1,p2,p3)，(X′,Y′)~BBDG(1,p′1,p′2,p′3)，

若已知U与U′同分布，则所有参数皆不可识别.

证由(1-p1)(1-p2)(1-p3)=(1-p′1)(1-p′2)(1-p′3)，得所有参数皆不可识别.

定理2设

(X,Y)~BBDG(1,p1,p2,p3)，(X′,Y′)~BBDG(1,p′1,p′2,p′3)，

若已知(U,I)与(U′,I′)同分布，则所有参数皆可识别.

3二元Kundu-Gupta型二点分布的参数估计

这里，从定理2出发，直接获得了所有参数的最大似然估计.

定理3设(X,Y)~BBDG(1,p1,p2,p3)是总体，(X1,Y1),…,(Xn,Yn)是来自总体(X,Y)的容量为n的样本，记U=max(X,Y)，定义随机变量I=1,2,3分别对应于X>Y,Y>X,X=Y时；记Ui=max(Xi,Yi)，定义随机变量Ii=1,2,3分别对应于Xi>Yi,Yi>Xi,Xi=Yi时，i=1,…,n，若(U,I)具有以下的联合分布

(U1,I1),…,(Un,In)是来自总体(U,I)的容量为n的样本，则参数p1，p2，p3的最大似然估计分别为

这里

证似然函数为

并有似然方程

得

得

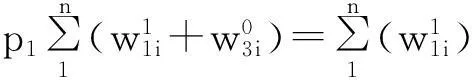
即有

代入

得

定义2称(U,V)服从二元多项分布，是指它有如下的分布律

其中0

定义3称(U,V,W)服从三元多项分布，是指它有如下的分布律

k=0,…,n-i-j，j=0,…,n-i，i=0,1,…,n，其中0

记作(U,V,W)~TBD(n,p1,p2,p3).

性质1若(U,V)~BBD(n,p1,p2)，则U~B(n,p1)，V~B(n,p2).

性质2若(U,V,W)~TBD(n,p1,p2,p3)，则

(U,V)~BBD(n,p1,p2)， (U,W)~BBD(n,p1,p3)，

(V,W)~BBD(n,p2,p3)， U~B(n,p1)，V~B(n,p2)，

W~B(n,p3).

性质4若(U,V,W)~TBD(n,p1,p2,p3)，则

不存在.

证因为W=0，U≠0，或V≠0时，出现∞项，不存在.

引理3若(X,Y)~BBDG(1,p1,p2,p3)，则

证由性质3

类似可得

证由性质4可得.

模拟分析

分别选取三组参数进行模拟，第一组：p1=0.7,p2=0.2,p3=0.1；第二组：p1=0.3，p2=0.9，p3=0.5；第三组：p1=0.4，p2=0.6，p3=0.8；都得到了估计值稳定于真值参数的结果，其中第一组参数所得的模拟结果如下：

表1　由来自二元随机变量(X,Y)~BBDG(1,p1,p2,p3)之随机数的模拟结果

实例分析

4结论

仅是Z的分布已知时，所有参数皆不可识别，当(Z,I)的分布已知时，所有参数皆可识别，即所有参数皆可估计，由此得到了参数的最大似然估计，其中二个参数的估计量是无偏的，另外一个参数的估计量的期望不存在.模拟结果显示：估计值均稳定于参数真值.

[参考文献]

[1]Marshall A W,Olkin I.A Family of Bivariate Distributions Generated by the Bivariate Bernoulli Distribution[J].J.Amer. Statist.Assoc.,1985,80(390)：332-338.

[2]Oluyede B O.A family of bivariate binomial distributions generated by extreme bernoulli distributions[J].Communica- tions in Statistics - Theory and Methods,1994,23(5)：1531-1547.

[3]Islam M A,Alzaid A A Chowdhury R I,Sultan K S.A generalized bivariate Bernoulli model with covariate dependence[J]. Journal of Applied Statistics,2013,40(5)：1064-1075.

[4]Kundu D,Gupta R D.Bivariate generalized exponential distributions[J].Journal of Multivariate Analysis,2009,100：581-593.

[5]Basu A P,Ghosh J K.Identifiability of the multinorma and other distributions under competing risks model[J].Journal of Multivariate Analysis,1978,8(3)：413-429.

[6]Hamdan M A,Nasro M O. Maximum likelihood estimation of the parameters of the bivariate binomial distribution[J].Comm. Statist. A—Theory Methods,1986,15: 747-754.

[7]Kocherlakota S.A note on the bivariate binomial distribution[J].Statist. Probab. Lett,1989, 8: 21-24.

[8]Ong S H.The computer generation of bivariate binomial variables with given marginals and correlation[J].Comm.Statist. B—Simulation Comput,1992,21: 285-299.

[9]Biswas A,Hwang J-S.A new bivariate binomial distribution[J].Statistics & Probability Letters,2002,60: 231-240.

[10]Gilliland D C,Hannan J.Identification of the Ordered Bivariate Normal Distribution by Minimum Variate[J].J. Am. Stat. Assoc. 1980,75:651-654.

[11]Mukherjea A,Stephens R.The problem of identification of parameters by the distribution of the maximum random: Solution for the trivariate normal case[J].Journal of Multivariate Analysis,1990,34(1)：95-115.

[12]Mukherjea A,Stephens R.Identification of parameters by the distribution of the maximum random variable: The general multivariate normal case [J].Probability Theory and Related Fields,1990,34(1)：289-296.

[13]Gong J,Mukherjea A.Solution of a problem on the identification of parameters by the distribution of the maximum random variable: a multivariate normal case[J].J. Theor. Probab.,1991,4(4)：783-790.

[14]Mukherjea A, Stephens R.Identification of the parameters of a trivariate normal vector by the distribution of the minimum[J].Journal of Statistical Planning and Inference,1999,78(1)：23-37.

[15]Dai M,Mukherjea A.Identification of the parameters of a multivariate normal vector by the distribution of the maximum [J].J. Theor. Probab.,2001,14：267-298.

[16]Davis J,Mukherjea A.Identification of parameters by the distribution of the minimum: The tri-variate normal case with negative correlations[J].Journal of Multivariate Analysis,2007,98(6)：1141-1159.

[17]Bi L,Mukherjea A.Identification of parameters and the distribution of the minimum of the tri-variate normal[J].Statistics & Probability Letters,2010,80(23)：1819-1826.

[18]Mukherjea A,Elnaggar M.Solution of the problem of the identified minimum for the tri-variate normal[J].Proc. Indian Acad. Sci. (Math. Sci.),2012,4(122)：645-660.

Maximum Likelihood Estimation of the Parameters of Kundu-Gupta Bivariate Bernoulli Distributions

LIGuo-an，LIJian-feng

(Department of Mathematics, Ningbo University, Ningbo 315211，China)

Abstract:Maximum likelihood estimation of the parameters of Kundu-Gupta bivariate bernoulli distributions is considered in this paper, using a way of parameters identifiability to parameter estimation, this paper shows: if two random variable have a Kundu~Gupta’s type bivariate binomial distribution, when the distribution of identified minimum is known, then all of parameters are identified; hence, the maximum likelihood estimator of all of parameters are derived.Two of them are unbiased, the mathematical expectation of another one is not exist. Monte Carlo simulations are also performed to verify the maximum likelihood estimator of all of parameters are stable to truth-value respectively.

Key words:a Kundu-Gupta’s type bivariate bernoulli distribution; identifiability; maximum likelihood estimator; unbiased; simulations

[中图分类号]O212.4

[文献标识码]A

[文章编号]1672-1454(2015)04-0113-07