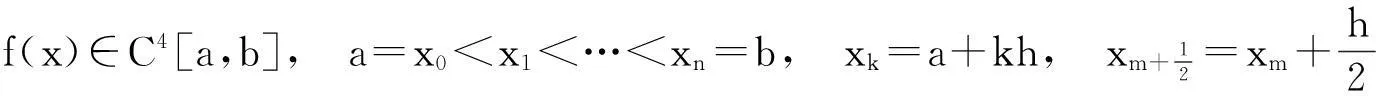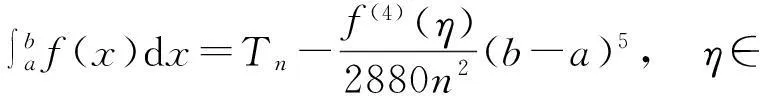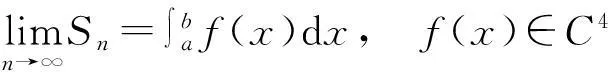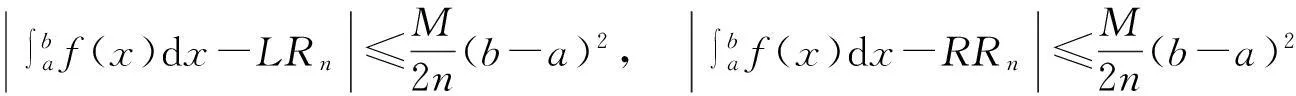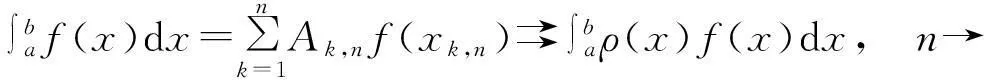关于求积公式序列收敛性的注记

钱　江，　郑苏娟，　王　凡，　吴云标

(1.河海大学理学院，南京210098；　2.南京农业大学工学院基础课部，南京210031；

3.河海大学文天学院基础部，安徽马鞍山243031)

关于求积公式序列收敛性的注记

钱江1，郑苏娟1，王凡2，吴云标3

(1.河海大学理学院，南京210098；2.南京农业大学工学院基础课部，南京210031；

3.河海大学文天学院基础部，安徽马鞍山243031)

[摘要]利用Romberg递推求积算法，证明当子区间数目趋于无穷大时，复化求积公式序列一致收敛于积分真值，证明过程与插值型求积公式序列如Gauss型求积公式序列一致收敛不同.

[关键词]一致收敛; 求积余项; 复化求积公式序列; 插值型求积公式

1引言

数学分析[1]课程中，函数列或函数项级数的“收敛性”与“一致收敛性”是初学者在学习时容易困惑的知识点. 近年来，人们对函数列或函数项级数的一致收敛性问题进行了一些研究. 葛仁福[2]结合一致连续的性质，得到了函数列一种新的一致收敛判别法. 傅湧[3]利用等度连续性, 得出了某些闭区间上连续函数列一致收敛的充要条件, 进而推广了Dini定理.刘江蓉[4]通过典型例子,从不同角度解析函数列一致收敛性的概念, 并分析其应用性质.

然而，关于函数列或函数项级数的一致收敛性与其它学科理论联系的研究值得思考，如徐业基[5]改进了平稳随机过程的采样定理，并给出了其一致收敛速度与误差估计. 这种理论应用研究开阔了人们认识一致收敛性的视野. 鉴于此，作者研究“一致收敛性”在数值分析[6]与数值逼近[7]中的作用. 主要内容包括分段低次插值序列一致收敛性问题[8]，与求积公式序列是否收敛于积分真值等. 本文主要研究后者，具体而言围绕如下两问题展开.

问题1Newton-Cotes公式序列是否收敛于积分的真值？

问题2对于f(x)∈CI复化梯形与Simpson公式序列是否都收敛于积分的真值？

2一致收敛性

定义2.1[1]设函数列{an(x)}与函数f(x), x∈D, 若∀ε>0,∃N(ε)∈N,使得当n>N时，对一切x∈D都有

|an(x)-f(x)|<ε,

则称函数列{an(x)}在D上一致收敛于f(x), 记作

根据下文需要，先回顾数值逼近[2]或数值分析[3]中一元Lagrange插值多项式理论.

定理2.1[6,7]设f(x)∈C(n+1), pn(x)为n+1个互异节点诸xi上的n次Lagrange插值多项式，则有插值余项

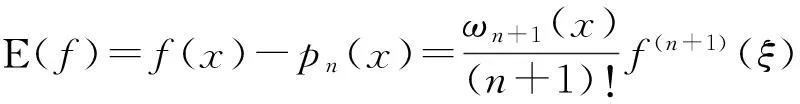
(2.1)

其中

ωn+1(x)=(x-x0)…(x-xn),ξ∈(a,b).

3插值型复化求积公式序列的收敛性

问题1Newton-Cotes公式序列是否收敛于积分的真值？

定理3.1[7]设诸互异节点xk,n∈[a,b](k=1,…,n),插值余项记为E[f],则插值型求积公式序列

代数精度至少为n-1. 若数列

定理3.2[7]令Ak,n,k=0,…,n表示n+1点Newton-Cotes公式中的系数，则

注3.1上述定理表明，Newton-Cotes公式序列并不总是收敛于积分的真值.

问题2对于f(x)∈C[a,b]，复化梯形公式与Simpson公式序列是否都收敛于积分的真值？

复化左矩形公式: 设

f(x)∈C1[a,b],a=x0

(3.1)

复化右矩形公式: 设

f(x)∈C1[a,b],a=x0

(3.2)

复化梯形公式[6,7]: 设

f(x)∈C2[a,b],a=x0

(3.3)

复化Simpson公式[6,7]: 设

k=0,1，…,n,m=0,1,…,n-1,

(3.4)

由上述求积余项序列一致收敛性易知

然而上述结论成立对函数f(x) 的光滑性条件要求颇高，更进一步，有

定理3.3设f(x)∈C1[a,b],则复化梯形与Simpson公式序列也都收敛于积分真值.

证由题设知，由于∃M>0，使得复化左矩形与右矩形公式的求积余项序列

故由函数列一致收敛的Weierstrass判别法知，求积余项序列都一致收敛于0，从而

又由于

故在题设条件下复化梯形与Simpson公式序列也都一致收敛于积分真值.

注3.2按Romberg递推求积算法得到的复化求积序列一致收敛于积分真值.

值得注意的是，随着子区间数n趋于无穷大, 能收敛于积分真值的求积公式除了上述复化求积序列，还有Gauss型求积公式，即具有2n+1次代数精度的插值型求积公式. 关于其收敛性的理论证明主要借助于Weierstrass逼近定理与其较高的代数精度性质.

定理3.4[7]设f(x)∈C[a,b].Gauss型求积公式序列

事实上，由Weierstrass逼近定理, ∀ε1>0, ∃N=N(ε1)∈使得

|f(x)-qN(x)|<ε1,x∈[a,b].

记

若n>N,由求积公式对qN(x)精确成立，则当n>N时，由Gauss型求积系数为正数，

注3.3定理3.4 证明过程表明，对于插值型求积公式，若f(x)∈C[a,b],且诸求积系数为正，则求积公式序列收敛于积分的真值. 这与按Romberg递推求积算法得到的复化求积序列一致收敛于积分真值的证明不同.

[参考文献]

[1]华东师范大学数学系. 数学分析(下册)[M].4版. 高等教学出版社, 2010.

[2]葛仁福. 函数列一致收敛判别法[J]. 大学数学, 2011, 27(4): 179-181.

[3]傅湧. 有界闭区间上连续函数列一致收敛的充要条件[J]. 大学数学, 2007, 23(3): 117-120.

[4]刘江蓉. 浅论函数列的一致收敛性[J]. 高等数学研究, 2009, 12(5): 47-48.

[5]徐业基. 关于平稳随机过程的采样定理的一致收敛速度[J]. 大学数学, 2009, 25(6): 48-51.

[6]李庆扬, 王能超, 易大义. 数值分析[M]. 5版. 北京：清华大学出版社, 2008.

[7]王仁宏. 数值逼近[M]. 北京：高等教学出版社, 1999.

[8]钱江. 分段低次插值多项式序列的一致收敛性[J]. 大学数学, 2014, 4(30): 7-11.

TheNotationonConvergenceofCubatureFormulaSequences

QIAN Jiang1,ZHENGSu-juan1,WANGFan2,WUYun-biao3

(1.CollegeofSciences,HohaiUniversity,Nanjing210098,China;

2.CollegeofEngineering,NanjingAgriculturalUniversity,Nanjing210031,China;

3.BasicResearchDepartment,HohaiUniversityWentianCollege,MaanshanAnhui243031,China)

Abstract:BymeansofRombergrecurrencecubaturealgorithm,compositecubatureformulasequencesareillustratedtoconvergetotheintegraluniformlyasthenumberofsubintervalsapproachesInfinite,theproofofwhicharedifferentfromthatofinterpolatingcubatureformulasequences,suchasGaussiantypecubatureformula.

Keywords:uniformconvergence;residualitemofcubature;compositecubatureformulasequence;interpolatingcubatureformula

[中图分类号]O171

[文献标识码]C

[文章编号]1672-1454(2015)04-0049-04