Lagrange问题与平均运动

谢建华

(西南交通大学力学与工程学院，成都610031)

Lagrange问题与平均运动

谢建华

(西南交通大学力学与工程学院，成都610031)

[摘要]介绍了天体力学中的Lagrange问题，并结合三连杆机构模型，讨论了Weyl解决这个问题的基本思想和关于平均运动的主要结论.

[关键词]天体力学； Lagrange问题； 平均运动； 遍历性； Weyl

1引言

图1　托勒密的本轮系统

在哥白尼(1473-1543)之前，人们以为地球是世界的中心，其它星体都围绕着地球旋转.托勒密为解释行星的视运动问题，提出所谓的本轮系统.根据这个系统，行星沿着一个小圆作匀速圆周运动，这个小圆称为本轮(epicycle)，本轮的圆心也沿着一个大圆的中心作匀速圆周运动，这个大圆称为均轮(deferent)(图1(a)).为描述火星的运动，托勒密加了第二个本轮，火星在第二本轮上匀速圆周运动，而第二个本轮的圆心又在第一个本轮上作匀速圆周运动(图1(b)).后来，随着观测精度的提高，为了使理论值与火星的观测数据一致，本轮的数目也一再增加，到了十八世纪，本轮的数目竟达到了22个[1].

今天，托勒密本轮系统已成为了历史，但是，与 其相关联的所谓Lagrange问题却在数学和力学发展史上占据了重要的地位.特别是Weyl[2，3]将遍历理论、概率论和复变函数方法巧妙地结合，解决了Lagrange问题，得到了平均运动的一般性结论，成为了数学和力学完美结合一个范例，值得玩味和欣赏.可惜的是Weyl的工作所牵涉的数学概念和工具较多，而且原始文献年代久远，不易获得，这给一般的读者带了很多的不便.本文结合理论力学中的三连杆机构模型，介绍了Weyl解决Lagrange问题的主要技巧和关于平均运动的主要结论.

2Lagrange问题

图2　Lagrange问题的简化模型

假设频率ω1，ω2，ω3是非共振的[4，5]，即若整数k1，k2，k3，使

k1ω1+k2ω2+k2ω3=0，

则k1=k2=k3=0.

设

φ1=ω1t+α1，φ2=ω2t+α2，φ3=ω3t+α3，

及

θ1=φ1/2π，θ2=φ2/2π，θ3=φ3/2π，θ=φ/2π.

将z表示成

(1)

另一方面z=re2πiθ，对其关于t求导，得

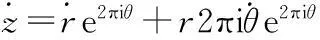
(2)

用1/(2πiz)乘(2)式两边，利用

可得

(3)

将(1)代入(3)，得

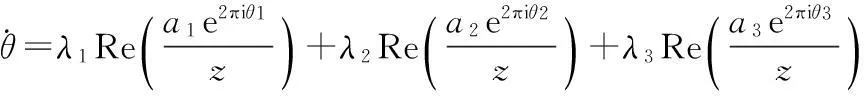
(4)

其中λi=ωi/2π(i=1，2，3).由(4)

(5)

由于(θ1，θ2，θ3)∈T3(三维环面)，而且(5)中的被积函数Re(aie2πiθi/z)在T3上是Riemann可积的，根据平均值相等定理(Kronecker-Weyl定理)[5，6]

(6)

令θ=θ3，(6)可写成

(7)

图3　复平面上的积分环路

考虑积分(7)，对取定的θ1和θ2，如果

|a1e2πiθ1+a2e2πiθ2|

(8)

(7)最里层是沿以A2为中心、半径为a3圆C上的积分，且z=0在此圆的内部(图3(a))，故

(9)

如果|a1e2πiθ1+a2e2πiθ2|>a3，则z=0在圆C的外部(图3(b))，积分(9)为0.

如果取定θ2和θ3，而让θ=θ1变化，或取定θ1和θ3，而让θ=θ2变化，关于W1和W2的积分也有相同的结果(图3(c)，(d)).

如果用P(|a1e2πiθ1+a2e2πiθ2|

W3=P(|a1e2πiθ1+a2e2πiθ2|

(10)

同理

W1=P(|a2e2πiθ2+a3e2πiθ3|

(11)

于是，由(5)，得

(12)

(13)

如果ω1=ω2=ω3=ω0，显然ω=ω0，由(13)可得

W1+W2+W3=1.

(14)

例假设a1>a2+a3，那么对任何(θ1，θ2，θ3)∈T3，有

|a2e2πiθ2+a3e2πiθ3|

于是W1=1，从而W2=W3=0，由(13)，ω=ω1.

上例中的特殊情况称为Lagrange情形，对三杆能构成一个三角形的非Lagrange情形，Bohr给出一般的解答：πWi是三角形边ai对应角的角度[2，5].

3结论语

Lagrange问题起源于关于太阳系的稳定性研究：由于太阳系中各行星的轨道几乎在同一个平面内，并近似为圆形轨道，Lagrange考虑了连接太阳和行星的向量(Laplace向量)，在摄动一次近似理论之下，Laplace向量受行星相互引力作用的影响，其运动如同匀速旋转的向量.Lagrange计算了太阳系中各行星的频率ωk和振幅ak，除地球和金星以外(非Lagrange情形)，计算出了其余各行星近日点的平均运动[5].研究表明行星轨道的离心率在原点附近作很小的周期性振荡，因此太阳系是稳定的；地球轨道离心率的振荡周期性是与地球上冰期的变化规律密切相关的[5]；另外，关于Lagrange问题和平均运动的研究也促进了拟周期函数和遍历理论的发展[6]；在对Lagrange问题研究中还发现了一些十分有趣的流形的拓扑学问题[2]，因此Lagrange问题研究的理论和应用意义都是很大的.

[参考文献]

[1]刘步林.数学在天文学中的运用[M].北京:科学出版社，1979.

[2]Weyl H. Mean motion[J]. Amer. J. of Math.， 1938，60:889-896.

[3]Weyl H. Mean motion(II)[J]. Amer. J. of Math.， 1939，61:143-148.

[4]Sternberg S . Celestial Mechanics[M]. New York:W.A.Benjamin，Inc.，1969.

[5]阿诺尔德B N.常微分方程续论—常微分方程的几何理论[M]. 齐民友译.北京:科学出版社，1989.

[6]Arnold V I， Avez A. Ergodic Problems of Classical Mechanics[M]. New York:W.A.Benjamin，Inc.，1968.

Lagrangian Problem and Mean Motion

XIEJian-hua

(School of Mechanics and Engineering， Southwest Jiaotong University，Chengdu 610031，China)

Abstract:This paper has introduced the Lagrangian problem in celestial mechanics ， and by using the three bar’s model ， we discussed Weyl’s idea to solve this problem and his key results for mean motion.

Key words:celestial mechanics; Lagrangian problem; mean motion; ergodicity; Weyl

[中图分类号]O312.2

[文献标识码]A

[文章编号]1672-1454(2015)04-0123-04