CN环的若干等价刻划

潘　勇，　魏俊潮

(1.扬州职业大学数学科学学院，江苏扬州225009；　2.扬州大学数学科学学院，江苏扬州225002)

CN环的若干等价刻划

潘勇1，魏俊潮2

(1.扬州职业大学数学科学学院，江苏扬州225009；2.扬州大学数学科学学院，江苏扬州225002)

[摘要]引入环的补左零化子集的概念，给出了CN环几个新的等价刻划.

[关键词]CN环； 幂零元； 补左零化子集

1引言

如果环R的每个幂零元素均为中心元,则称R为CN环[1].显然,交换环和约化环(即R没有非零的幂零元素)都是CN环.文献[2]中给出了CN环几个等价刻划：

(i)R为CN环当且仅当对任意a∈N(R)，存在整数n=n(a)≥2使得a-an∈Z(R)；

(ii)R为CN环当且仅当对任意的x∈N(R),y∈R，有

((1+x)y)n+k=(1+x)n+kyn+k，k=0,1,2；

(iii)R为CN环当且仅当对任意的x∈N(R),y∈R，有

((1+x)y)n+k=yn+k(1+x)n+k，k=0,1,2.

本文引入补左零化子集的概念，对文献[2]给出的CN环几个等价刻划作了改进，给出了条件更一般的等价刻划.

2基础知识

本文中R表示有单位元的结合环.N(R)，Z(R)，J(R)，Zr(R)，Zl(R)分别表示环R的幂零元集合、中心、Jacobson根和左、右奇异理想；Z[x]表示整系数多项式环；l(a),r(a)分别表示a在环R中的左、右零化子；相关概念参见[3].

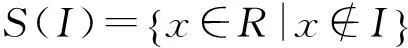
首先给出几个引理：

引理2.1设R是一个环，f(x)∈Z[x]，且f(x)常数项为零，则对任意的a∈N(R)，有

f(a)∈N(R)，且af(a)=f(a)a.

引理2.2[4]设R是一个环，对任意的x∈R，若l(x)=0,则

l(x2)=l(x3)=…=l(xn),

其中n为正整数.

引理2.3[5]设R是一个环，n为正整数，x,y∈R, 若xyn=0=x(1+y)n，则x=0.

3主要结论

先给出[2，定理2.1]一个推广：

定理3.1R为CN环当且仅当对任意a∈N(R)，存在整数n=n(a)≥2，使得

a-(f(a))n∈Z(R)，

其中f(x)∈Z[x]，且f(x)常数项为零.

证显然.

⟸设f(x)∈Z[x]，且f(x)常数项为零.不妨设f(x)=xf0(x)，且f0(x)∈Z[x].

任取a∈N(R)，存在m>0,使得am=0.由题设可知：存在n1=n(a)≥2，使得

a-(f(a))n1∈Z(R)，

由引理2.1可知

(f(a))n1=an1(f0(a))n1∈N(R),

则有

(f(a))n1=an1a1∈N(R)，

其中a1=(f0(a))n1，且an1a1=a1an1.

同样由题设可知：存在n2=n(an1a1)≥2，使得

an1a1-(f(an1a1))n2∈Z(R),

由引理2.1可知

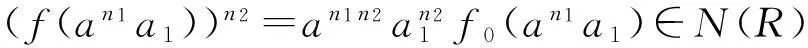
则有

(f(an1a1))n2=an1n2a2∈N(R)，

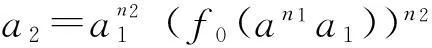
以此类推，存在ns=n(an1n2…ns-1as-1)≥2，使得

an1n2…ns-1as-1-(f(an1n2…ns-1a1))ns∈Z(R)，

且

n1n2…ns>m，(f(an1n2…ns-1a1))ns=an1n2…nsas=0，

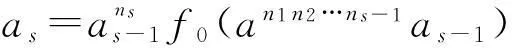
利用补左零化子集，下面给出[2，定理2.4]的推广：

定理3.2设R是一个环，I是R的补左零化子集，则下列条件等价：

(i)R为CN环.

(ii) 对任意的x∈N(R),y∈RI，有

((1+x)y)n+k=(1+x)n+kyn+k,k=0,1,2,n为某一确定的正整数.

(iii) 对任意的x∈N(R),y∈RI，有

((1+x)y)n+k=yn+k(1+x)n+k,k=0,1,2,n为某一确定的正整数.

(iv) 对任意的x∈N(R),y∈RI，有

((1+x)y)n+k=yk(1+x)n+kyn,k=0,1,n为某一确定的正整数.

证(i)(ii),(iii),(iv)显然.

((1+x)(1-y))n+k=(1+x)n+k(1-y)n+k,k=0,1,2,

则有

((1+x)(1-y))n+1=(1+x)n+1(1-y)n+1,

((1+x)(1-y))n+1=(1+x)(1-y)(1+x)n(1-y)n,

所以

(1+x)n+1(1-y)n+1=(1+x)(1-y)(1+x)n(1-y)n.

即有

(1+x)(y(1+x)n-(1+x)ny)(1-y)n=0.

由x∈N(R)，可知1+x可逆；l(1-y)=0，由引理2.2可知

l((1-y)n)=0,

所以，有

y(1+x)n=(1+x)ny.

(1)

同理有

y(1+x)n+1=(1+x)n+1y.

(2)

(1)右乘1+x，减(2)得

(1+x)n(yx-xy)=0,

从而

yx-xy=0.

若y∉I即y∈RI，由已知条件有

((1+x)y)n+k=(1+x)n+kyn+k,k=0,1,2,

则有

((1+x)y)n+1=(1+x)n+1yn+1,

((1+x)y)n+1=(1+x)nyn(1+x)y,

所以

(1+x)n+1yn+1=(1+x)nyn(1+x)y.

即有

(1+x)n(xyn+1-ynxy)=0.

由x∈N(R)，可知1+x可逆，可得

xyn+1-ynxy=0.

即

xyn+1=ynxy.

(3)

同理有

xyn+2=yn+1xy.

(4)

(3)左乘y，减(4)得

(yx-xy)yn+1=0,

(5)

若1+y∉I，即1+y∈RI，用1+y替代(5)的y可得

(yx-xy)(1+y)n+1=0.

(6)

由引理2.3及(5),(6)可得

yx-xy=0,

若1+y∈I，则1-(1+y)=-y∉I且l(-y)=0，从而l(y)=0，由引理2.2可知l(yn+1)=0.由(5)可得

yx-xy=0.

综上所述，对任意的x∈N(R),y∈R，都有

yx-xy=0

成立，所以R为CN环.

由已知条件有

((1+x)(1-y))n+k=(1-y)n+k(1+x)n+k,k=0,1,2,

则有

((1+x)(1-y))n+1=(1-y)n+1(1+x)n+1,

((1+x)(1-y))n+1=(1+x)(1-y)n+1(1+x)n,

所以

(1-y)n+1(1+x)n+1=(1+x)(1+y)n+1(1+x)n.

即有

((1-y)n+1x-x(1-y)n+1)(1+x)n=0.

由x∈N(R)，可知1+x可逆，可得

(1-y)n+1x-x(1-y)n+1=0.

即

(1-y)n+1x=x(1-y)n+1.

(7)

同理有

(1-y)n+2x=x(1-y)n+2.

(8)

(7)左乘1-y，减(8)得

(xy-yx)(1-y)n+1=0.

因为l(1-y)=0，由引理2.2可知l(1-y)n+1=0.从而，有

xy-yx=0.

若y∉I即y∈RI，由已知条件有

((1+x)y)n+k=yn+k(1+x)n+k,k=0,1,2,

则有

((1+x)y)n+1=yn+1(1+x)n+1,

((1+x)y)n+1=(1+x)yn+1(1+x)n,

所以

yn+1(1+x)n+1=(1+x)yn+1(1+x)n.

即有

(yn+1x-xyn+1)(1+x)n=0.

由x∈N(R)，可知1+x可逆，可得

yn+1x-xyn+1=0.

即

yn+1x=xyn+1.

(9)

同理有

yn+2x=xyn+2.

(10)

(9)左乘y，减(10)可得

(yx-xy)yn+1=0,

(11)

若1+y∉I，即1+y∈RI，用1+y替代(11)的y可得

(yx-xy)(1+y)n+1=0.

(12)

由引理2.3及(11),(12)可得

yx-xy=0.

若1+y∈I，则1-(1+y)=-y∉I且l(-y)=0，从而l(y)=0，由引理2.2可知l(yn+1)=0,由(11)可得

yx-xy=0.

综上所述，对任意的x∈N(R),y∈R，都有yx-xy=0成立，所以R为CN环.

((1+x)(1-y))n+k=(1-y)k(1+x)n+k(1-y)n,k=0,1,

则有

((1+x)(1-y))n+1=(1-y)(1+x)n+1(1-y)n,

((1+x)(1-y))n+1=(1+x)(1-y)(1+x)n(1-y)n,

所以

(1-y)(1+x)n+1(1-y)n=(1+x)(1-y)(1+x)n(1-y)n.

即

(xy-yx)(1+x)n(1-y)n=0.

因为l(1-y)=0，由引理2.2可知l(1-y)n=0.可得

(xy-yx)(1+x)n=0.

由x∈N(R)，可知1+x可逆，可得

xy-yx=0.

若y∉I即y∈RI，由已知条件有

((1+x)y)n+k=yk(1+x)n+kyn,k=0,1,

则

((1+x)y)n+1=y(1+x)n+1yn,

((1+x)y)n+1=(1+x)y(1+x)nyn,

所以

y(1+x)n+1yn=(1+x)y(1+x)nyn.

即

(yx-xy)(1+x)nyn=0.

(13)

若1+y∉I，即1+y∈RI，用1+y替代(13)的y可得

(yx-xy)(1+x)n(1+y)n=0.

(14)

由引理2.3及(13),(14)可得

(yx-xy)(1+x)n=0.

若1+y∈I，则1-(1+y)=-y∉I且l(-y)=0，从而l(y)=0，由引理2.2可知l(yn)=0,由(13)得

(yx-xy)(1+x)n=0.

无论1+y∉I，或1+y∈I，总有

(yx-xy)(1+x)n=0.

由x∈N(R)，可知1+x可逆，可得

yx-xy=0.

综上所述，对任意的x∈N(R),y∈R，都有

yx-xy=0

成立，所以R为CN环.

[参考文献]

[1]Drazin M P. Rings with central idempotent or nilpotent elements [J] . Proc Edinburgh Math Soc, 1958, 9(2) : 157-165.

[2]Wei Junchao.Some notes onCNrings [J].bull Malays Math Sci Sco，2014，37(3): 25-37.

[3]Anderson F W,Fuller K R.Rings and categories of modules[M].2nded.New York:Springer-Verlag, 1992.

[4]杜巧利，孙建华.环的右奇异理想与交换性定理[J].扬州大学学报(自然科学版)，2014，17(4)：5—7.

[5]Nicholson W K and Yaqub A. A commutativity theorem[J]. Algebra Universalis, 1980，10:260-263；113-116.

Several Equivalent Characterizations of CN Rings

PANYong1,WEIJun-chao2

(1. School of Mathematical Sciences，Yangzhou Polytechnic College ,Yang zhou Jiangsu 225009 ,China;

2. School of Mathematical Sciences, Yangzhou University ,Yangzhou Jiangsu 225002,China)

Abstract:The complementary left annihilator of rings is introduced, and some new equivalent characterizations ofCNrings are given.

Key words:CNring；nilpotent element；complementary left annihilator

[中图分类号]O153.3;O154

[文献标识码]A

[文章编号]1672-1454(2015)04-0099-06