广义浅水波方程新的行波解

王　鑫,　邢文雅,　李胜军

(海南大学信息科学技术学院, 海口570228)

广义浅水波方程新的行波解

王鑫,邢文雅,李胜军

(海南大学信息科学技术学院, 海口570228)

[摘要]通过利用新的G展开法，并借助Mathematica计算软件，研究了广义浅水波方程的精确解，获得了该方程的含有多个任意参数的新的显式行波解，分别为三角函数解、双曲函数解、有理函数解和指数函数解，扩大了该类方程的解的范围.

[关键词]广义浅水波方程； 新的G展开法； 行波解

1引言

本文研究广义浅水波方程[1-2]

uxxxt+αuxuxt+βutuxx-uxt-uxx=0，

(1)

其中α,β为任意非零常数且α+β≠0.此方程是在经典浅水波理论中用Boussinesq逼近法得到的，它常用于描述浅水波在(1+1)维空间中的运动规律.Clarkson and Mansfield在文献[2]得到了该方程的完全可积的充分必要条件是α=β或α=2β，且用反散射法验证了此时的可解性；文献[3]证明了当α=β或α=2β时，此方程能表示成Hirota’s的双线性形式；文献[4]运用Backlund变换的变量分离法求出了该方程的含有低维任意函数的变量分离解.

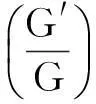
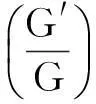
2新的G展开法

对于非线性偏微分方程

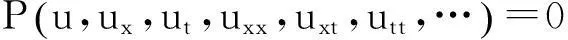
(2)

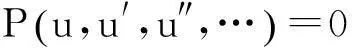
(3)

设方程(3)的解有如下形式

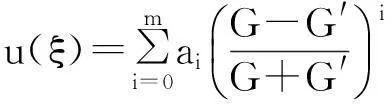
(4)

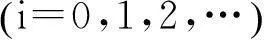
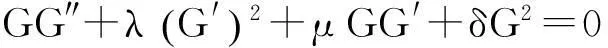
(5)

这里λ，μ及δ为任意常数.对于此方程，通过借助Mathematica软件，可求得其以下几种解的情况，

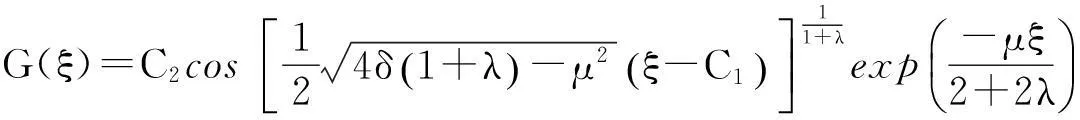
(6)

这里C1，C2为积分常数.

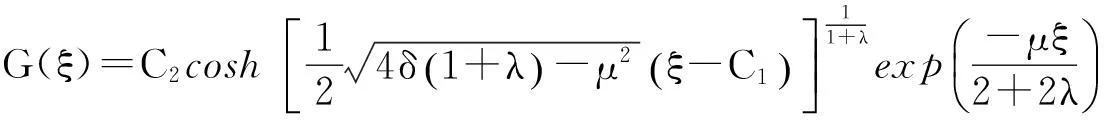
(7)

这里C1，C2为积分常数.

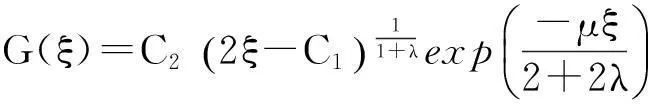
(8)

这里C1，C2为积分常数.

④ 当λ=-1且μ≠0时，方程(5)的解为

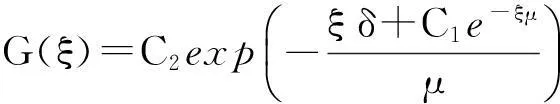
(9)

这里C1，C2为积分常数.

⑤ 当λ=-1且μ=0时，方程(5)的解为

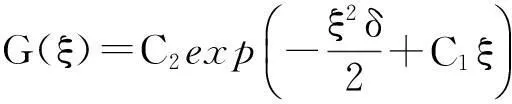
(10)

这里C1，C2为积分常数.

3广义浅水波方程新的行波解

设方程(1)有行波解

u=u(ξ)=u(x-ct)，

其中c表示波速，是一非零常数，从而方程可化为

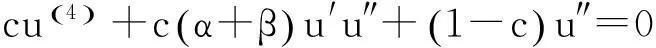
将方程两边关于ξ积分并化简，得

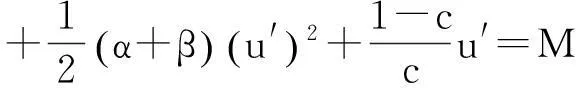
(11)

其中M为任意常数.设广义浅水波方程(1)的解能够表示成多项式

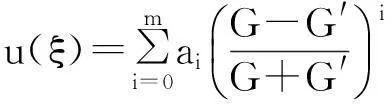
且G=G(ξ)满足二阶非线性常微分方程

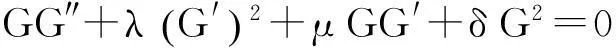
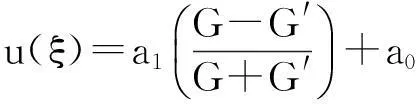
(12)

由方程(5)式和(12)式可得

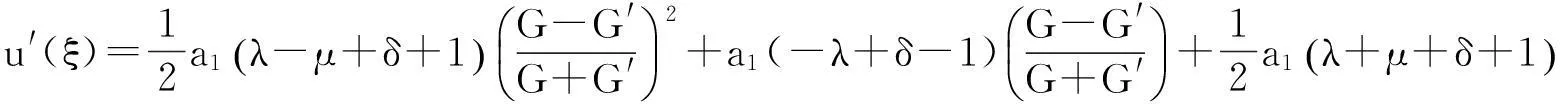
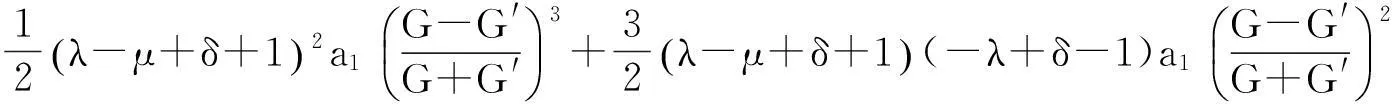
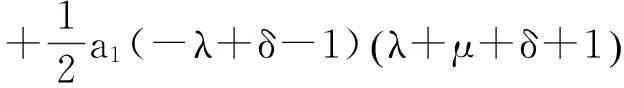
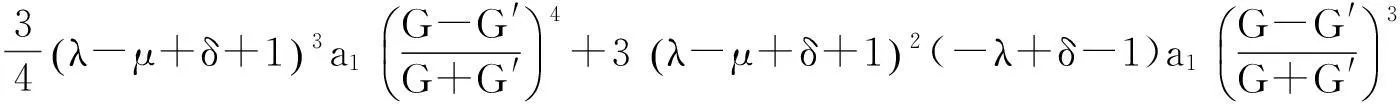
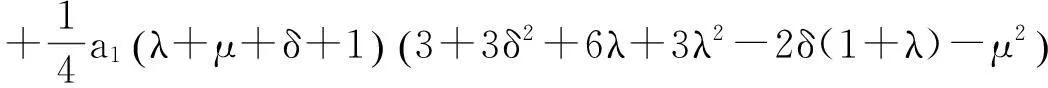
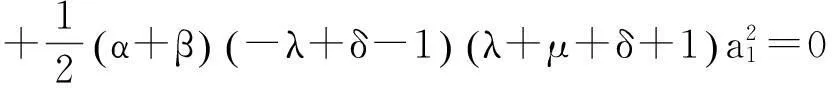
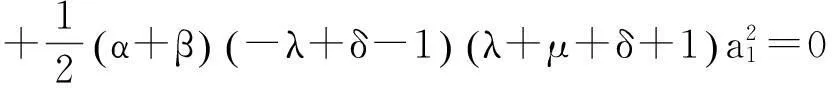
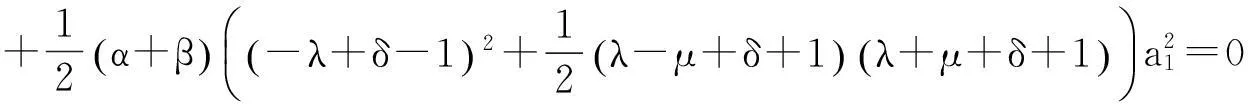
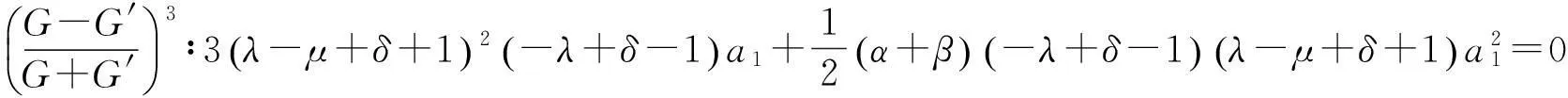
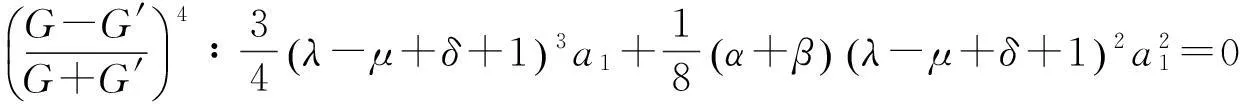
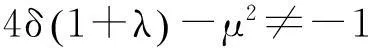
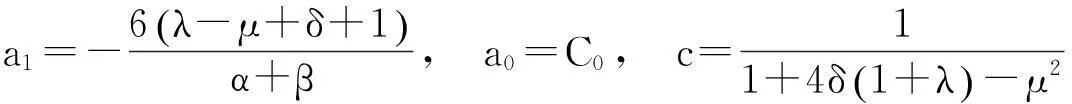
(13)

其中C0为任意常数，将(13)式代入(12)式，得到

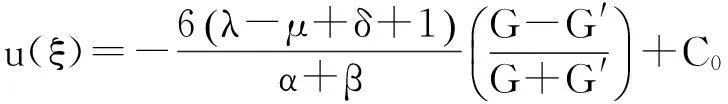
由于G满足方程(5)式，从而我们可以得到下列广义浅水波方程的显式行波解：

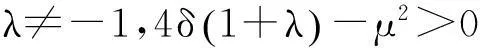
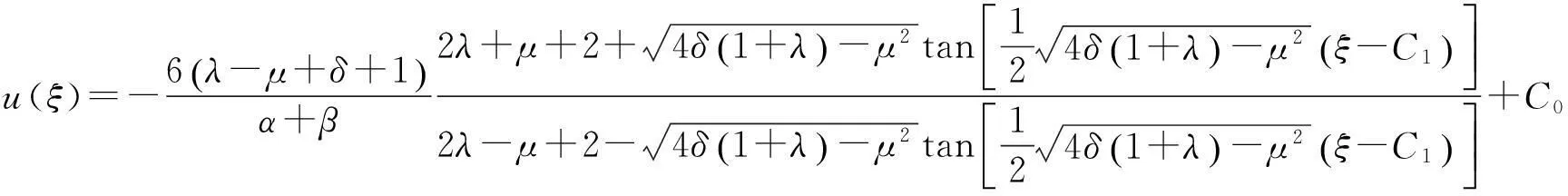
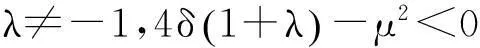
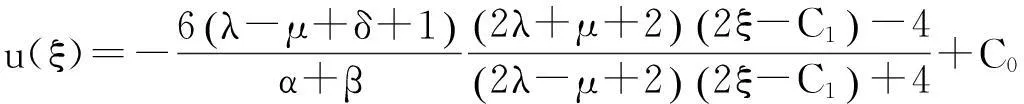
这里ξ=x-t.此为方程(1)的有理函数形式的解.

④ 当λ=-1，μ≠0且μ≠±1时，由(9)式，可得方程(1)的解为

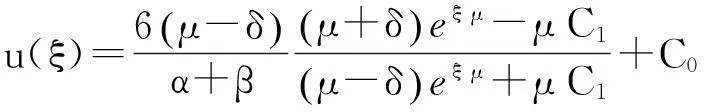
⑤ 当λ=-1，μ=0时，由(10)式，可得方程(1)的解为

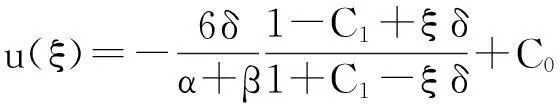
这里ξ=x-t.此为方程(1)的另一有理函数形式的解.

4结论

[参考文献]

[1]Whitham G B. Linear and Nonlinear Waves[M]. New York: Wiley-Interscience, 1974.

[2]Clarkson P A. Mansfield E L. On a shallow water wave equation[J]. Nonlinearity, 1994, 7: 975.

[3]Hietarinta J, Conte R, Boccara N. Editors NATO ASI Seres C: Mathematical and Physical Sciences[M]. Dordrecht: Kluwer, 1990，310： 459-478.

[4]沈守枫. (1+1)维广义的浅水波方程的变量分离解和孤子激发模式[J]. 物理学报, 2006, 55(3):1016-1022.

[5]Wang M L, Li X Z, Zhang J L. The (G’/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics [J]. Phys. Lett. A, 2008, 372: 417-423.

[6]Wang M L, Zhang J L, Li X Z. Application of the (G’/G)-expansion to travelling wave solutions of the Broer-Kaup and the approximate long water wave equations [J]. Appl Math Comput, 2008, 206: 321-326.

[7]Li L X, Wang M L. The (G′/G)-expansion method and travelling wave solutions for a higher-order nonlinear schrodinger equation [J]. Appl Math Comput, 2009, 208: 440-445.

[8]Wang M L. Solitary wave solution for variant Boussineq equations [J]. Phys. Lett. A, 1995, 199: 169-172.

[9]Wang M L. Exact solutions for a compound Kdv-Burgers equation [J]. Phys. Lett. A, 1996, 213: 279-287.

[10]Wang M L, ect. Application of homogeneous balance method to exact solutions of nonlinear evolution equation in mathematical physics [J]. Phys. Lett. A, 1996, 216: 67-73.

[11]薛丰刚, 丁丹平. 二阶Camassa-Holm 方程行波解[J]. 大学数学, 2013, 29(6):30-34.

[12]王艳红, 刘新乐，姬鹏斌. 广义KdV方程与广义Burgers方程的精确解[J]. 大学数学, 2012, 28(16):111-113.

[13]曹瑞.G′/G方法构造(2+1)维破裂孤子方程的精确解[J]. 大学数学, 2012, 28(2):34-36.

New Travelling Wave Solutions for the Generalized Shallow Water Wave Equation

WANGXin,XINGWen-ya，LISheng-jun

(College of Information Science and Technology, Hainan University, Haikou 570228, China)

Abstract:The generalized shallow water wave equation is studied by the new G-expansion method with the aid of computer symbolic systems Mathematica. As a result, some new explicit travelling wave solutions which involving parameters are obtained, these solutions contain the hyperbolic function solutions, the trigonometric function solutions, the rational function solutions and the exponential function solutions. The solutions of the generalized shallow water wave equation have been enriched.

Key words:generalized shallow water wave equation; new G-expansion method; travelling wave solutions

[中图分类号]O175.29

[文献标识码]A

[文章编号]1672-1454(2015)04-0009-05