线性流形的性质

张建刚，　申　冉

(1.上海师范大学数学系，上海200234;　2.东华大学理学院，上海201620)

线性流形的性质

张建刚1，申冉2

(1.上海师范大学数学系，上海200234;2.东华大学理学院，上海201620)

[摘要]线性流形作为n维数组向量空间的子集合， 与线性方程组的解和n维数组向量空间的子空间有着密切的联系.通过讨论线性流形的一些基本性质，研究其与线性方程组的解，线性子空间的关系，从而加深对这一概念的理解.

[关键词]线性流形； 线性方程组； 子空间

1引言

线性方程组是线性代数的一个核心内容.众所周知，齐次线性方程组AmnX=0的解是n维数组向量空间的一个线性子空间.而非齐次线性方程组AmnX=b(≠0)的解集合不是一个子空间，是n维数组向量空间的一个线性流形.对于线性流形的研究，可以帮助我们进一步了解线性方程组解的结构.

在本文中，首先给出n维数组空间的线性流形一个整体刻画.然后研究线性流形和线性子空间的关系，线性流形之间的运算，以及它们和相应的线性方程组的解的关系.上述工作，有助于我们理解方程组解的结构和性质，同时，加深对于线性流形的理解和认知.

文中所有术语，可参见文献[1]和[2].

2线性流形的性质

定义2.1[1]设V是数域K上n维数组向量空间(以下简称n维数组空间)，Y是向量空间V的非空子集. 对任意的α,β∈Y，若

L={kα+lβ|k+l=1,k,l∈K}⊆Y，

则称Y是向量空间V的一个线性流形.

n维数组空间V的线性子空间显然是V上的线性流形，{0}和V称为平凡的线性流形，若线性流形Y不等于{0}和V，称为非平凡的线性流形.

定理2.2设V是数域K上n维数组空间，Y⊆V，则下列情形等价：

(i) Y是向量空间V的一个线性流形.

(ii) 存在V中唯一一个线性子空间W，使得

Y=α0+W={α0+η|η∈W}，

其中α0是Y中任意取定的元素，并设dimW=r.

(iii) Y是某一线性方程组AX=b的解集合，其中A是(n-r)×n阶矩阵，且rankA=n-r.

(iv) 存在α0,α1,…,αr∈Y，使得

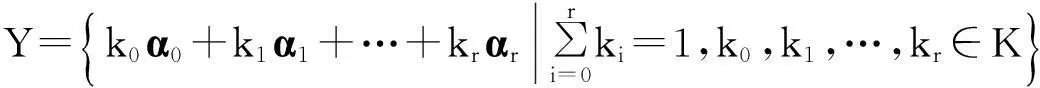
证(i)(ii). 任取α0∈Y，令W={α-α0|α∈Y}，只需证明W是V的一个子空间.首先，0=α0-α0∈W≠∅.设α1-α0,α2-α0∈W，由线性流形的定义不难看到，，且

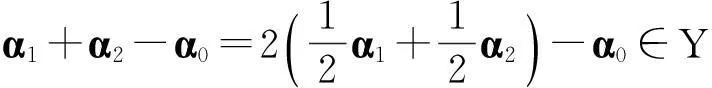
所以有

(α1-α0)+(α2-α0)=(α1+α2-α0)-α0∈W.

另一方面，对任意的α-α0∈W和k∈K，kα+(1-k)α0∈Y，且

k(α-α0)=(kα+(1-k)α0)-α0∈W，

故W是V的一个子空间，且Y=α0+W.

再证W的唯一性，假设存在另外一个线性子空间W1，使得Y=α1+W1，其中α1∈Y.则α0∈α1+W1，从而存在β∈W1，使得α0=α1+β.进一步，对任意的γ∈W，

α0+γ=α1+β+γ∈α1+W1，

即β+γ∈W1.因为W1是线性子空间，所以γ∈W1，从而W⊆W1.反包含同理可以证明，所以W=W1.

(ii)(iii). 设W的一组基为

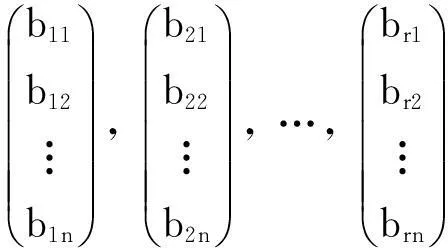
(Ⅰ)

以上述列向量组构造齐次线性方程组

(1)

容易知道该方程组是有解的，且基础解系中向量个数为n-r.不妨假设

(Ⅱ)

为方程组(1)的基础解系.再以列向量组(Ⅱ)构造齐次线性方程组

(2)

容易看到向量组(Ⅰ)就是方程组(2)的一个基础解系.令

则rankA=n-r，且W是齐次线性方程组AX=0的解空间.进一步，若Aα0=b，则易知方程组AX=b的解集合为Y=α0+W.

(iii)(iv). 设Y是线性方程组AX=b的解集合，其中A是(n-r)×n阶矩阵，且rankA=n-r.若b=0，即方程组为齐次线性方程组.设α1,α2,…,αr是该方程组的基础解系，对任意的α∈Y，存在k1,k2,…,kr∈K，使得

α=k1α1+k2α2+…krαr，

进一步，令α0=0，

α=(1-k1-k2-…-kr)α0+k1α1+k2α2+…krαr，

令k0=1-k1-k2-…-kr，则在此种情形下，结论成立.

若b≠0，即方程组AX=b为非齐次线性方程组.令γ0是方程组的一个特解，η1,η2,…,ηr是相应的导出组AX=0的基础解系.显然有γ0,γ0+η1,γ0+η2,…,γ0+ηr∈Y，下证γ0,γ0+η1,γ0+η2,…,γ0+ηr线性无关. 首先，注意到γ0,η1,η2,…,ηr线性无关.事实上，若存在k0,k1,k2,…,kr∈K，使得

k0γ0+k1η1+k2η2+…+krηr=0，

则

0=A0=k0Aγ0+k1Aη1+k2Aη2+…+krAηr=k0b.

由于b≠0，所以k0=0.进一步，由于η1,η2,…,ηr线性无关，所以

k1=k2=…=kr=0.

设

l0γ0+l1(γ0+η1)+l2(γ0+η2)+…+lr(γ0+ηr)=0，

即得到

(l0+l1+…+lr)γ0+l1η1+l2η2+…+lrηr=0，

由前面的事实可以得到，li=0,i=0,1,…r.所以γ0,γ0+η1,γ0+η2,…,γ0+ηr线性无关.

设γ是非齐次线性方程组AX=b的任一解，则γ-γ0是它的导出组AX=0的解，所以存在k1,k2,…,kr∈K，使得

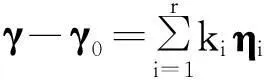
即

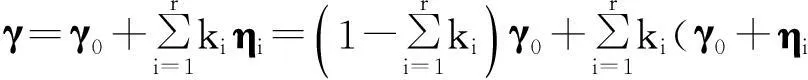
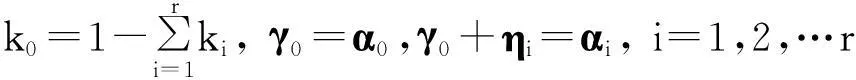
(iv)(i). 任意的α,β∈Y，不妨假设

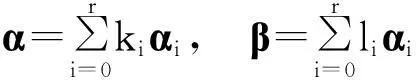
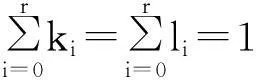
γ=k(k0α0+k1α1+…+krαr)+l(l0α0+l1α1+…+lrαr)

=(kk0+ll0)α0+(kk1+ll1)α1+…+(kkr+llr)αr.

而其中系数

(kk0+ll0)+(kk1+ll1)+…+(kkr+llr)

=k(k0+k1+…+kr)+l(l0+l1+…+lr)=k+l=1.

从而γ∈Y，所以Y是一个线性流形.

下面讨论线性流形和向量空间V的线性子空间的关系.

定理2.3设Y(=α0+W)是一个线性流形，则下列命题等价：

(i) Y不是一个线性子空间.

(ii) 0∉Y.

(iii) Y∩W=∅.

(iv) 对任意的α,β∈Y，α+β∉Y.

证(i)(ii). 若0∈Y，则Y=0+W=W是一个线性子空间，矛盾，故0∉Y.

(ii)(iii). 若Y∩W≠∅，即存在元素α∈Y∩W，由线性流形的定义可知，Y=α+W， 从而α+(-α)=0∈Y，矛盾，故Y∩W=∅.

(iii)(iv). 设α,β∈Y，不妨假设α=α0+α1,β=α0+α2,α1,α2∈W.若α+β∈Y，则存在α3∈W，使得

α+β=(α0+α1)+(α0+α2)=2α0+(α1+α2)=α0+α3，

所以α0=α3-(α1+α2)∈W，这与Y∩W=∅矛盾.

(iv)(i). 为显然.

推论2.4设Y(=α0+W)是一个线性流形，则Y是一个线性子空间当且仅当0∈Y，当且仅当Y∩W=W.

推论2.5设Y(=α0+W)是一个线性流形，则Y∩W=∅或者Y∩W=W.

命题2.6设Y1=α1+W,Y2=α2+W分别是两个线性流形，则Y1∩Y2=∅当且仅当α1-α2∉W.

证由定理2.2的证明可知，Y1,Y2可以分别看做线性方程组AX=b1和AX=b2的解集合，且共同导出组AX=0的解空间为W. 若Y1∩Y2=∅，即AX=b1和AX=b2没有公共解，则必有α1-α2∉W，否则α1-α2是导出组的解，令α1-α2=α0∈W，则α1=α0+α2，必有α1也是方程组AX=b2的解，矛盾.反之，若α1-α2∉W，则必有Y1∩Y2=∅.否则，AX=b1和AX=b2有公共解α，则b1=b2，从而Y1=Y2，α1-α2∈W，矛盾.

推论2.7设Y1=α1+W,Y2=α2+W分别是两个线性流形，则Y1∩Y2=∅或者Y1=Y2.

引理2.8[1]两个真子空间的并不可能是整个向量空间.

命题2.9两个非平凡的线性流形的并不可能是整个向量空间V.

证设Y1,Y2是V的两个线性流形，且满足{0}⊂Yi⊂V,i=1,2.若Y1,Y2均为V的真子空间，由引理2.8，Y1,Y2的并不可能为V.下面考察Y1,Y2不同时为子空间的情形，由定理2.3，也即0∉Y1∩Y2.若V=Y1∪Y2，则0∈Y1,0∈Y2必有且仅有一个成立，不妨假设0∈Y1，即Y1是V的一个真子空间，Y2不是子空间.取α∈Y2,α∉Y1，且视Y2为某一线性方程组AX=b的解空间.由于0∉Y2，故b≠0.另一方面，由定理2.3，α+α=2α∉Y2，则2α∈Y1.因为Y1是V的一个真子空间，所以α∈Y1，与前提矛盾.故V的两个非平凡的线性流形的并不可能是整个向量空间.

推论2.10设Y是一个线性流形，则VY不是一个线性流形.

设Y1,Y2是V的两个线性流形，定义

Y1+Y2={α1+α2|α1∈Y1,α2∈Y2}，

称为两个线性流形Y1,Y2的和.

命题2.11设Y1=α1+W1,Y2=α2+W2分别是两个线性流形， 则Y1∩Y2,Y1+Y2也是线性流形.

证由定理2.2，分别视Y1,Y2为线性方程组A1X=b1,A2X=b2的解集合，则Y1∩Y2是线性方程组

的解集合，从而也是一个线性流形.又

Y1+Y2=α1+W1+α2+W2=α1+α2+W1+W2，

因为W1+W2也是一个线性子空间，故Y1+Y2也是一个线性流形.

定义2.12设Y=α0+W是一个线性流形，若dimW=r，称r为线性流形Y的维数, 记作dimY=r.

命题 2.13设Y1=α1+W1,Y2=α2+W2分别是两个线性流形，则

dim(Y1+Y2)=dimY1+dimY2-dim(Y1∩Y2).

证根据线性流形维数的定义显然有

dimY1=dimW1,dimY2=dimW2，dim(Y1+Y2)=dim(W1+W2).

假设Y1,Y2分别为线性方程组A1X=b1,A2X=b2的解集合，由定理2.2，W1,W2分别为相应的导出组A1X=0,A2X=0的解空间.另一方面，Y1∩Y2是线性方程组

的解集合，并假设Y1∩Y2=α0+W0，则W0是方程组

的基础解系，显然有W0=W1∩W2，所以dim(Y1∩Y2)=dim(W1∩W2).由向量空间的维数公式易知

dim(Y1+Y2)=dimY1+dimY2-dim(Y1∩Y2).

注2.14设Y1=α1+W1,Y2=α2+W2分别是两个线性流形，分别为线性方程组A1X=b1,A2X=b2的解集合. 因为Y1+Y2=α1+α2+W1+W2也是线性流形，故它也是某个线性方程组的解集合.由定理2.2的证明不难看到，Y1+Y2可以看作线性方程组AX=b的解集合，其中系数矩阵A的行向量为方程组WX=0的基础解系，而W1+W2的一组基恰为W的行向量，且A(α1+α2)=b.

注2.15线性流形的并一般不是线性流形.在V中任取两个向量α,β，二者不成比例.令Y1=L(α),Y2=L(β)，则Y1,Y2是两个线性子空间，而(0∈)Y1∪Y2显然不是一个子空间，由推论2.4，Y1∪Y2不是一个线性流形.

[参考文献]

[1]陈志杰. 高等代数与解析几何(上)[M]. 北京：高等教育出版社，2000.

[2]易忠. 高等代数与解析几何(上)[M]. 北京：清华大学出版社，2007.

[3]彭刚，翟莹. 线性流形及其有关性质[J]. 湖北第二师范学院学报，2008, 25(8): 15-16.

PropertiesofLinearManifolds

ZHANG Jian-gang1，SHEN Ran2

(1.DepartmentofMathematics,ShanghaiNormalUniversity，Shanghai200234,China;

2.CollegeofScience，DonghuaUniversity,Shanghai201620,China)

Abstract:Alinearmanifoldisasubsetofan-dimensionalvectorspace.Ithasclosecontactwiththesolutionsofsystemsoflinearequations,andthesubspacesofn-dimensionalvectorspace.Bysomepropertiesoflinearmanifoldsgiveninthispaper,theauthorsgettherelationsoflinearmanifolds,thesolutionsofsystemsoflinearequations,andthesubspacesofn-dimensionalvectorspace,thenwehaveabetterunderstandoflinearmanifolds.

Keywords:linearmanifold；systemoflinearequations；subspace

[中图分类号]O151.2

[文献标识码]A

[文章编号]1672-1454(2015)04-0090-05