基于道路状况的冷链物流配送路径优化

韩 印，师 攀 （上海理工大学，上海200093）

HAN Yin, SHI Pan (University of Shanghai for Science and Technology, Shanghai 200093, China)

0 引 言

我国每年果品腐蚀损坏近1 200 万吨，蔬菜1.3 亿吨，经济损失超过上千亿元。易腐食品特别是初级农产品的大量损耗，尤其在运输过程中损耗最高，使整个物流费用占到易腐食品成本的70%。因此，迫切需要降低物流成本。

优化配送路径是降低物流成本的重要途径。早在1959 年，Dantzig 和Ramser 在进行一个配送汽油至加油站的问题时就提出了车辆路径问题[1]。Clarke 和Wright 在此基础上提出了一种改进的并且较为有效的启发式算法，Clarke-Wright 节约算法[2]。1987年，Solomon 和Desrosiers 等人将时间窗约束引入到一般的车辆路径问题中，最早对时间窗的车辆路径问题进行了研究[3]。但是，对冷链物流配送路径优化的研究还相对较少，Tarantilies 和Kiranoudis 等认为时间的有效性是易腐食品配送的关键，提出通过交换路径中的节点或路径来进行改进算法优越性的后启发式算法，但是没有考虑冷藏[4]。Miroslav Verbic 用线性规划的方法，从经济价值角度给出衡量冷链中易腐食品质量的主要因素[5]。李宏以传统时间窗限制下车辆路径问题为基础，考虑了生鲜产品腐坏造成的货损成本以及违反客户需求时间窗引起的惩罚成本、配送时冷冻设备消耗的成本等，建立了冷链物流配送路径的基本模型，最后进行了算例分析和主要参数的敏感度分析[6]。上述文献都没有考虑路况条件，本文在冷链物流配送模型的基础上，考虑路况对配送路径的影响，构造了一种综合节约算法，并对10 个客户进行算例分析，用该算法分别对考虑路况条件的配送模型与没考虑路况条件的配送模型求解，由结果可知两个模型得出的最优路径不同，因此得出结论，研究考虑路况条件的冷链物流配送更具有实际意义。

1 冷链物流配送模型

1.1 问题描述

冷链物流配送路径优化问题可描述为：一个配送中心拥有多辆汽车，每辆汽车从配送中心出发，为多个客户送货，配送结束后配送车辆返回配送中心。

1.2 模型前提假设

（1） 配送中心拥有一定数量的配送车辆，且每辆车载重量一定。

（2） 配送中心不存在缺货，且客户的需求量、地理位置、时间窗约束已知。

（3） 配送车辆从配送中心出发，完成配送任务后必须返回配送中心。

（4） 车辆一旦离开前一个客户点，下一个客户点便已确定，无中途指派。

（5） 在配送过程中能保持固定温度，产品损耗只与配送时间有关。

（6） 每条路线上的需求量都小于车辆的装载量，且每个客户所需货物只能由一辆汽车配送。

（7） 每条配送路径上的运输长度不能大于配送车辆一次配送最大距离。

（8） 每个客户对早到或晚到的不满意程度都符合相同的线性函数关系。

（9） 每条道路等级已知。

1.3 冷链物流配送模型建立

模型以综合成本最低作为目标函数。综合成本包括：配送车辆的运输成本、货损成本、能耗成本以及违反时间窗的惩罚成本。

（1） 配送车辆运输成本

车辆的运输成本可表示为：

其中：c为单位里程运输成本，dij为客户i到客户j之间的距离，xijk为0，1 变量，当第k辆车经过（pi,pj）路段时，则xijk为1，否则为0。

（2） 配送过程中的货损成本

货损成本包含运输过程中的货损成本和服务客户时车门开启造成的货损成本。货损成本可表示为：

其中：p为生鲜产品的单位成本，xjk为0，1 变量，当第K辆车为j客户服务时，xjk=1，否则为0。dij为从客户i到客户j的距离。zij为路况条件转换系数，θ1为运输过程中的货损系数，θ2为服务客户时的货损系数，qj为到达客户j时车上所剩的货物量。

（3） 配送车辆制冷的能耗成本

制冷剂消耗量计算简化公式为：

其中：H为制冷剂消耗量，β 为常数，R为车厢的热传系数（W/（m2·K），Sb为车体表面积（m）2，ΔT为车厢内外温度差（℃）。设ph为制冷剂价格，则车辆行驶过程中消耗制冷剂成本为：

打开车门时消耗的制冷成本为：

其中：fj为车辆在客户j的服务时间，S为车门面积。

（4） 违反客户时间窗的惩罚成本

假设客户j要求的时间窗为[ej,lj]，可接受的时间窗为[Ej,Lj]，tj为配送车辆到达客户点j的时间。如果送达时间在[Ej,lj]，惩罚成本为0；如果送达时间超过[Ej,Lj]，则惩罚成本为+∞；若在Ej之前则需要等待至Ej，期间货损系数为θ1；如在[lj,Lj]之间送达，惩罚系数为μ。因此，惩罚成本可表示为：

1.4 冷链物流车辆配送路径优化模型

上述式中式（1） 为目标函数；式（2） 约束配送路径数不能超过配送车辆总数；式（3） 约束配送车辆的出发点和返回点都为配送中心；式（4）、（5） 约束每个客户只被一辆车服务一次；式（6） 约束每条路径上客户需求总量不得超过配送车辆的载重量；式（7） 要求车辆到达时间必须在客户要求的时间范围内；式（8）、（9） 保证时间表的灵活性。

2 基于路况条件下的综合节约算法

综合节约算法与原有节约里程法的不同之处是不单纯的以距离作为节约的判断依据，而是综合考虑了道路状况，将距离节约转化为综合节约。

综合节约的基本思想是综合考虑配送道路通行状况，并通过当地交管部门获取道路状况系数zij，通过道路平均运行速度进行换算，然后对运输成本、货损成本、制冷成本分别节约，最后对其进行综合，如表1。其方法如下：

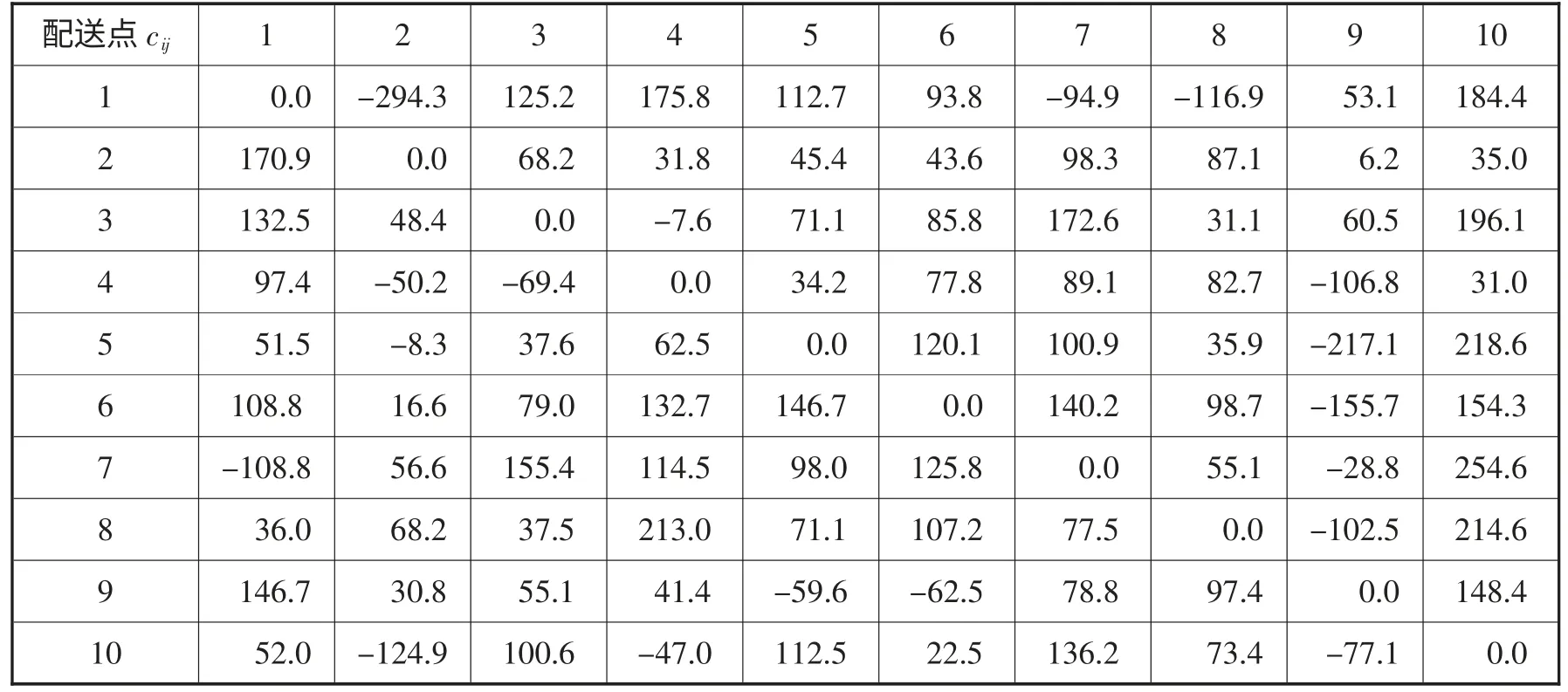
表1 综合节约成本

（1） 每一个节点pi与配送中心p0连接，产生n条仅含一个点的路径p0-p1-p0，根据节约算法，连接任意两点i、j后算出节约运输成本Δc1=c0i+c0j-cij。然后依次算出节约货损成本节约制冷成本

（2） 将三个节约成本进行综合得到总节约成本Δc=Δc1+Δc2+Δc3。

（3） 以时间窗为标准，将所有客户依次排序。

（4） 以配送中心为起点，将时间窗最靠前的客户作为第一条路线上的第一个客户，并在Δc表格中找出总节约成本最大的客户。依此类推，直到达到时间窗或者车容量限制，这作为第一条路线。

（5） 删掉第一条线路上的客户，重复步骤4，直到所有客户都在线路上。

3 算例分析

本文给出10 个客户数算例验证上述算法，具体描述如下：某配送中心向10 个客户配送某种蔬菜，客户i的需求量为Qi，配送中心到各配送点的需求量和配送距离由表2 给出，在i的服务时间为fi以及客户要求到达的时间范围[ej,lj]由表3 给出，采用小型货车的载重量为4t，且配送过程中平均行使速度为30km/h，最后返回配送中心。

单位运输成本c=2 元/km，蔬菜单价为4 000 元/t，运输过程中的货损系数θ1为3%，装卸过程中的货损系数θ2为0.2%，车内温度为-20℃，车外温度为30℃，车辆使用液态氮为制冷剂，每千克制冷剂价格为4.5 元，β=0.19,ph=4.5，R=0.4,sb=16, Δt=50。

结果分析：

根据产品配送的具体要求，运用改进后的节约算法对问题进行求解，得到的优化结果为：

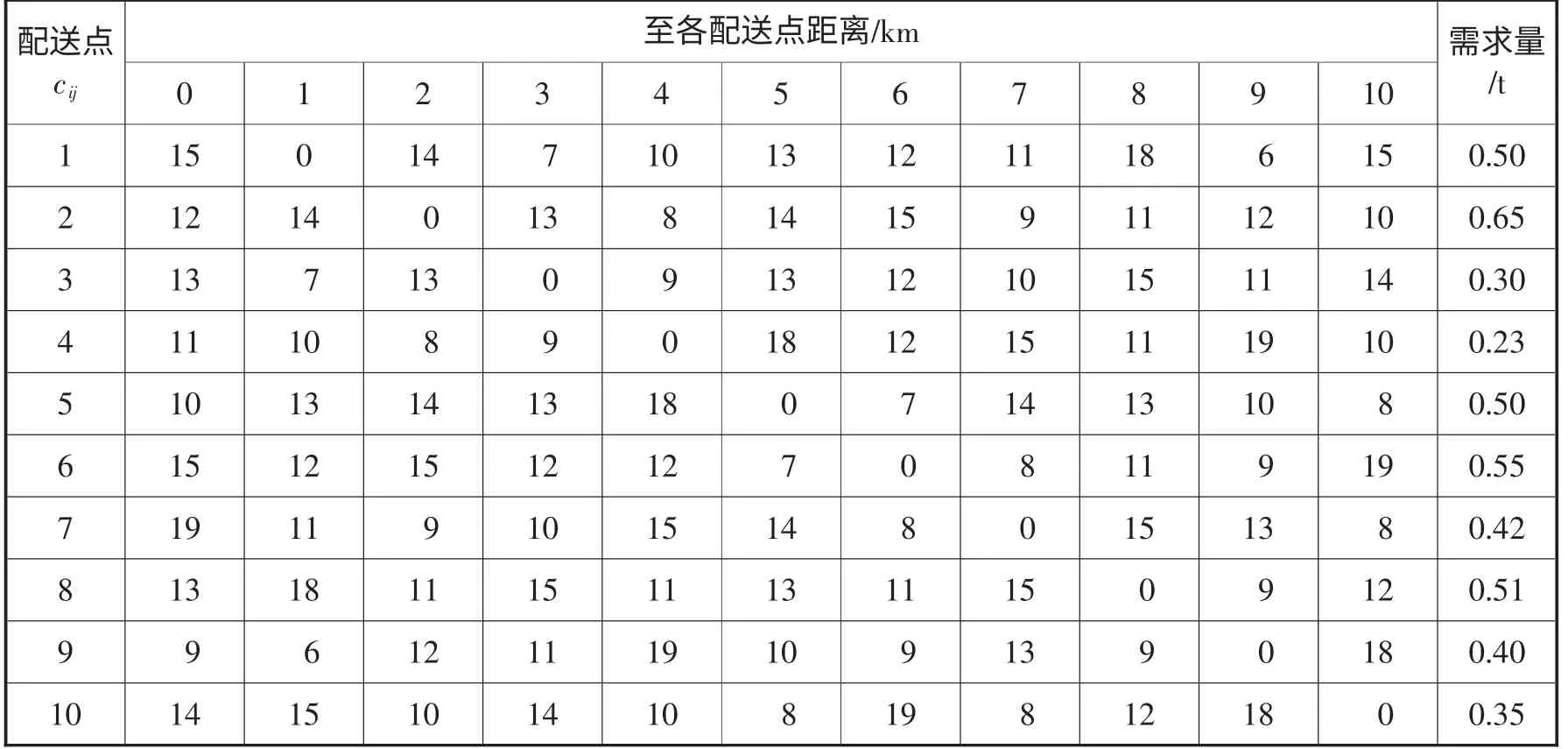
表2 配送距离及各配送点的需求量

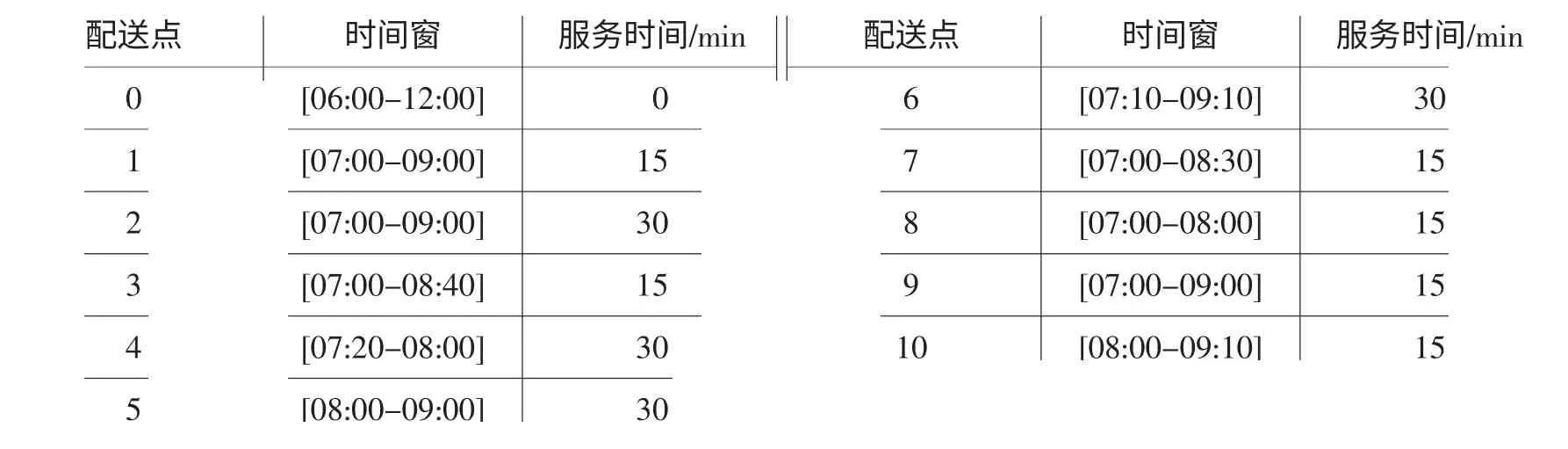
表3 各配送点的时间窗及服务时间

下面根据没有考虑路况条件的车辆配送模型，利用上述算法求出最优路径，并把所得路径给出以供比较。

比较上述路径可知：两个模型所得路径完全不同，考虑道路状况的模型将实际配送的道路状况考虑在内，更加具有实际意义。

4 结 论

本文在一般冷藏配送模型的基础上，充分考虑了实际道路状况，通过将道路状况进行简单的转化，构建了考虑道路状况的冷藏物流配送路径优化模型。模型以包括制冷成本、运输成本、货损成本、违反时间窗的惩罚成本在内的总成本最小为目标函数，以车载重量、时间窗为约束。在算法上，构建了基于道路状况的综合节约算法，并用该算法找出一个10 个客户算例最优路径。最后通过比较一般冷藏物流配送模型跟考虑实际道路状况的路径优化模型所得到的最优路径进行比较，可知两个模型求出的最优路径是不相同的，从而得出建立考虑道路状况的冷藏物流配送模型更加具有实际意义。

[1] Dant Zig G, Ramser J. Theruek dispatehing problem[J]. Management Seienee, 1959(6):80-91.

[2] Clark G, Wright J. Seheduling of vehieles from aeentral depotto anumber of delivery Points[J]. OPens, Researeh, 1964(4):15-18.

[3] Solomon, M. M.. Algorithm for the Vehiele Routing and Seheduling Problems with Time—Windows Constraints[J]. OPerationsreseareh, 1987(2):254-265.

[4] Tarantilis C D, Kirannoudis C T. Ameta-heuristic algorithm for the efficient distribution of perishable foods[J]. Joumal of Food Engingeering, 2001,50:1-9.

[5] Miroslav Verbic. Discussing the parameter of preservation of perishable goods in a cold logistic chain model[J]. Applied Economics, 2006,38:137-147.

[6] 李宏. 城市冷链物流配送车辆问题的研究[D]. 长沙：长沙理工大学（硕士学位论文），2006.