基于改进节约算法的集送货车辆路径优化

闵嘉宁，金 成 （无锡太湖学院，江苏 无锡214064）

MIN Jia-ning, JIN Cheng (Taihu University of Wuxi, Wuxi 214064, China)

1 概 述

带集送货的物流可以减少单集货和单送货情况下车辆“空跑”所带来的消耗，减少运输成本，降低流通成本，增加企业效益，近年来广泛应用于电子商务中，成为物流行业发展的新潮流。

物流配送车辆优化问题（Vehicle Routing Problem, VRP） 是由Dantzig 和Ramser 于1959 年提出的，早年此类问题只是单纯的集货或者送货，并没有将二者结合起来[1]。为了更好地解决实际应用中的问题，将VRP 问题扩展为带回程取货的车辆路径问题（Vehicle Routing Problem with Backhauls，VRPB）[1-2]，并对其进行了分类，其中集送货同时进行的VRP 问题（Vehicle Routing Problem with Simultaneous Delivery and Pickup，VRPSDP）[2]是指对一系列集送货点，组织适当的行车路线，使车辆有序地通过它们，并最终返回配送中心；在满足一定的约束条件下，使得费用最少，也称为带集送货的路径优化问题。

VRP 属于NP-hard 问题，实际应用中多采用启发式算法和元启发式算法，其中由Clarke 和Wright 于1964 年提出的C-W节约启发式算法由于概念清晰、容易实现、很受企业欢迎。但是，在实际应用中，往往存在多个约束条件、多个优化目标，尤其是带集送货和时间窗的引入要求对C-W 节约算法进行改进以适应新的需求。目前国内对于带集货送货车辆路径规划的研究主要有：郭耀煌、李军[3]采用网络启发式算法进行了研究，并提出了考虑到每项任务，由其集货点至送货点为重车行驶，故将一项任务由两个点看成是一个点，称为重载点，从而简化了模型的规模。霍佳震，张磊[4]把上述问题分解为两个阶段进行求解：第一阶段对每一项任务内部的集货点与送货点进行内部安排行车路线；第二阶段再对各项任务之间进行外部安排行车路线，以此简化问题。钟石泉，贺国光[5]提出一种改进的禁忌算法来解决这类问题。李华[6]建立多目标优化模型，提出了先对各个目标进行无量纲处理，之后通过加权的方式将多个目标转化为单个目标作为适应度函数，用混合遗传算法进行仿真求解。陈鑫，王明阳，张丽华[7]采用遗传算法，在初始种群形成之前，将各个任务的送货点按时间窗进行排序的办法，求解了多配送中心带软时间窗的路径优化问题。冯芳媛[2]采用节约算法和禁忌搜索算法来解决多配送中心带逆向物流的多车型装卸混合路径优化问题。

研究了近年来国内学者解决VRPSDP 的方法，较少使用节约算法单独求解。本文根据课题需要，探索节约算法在解决这类问题中的可行性和实用性。设定送货与集货均无优先权，实现边配送边集收的运输模式，对有时间窗带集送货的VRP 进行建模；汲取已有的研究成果的精华，对节约算法进行改进，使得在满足时间窗的条件下，里程数最少并尽可能最大程度地利用车辆的载重能力、使用车辆数最少；通过实例验证，说明算法的合理性和有效性。

2 问题描述以及数学建模

VRPSDP 问题描述为：配送中心以及n个客户以点i（i=0,1,…,n）表示，其中配送中心编号为0；各点位置或各点之间距离已知，dij表示客户i到客户j的之间的距离；配送中心拥有足够的运载能力且车型一样，各货车的载重量为Q，客户i的送货量wi＜Q、集货量pi＜Q；tij表示车辆从客户i行驶到客户j的时间，sj表示运货车辆到达客户j的时间（也即客户j卸/装货任务的开始时间），Tj为完成装/卸货任务所需的时间；车辆从配送中心出发，完成配送和集货任务后装载收集的货物返回配送中心。要求在满足载重约束和时间约束的前提下货运的最短行车路线。载重约束为：一条线路上客户的总货运量（集/送货量） 不大于货车的载重量Q；时间约束为：运货车辆到达客户j的时间sj需要在一定的时间范围[ETj,LTj]内，其中ETj为到达的最早时间，LTj为允许到达的最迟开始的时间；如果提前或者迟后到达，则进行惩罚。

考虑到实际应用中的复杂情况，做如下假设：（1） 集货没有专门设定时间要求，在送货的同时完成，即，边送货、边集货；送货可以根据实际情况，设定时间约束或不设时间约束。（2） 在满足车辆装载量（或容积量） 的前提条件下尽可能多的满足客户的集送货量。（3） 在满足最短行车路径的情况下，车辆行驶里程最少、费用最省；车辆的使用数量最少、用车启动费用最少。（4） 当运输车辆为多种载重量时，选择载重量较大的作为首先调度的重量约束，以保证用车数量最少。（5） 在以配送货物为主、集收货物为辅的调度目标中，只有当车辆的装载量空余时才能集货，如果集货不能完全装载，则需要考虑集货积压惩罚（惩罚系数*积压货物重量/体积）；如果配送和收集货物作为共同的约束条件，则不再存在积压的问题。

目标函数：

其中：式（1） 为目标函数，使车辆在完成全部配送任务时所需要的最短运行距离。式（2） 为点j的客户由车辆k完成的唯一性约束。式（3） 为到达某个客户的车辆唯一性约束。式（4） 为客户对配送车辆的时间窗约束。式（5） 为车辆的载重约束，即某辆车所访问的全部客户的总送货量和总集货量都不能超过车辆本身的载重量，出发时车辆上都是需要配送的货物，而返回配送中心时车辆上都是收集的货物。式（6） 为路径中各点客户的装载量（送集货量之和） 不能超过车辆本身的载重量：假设，第k辆车、路径为（0,1,…,α-1,α,…,β,0），车辆到达当前点ijk=α，那么，α 点前（1,…,α-1）个客户的总集货量与第（α… β）个客户的总送货量之和不大于车辆的装载量；配送和收集的货物可以混装。

3 C-W 算法的改进

C-W 算法的基本思想是：首先构建一个从配送中心到各客户点的单点的回路集，然后从一个回路开始，每次根据某个判别函数来确定将一个不在回路上的点增加进回路，以满足约束的要求，得到一个较满意的配送回路，直到所有的点都被安排进回路为止[8]。根据VRPSDP 的要求，对基本的C-W 算法进行了改进。

首先，改进算法增加了数据预处理。考虑到集送货的要求，在开始进行计算之前，首先判断各点需求量wi和集货量pi是否超出车辆的最大装载容量Q，如果超出，需要在Q的范围之内对该点单独送集货，而剩余部分再参加运算。

其次，下列步骤中，步骤4（点归并）、步骤5（载货量判断） 和步骤6（时间窗约束时点插入规则） 针对传统的节约算法进行了改进。具体如下：

步骤1 形成一个初始解。采取单点配送构成各车辆配送点集L1,L2,…,Ln，令Li=｛i｝，i=（1,2,…,n）。

步骤2 进行节约度的计算。计算所有点对（i,j）的节约度然后对计算结果进行降序排列。

步骤3 构建新的初始回路集L'0=Ø 和重量集R'0=0。

步骤4 按照节约里程△dij队列从大到小的顺序，直至队列为Ø，分析点对（i,j）合并进入路径的可能性：如果队列不为Ø，而（i,j）合并的可能性不存在，则转步骤3，开始构建一个新的路径。点对（i,j）合并进入路径的判断条件如下：

（2） 若（i,j）中有一个点是回路中的首或尾而另一个点不在回路中则考虑合并计算回路的里程数，然后转去步骤5：

①若i是回路末端，则j合并在i点之后；

②若i是回路首端，则j合并在i点之前；

③若j是回路首端，则i合并在j点之前；

④若j是回路末端，则i合并在j点之后。

（3） 在有时间窗约束的情况下，若（i,j）中有一个点是回路中的点而另一个点不在回路中则考虑合并转去步骤5。

步骤5 考虑配送货和集收货共同作为载重约束，如果满足下列条件则转步骤6，否则返回步骤4，取下一个点对；

（3） 当前ijk点载重量（4） 考虑到节约算法的求解过程中重量是按照归并点逐点累加的，因此，在程序实现时，进行了假设，假设初始（满载了所有的配送货物），于是条件③归纳为：

当ijk=1：

因此，w1≥p1

当ijk=2：

因此，w1+w2≥p1+p2

如果以配送货物量为主约束条件、集收货量仅仅是采用“量力而为”的策略，则采用两阶段算法：第一阶段，只需考虑条件（1），运用节约算法，计算出配送路线；第二阶段，对第一阶段进行分析，找出可以顺路“捎带”集收货物的数量，然后对不能“捎带”的集收货物进行积压惩罚。

步骤6 转换时间约束为里程约束，里程约束为：

其中，ζ 为行驶速度；ζ*si为从源点到i点行驶的路程；ζ*tij=dij；ζ*Ti为i点的卸货时间对应的里程；ζ*ETj为提前到达的里程约束；ζ*LTj为迟后到达的里程约束。

里程约束的判断条件如下：

（3） 如果ζ*ETj＞ζ*sj＞ζ*LTj，或者ζ*ETi＞ζ*si＞ζ*LTi，则返回步骤4，取下一个点对。

4 实例验证

案例1：

假设某企业在某一区域内建有1 个配送站点，每辆车的车型都为650，某一时间段有16 个需要服务的顾客，客户的配送量和集货量以及点对之间的距离见表1、2，要求在配送站点中合理选择车辆并安排行驶路线使总费用最小。

表1 案例1 客户集送量

表2 案例1 客户点对间距离

采用上述改进的节约算法，以配送和集收货物量共同作为载重的约束条件，得到的结果如图1 和表3 所示。

表3

以配送货物量作为载重量的约束条件，先求得配送路径，然后，再分析集收货物量的可能性、进行惩罚处理。第一阶段得到的路径结果仍然如图1 所示。分析集收货物的可能性：3、7、12、14 点分别在各路径的接近末端，此时配送货物已经基本卸载，所以装载不超重的集收货物是可能的。该案例的集收货物点少，采用两阶段算法是可行的，但是，当集收货物点遍布在各客户点时，两阶段算法几乎是不可能的。案例2 可以说明这一点。

案例2：

假设某企业在某一区域内建有1 个配送站点，每辆车的车型都为10 吨，某一时间段有17 个需要服务的顾客，客户的需求量或退货量以及点对之间的距离见表4 和表5，要求在配送站点中合理选择车辆并安排行驶路线使总费用最小。

表4 案例2 中各客户的集送量

采用本文改进的节约算法、配送和集收货物量共同作为载重量约束，无时间约束的运行结果如表6 所示。结果表明改进算法的运行里程和用车数量比常规的节约算法都得到了减少：里程数减少了138，约10.7%；用车数已经达到了最少，每条路径都是满载送货，减少了用车费用和人力成本。然而，如果仅以配送量作为载重量的约束，运行结果的路径为：0-7-8-11-3-15-14-17-9-0，0-5-16-4-0，0-7-10-0，0-12-13-0，0-2-0，0-6-0，不可能满足集收货物的要求。

有时间约束的运行结果如表7 所示。结果表明改进算法的运行里程和用车数量比常规的节约算法都得到了明显减少：里程数减少了106，约7.5%；用车数减少了一辆，减少了用车费用和人力成本。

上述案例表明，采用改进的节约算法可以实现VRPSDP 的要求：①按照需求的送货量和集货量同时进行配送和集货。②送集货在时间窗约束之内。③车辆行驶里程数尽量小（节约算法本身内在性保证了里程数尽量小）。④车辆数尽量少（文中载重量的约束内在性的保证了使用车辆尽可能少）。与文献[2]相比有较好的结果。但是有时间约束的优化还不很理想，点2 未能进入运算，这是下一步研究需要解决的问题之一。

表5 案例2 中各客户的距离

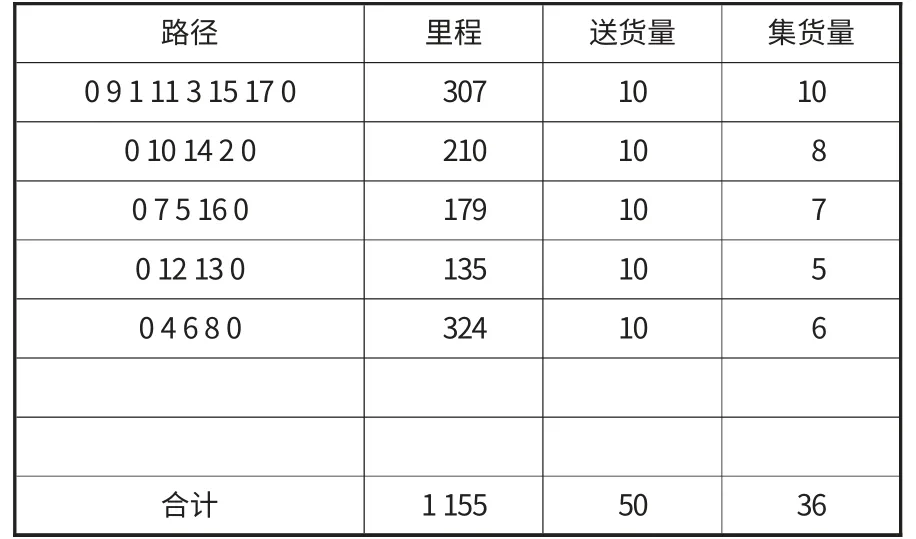
表6 无时间约束运行结果

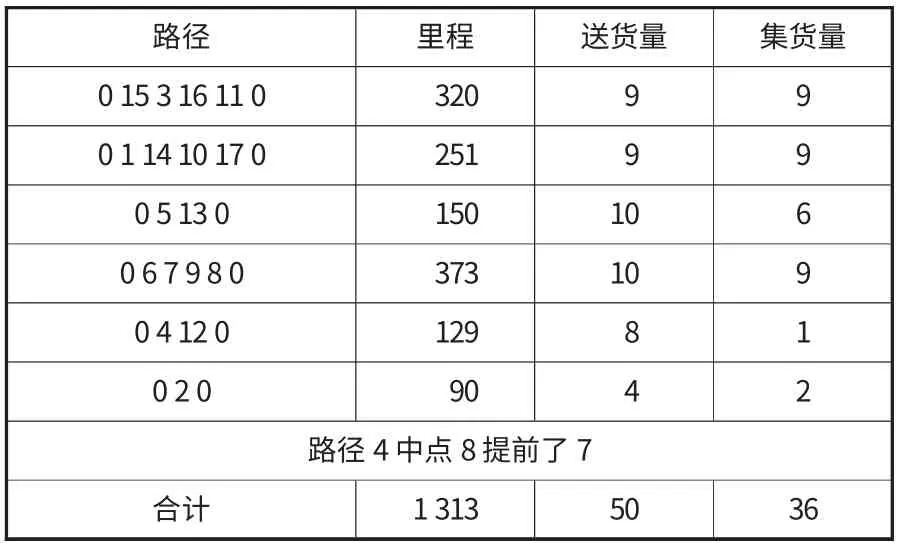
表7 有时间约束运行结果

5 结 论

本文从改进C-W 节约算法入手，对有时间窗约束的VRPSDP 模式进行了研究，提出了以集货量和送货量共同作为各客户点归并的判断条件，把时间窗约束转化为里程，针对有时间约束和无时间约束不同的条件提出了不同的归并规则，实验表明，文中所提出的算法实现了多个目标（里程、带集送货、载重、时间窗） 的路径优化，获得了较好的优化结果。

[1] 陈志忠，杨信丰，李引珍. 逆向物流综合回收问题的建模研究[J]. 兰州大学学报，2011,30(4):100-105.

[2] 冯芳媛. B2C 电子商务中带逆向物流的车辆路径优化问题研究[D]. 沈阳：沈阳师范大学（硕士学位论文），2011.

[3] 李军，郭耀煌. 物流配送车辆调度理论与方法[M]. 北京：中国物资出版社，2001.

[4] 霍佳震，张磊. 有时间窗的集货送货一体化车辆路径规划启发式算法研究[J]. 物流技术，2004(5):64-66.

[5] 钟石泉，贺国光. 有里程和时间窗约束的一体化车辆调度智能优化[J]. 系统工程与电子技术，2006,28(2):240-243.

[6] 李华. 具有同时配送和回收需求的车辆路径问题研究[D]. 成都：西南交通大学（硕士学位论文），2012.

[7] 陈鑫，王明阳，张丽华. 有里程和软时间窗约束的开放式多车场带集送货化车辆路径问题研究[J]. 物流科技，2012(12):28-31.

[8] 宋伟刚，张宏霞，佟玲. 有时间窗约束非满载车辆调度问题的节约算法[J]. 东北大学学报，2006,27(1):65-68.