基于客户满意度的多目标货物配装问题研究

文/李小玲 吴爱萍

基于客户满意度的多目标货物配装问题研究

文/李小玲 吴爱萍

本文在传统的货物配装模型的基础上引入客户满意度因素，从货物配装引起的货损率对客户满意度的影响角度建立以货损成本最小化以及车辆载重和容积利用率最大化为目标的多目标货物配装优化模型。

货损率；客户满意度；多目标；货物配装优化

引言

流通型配送中心主要是服务于商业企业的货物配送，这种货物配送往往属于一对多的配送形式，即由一个配送中心将货物配送个m个客户。而货物配装是配送的一个必经且重要的环节，学术上属于相当复杂约束条件的组合优化问题，属于NP～hard问题[1]。

在进行货物配装的过程中不可避免地会出现由于包装、装卸搬运以及货物放置位置不当造成实际的货物损坏，货物损坏的程度直接影响了客户对于物流企业的客户满意度。纵观国内外关于货物配装的模型，在货物配装的建模过程中，所考虑的约束条件比较少，大部分都只考虑货物的体积和重量约束[2～4]。此外，可以发现关于货物配装的建模，都是从企业、车的角度设立目标函数，没有从客户的角度如从客户满意度这个目标出发建立模型。

本文即从货物配装引起的货损率与客户满意度的背反效应这个角度，以最大化客户满意度的目标出发来研究多目标的、考虑客户满意度的多车多品种货物配装问题。

1.货损率与客户满意度关系

货物配装这一过程中，货物损坏主要是来自包括装卸搬运不当导致货物在装载工具内堆码方式不当造成货物挤压、刺穿、撞击、颠簸、倒塌或颠覆。

很明显，货损率与客户对物流企业的满意度呈负相关，货损率越高，客户满意度越低，货损率越低，相应地，客户满意度就越高[7]。因此，本文用货损率来衡量货物配装的客户满意度。客户对收到的货物完好程度在一个区间内是可以接受的，超过这个区间，客户对物流企业的满意度就会下降。将这个区间定义为货物配装货损率窗，如图1所示：Smax表示客户能够接受的最大货损率。货损率在在[0，Smax]这个区间内，则客户对物流企业完全满意，超出这个区间，客户满意度就为零[5]。

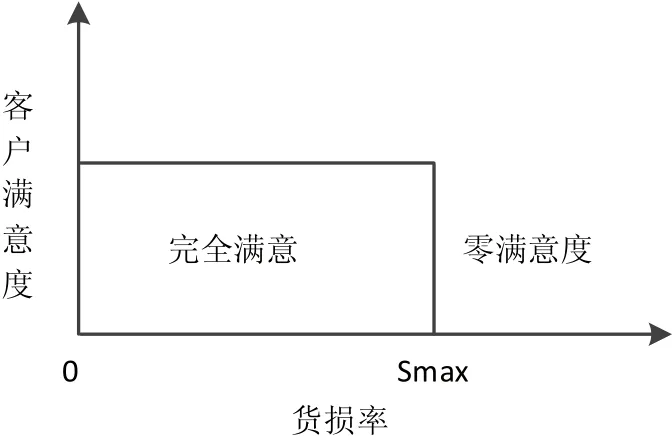
图1 货损率区间描述

2.模型构建

2.1 问题描述

基于客户满意度的多车多品种货物配装问题可以描述如下：有一物流配送中心，l为配送中心车辆的集合，k为车辆的编号，k=1，2，…，l；n为配送中心待装货物的数目，j为货物的编号，j=1，2，…，n；m为配送中心客户的集合，i为货物编号，i=1，2，…，m。配送中心在一定的货损成本条件下，满足客户需求以及配送中心车辆载重和体积利用率最高的货物配装方案。

2.2 目标设定

传统的货物配装问题多以车辆的载重和容积使用率最高为目标，本文结合顾客满意度与传统的目标，同时考虑到顾客满意度与货损率的关系，可将基于客户满意度的多车多品种货物配装问题的目标设定为如下3个：（1）货损成本最小化；（2）车辆载重利用率最大化；（3）车辆容积利用率最大化，其中以货损成本最小化为主要目标。

2.3 客户满意度表示

前面已经提到了在货物配装问题中客户满意度与货损率之间的关系，因此客户满意度的最大化可用货损成本最小化来来进行定量表示。

当客户的货物受到损坏，但实际货损率小于客户能够容忍的最大货损率Smax时，企业根据单位赔偿价格和货物损失总量赔偿客户的相应损失，这是由于货物配装不当而支出的成本，本文称之为货损成本。而货损总量取决于货物总量和总的货损率[6]。以ai表示客户收到的货物的货损率，ps为每单位货物的赔偿价格；di为客户i的需求量，那么客户i由于货物配装造成的货损成本为psdiaixijk，模型基本假设：

（1）客户收到的货物中损坏的部分是由于货物配装过程中装卸搬运不当、货物在车辆内部堆码方式不当导致在运输途中损坏；

（2）货物不经过中转，直接由配送中心送往最终客户；

（3）由于货物配装造成的货损率ai以及客户所能容忍的最大货损率Smax都是正态分布随机变量。之所以这样假设，是因为通过对以往客户对货损率要求和实际货损率情况进行统计分析，可以得到关于货损率的大量统计数据，再对这些数据进行合理地拟合，就得到了货损率的分布形式。由于正态分布的适用条件为：变量受多个微小的，独立的随机因素影响，而每个因素都不具有压倒一切的主导作用。货损率具有这一特点，因此这类变量服从正态分布的假设是成立的[6]；

（4）每个客户所需货物不能分割；

（5）只装载车辆有载重量和体积的上限，所配送的货物形状标准，排除由于农产品形状各异而可能形成的空隙；

（6）不考虑装入同一辆车车内的货物之间的相互影响，即产品之间都可以混装。

2.4 变量定义

gij：表示客户i的第j件货物的重量；

vij：表示客户i的第j件货物的体积；

xijk：为{0，1}变量，等于1则表示客户i的第j件货物由车辆k装载；否则；

yk：为{0，1}变量，等于1则表示车辆k被用来装载货物；否则；

Gk：为车辆k的载重量；

Vk：为车辆k的容积；

hi：为客户i给定的服务水平

2.5 模型建立

建立基于客户满意度的多车多品种货物的数学模型如下：

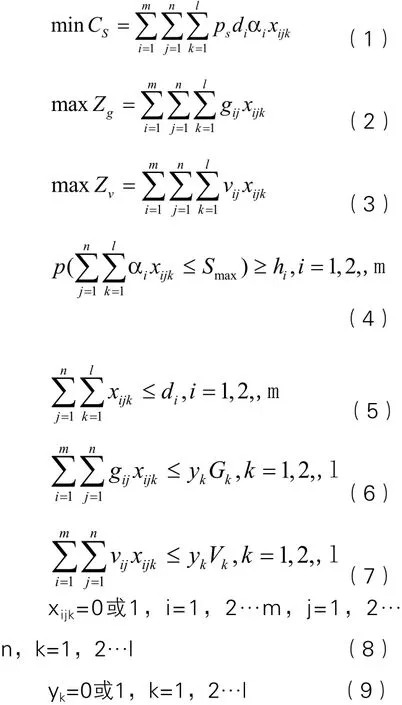
式中，式（1）～（3）中表示货物配装优化问题的目标；约束条件（4）表示客户对货损率限制的概率不小于给定的服务水平；约束条件（5）表示配送中心的货物配送量不超过客户的需求量；约束条件（6）表示每辆车装载的货物不超过车辆的载重量约束；式（7）表示每辆车装载的货物不超过车辆的容积约束；约束条件（8）表示每个客户的货物只装一辆车的约束；约束条件（9）表示车辆被选中的约束。

2.6 算法实现

对于上述多目标货物配装问题的求解，可以参考R.Cheng和M.Gen在解决模糊VRP问题的混合遗传算法来实现。这个方法使用push～bump～throw过程来处理问题模糊特征的插入启发式操作可以有效地求解与之类似的问题[7]。

3.结束语

本文从货损率与客户满意度背反这一点出发，以货损成本最小来代替客户满意度最大化目标，在此基础上建立基于客户满意度的货物配装优化模型，希望对货物配装问题的研究能够起到一定的推动作用。但本文还存在一些不足之处，由于个人能力的有限，还没找到一个很好的算法来实现这个模型的求解，是文章下一步需要仔细探讨的方向。

[1]曹明兰．配送中心货物优化配装问题的模型与算法研究[D]．武汉理工大学，2009：6～8．

[2]胡贵彦等．货物配载方法最优化研究[J]．物流技术，2009，28（8）：86～89．

[3]谢天保．物流配送中心配载车辆调度问题研究[J]．计算机工程与应用，2010，46（36）：237～240．

[4]李江萍，但斌，陈军．基于货损约束的配送系统优化模型[J]．工业工程，2006，9（6）：66～69．

[5]张建勇，郭耀煌，李军．基于顾客满意度的多目标模糊车辆优化调度问题研究[J]．铁道学报，2003，25（2）．

[6]李江萍．基于货损和时间约束的流通型配送中心配送作业管理研究[D]．重庆大学：23～25．

[7]Herrera F，Verdegay J． Genetic algorithms and soft computing[M]．Heidelberg：Physica～Verlag，1996．683～709．

广东理工学院质量工程项目，物流管理专业人才培养模式创新实验区，项目编号CXSY2016004

（

广东理工学院经济管理学院）