音圈电机超调控制研究

钱俊兵，杜礼霞，何祖顺

(昆明理工大学机电工程学院，云南 昆明 650500)

Research on Overshoot Control of Voice Coil Motors

QIAN Junbing，DU Lixia，HE Zushun

(Faculty of Mechanical and Electrical Engineering，Kunming University of Science and Technology，Kunming 650500，China)



音圈电机超调控制研究

钱俊兵，杜礼霞，何祖顺

(昆明理工大学机电工程学院，云南 昆明 650500)

ResearchonOvershootControlofVoiceCoilMotors

QIANJunbing，DULixia，HEZushun

(FacultyofMechanicalandElectricalEngineering，KunmingUniversityofScienceandTechnology，Kunming650500，China)

摘要：针对音圈电机作动器阶跃响应超调的问题，提出了一种简单有效的抑制控制技术。通过两次阶跃输入相互抑制规划，有效地抑制了作动器的超调问题，并分析了响应误差和两次阶跃输入信号间的关系。通过仿真和实验验证了驱动控制的有效性。

关键词：音圈电机；作动器；阶跃输入；超调；抑制

0　引言

作为直线电机中的音圈电机是一种将电能直接转换成直线运动机械能，而无需任何中间转换机构的传动装置。可以认为是旋转电机在结构方面的一种演变，它看作是将1台旋转电机沿径向剖开，然后将电机的圆周展开成直线。音圈电机采用“零传动”的直接驱动方式，改变了“旋转电机”加链条、钢丝绳、丝杠和蜗轮蜗杆等 “传动机构”间接传统驱动方式，把负载与电机直接连接，实现了动力源与负载的刚性直接耦合[1-2]。由于采用直接驱动方式，音圈电机驱动克服了传统旋转电机驱动带来的间隙、摩擦和碰撞等一系列的问题。因此，音圈电机具有结构简单紧凑、快速响应、良好的电流-推力性能、控制简单和无限的分辨率等优良特性，使音圈电机常作为精密电磁作动器应用于精密设备中，已成为精密驱动和传动领域的研究热点和焦点[3-5]。但是，由于直线驱动的结构方式也带来了新的问题，各种扰动不经过中间环节的机械衰减和缓冲直接加载到了音圈电机上，降低了音圈电机的伺服性能，因此，必须针对音圈电机的驱动系统进行研究[6-7]。

1　音圈电机结构及辨识

1.1音圈电机结构

音圈电机的结构如图1所示，可分为动子和定子2部分。如图1所示，定子由外形相似的两单元间隔而成，每一单元由多块永磁体按极性交错排列于导磁材料的磁轭表面，构成了电机的气隙磁场；动子主要由线圈绕组构成。

在音圈电机动子结构中，为了把线圈产生的洛伦兹力向外传递，把线圈绕制于金属线芯上。通过支撑块的固定和支撑作用，不仅把线圈固定于框架内，而且可把线圈电磁力通过线芯支撑块传递到框架上，从而向外进行传递。在动子框架的两侧覆盖2块陶瓷的薄板，对热量进行隔绝。音圈电机工作原理为通电导线置于磁场中受到的洛伦兹力，如果改变音圈电机通电线圈中电流的大小和方向，就可改变音圈电机推力的大小和方向。

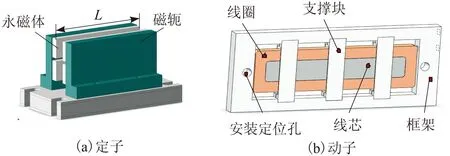
图1　定子和动子结构

1.2音圈电机系统辨识

音圈电机驱动控制结构如图2所示。在音圈电机驱动控制中，把驱动器和音圈电机作为一个整体，即作动器。作动器作为一个伺服单元响应来自控制系统的指令，对外界产生力或位移的输出。

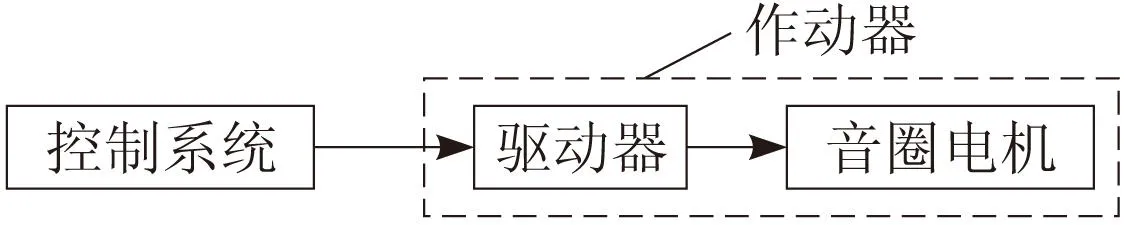
图2　音圈电机驱动控制系统结构

对作动器进行系统辨识，可获得作动器的传递函数表达式G(s)，即

(1)

ζ为阻尼比；ωn为无阻尼自然振荡频率；A为常数；s为拉式变换单位。

在音圈电机及其驱动器构成的作动器中，作动器对外界的出力是一个间断而短暂的过程，这时，控制系统对作动器输入的指令往往就是一阶跃信号及其集合，而所对应的响应便是作动器对阶跃电流信号的响应。如图3所示，在作动器中，没有使用控制策略时，作动器对阶跃输入电流的响应存在着明显的超调现象(输入阶跃幅值为2，输出响应为音圈电机线圈中流过的电流)。

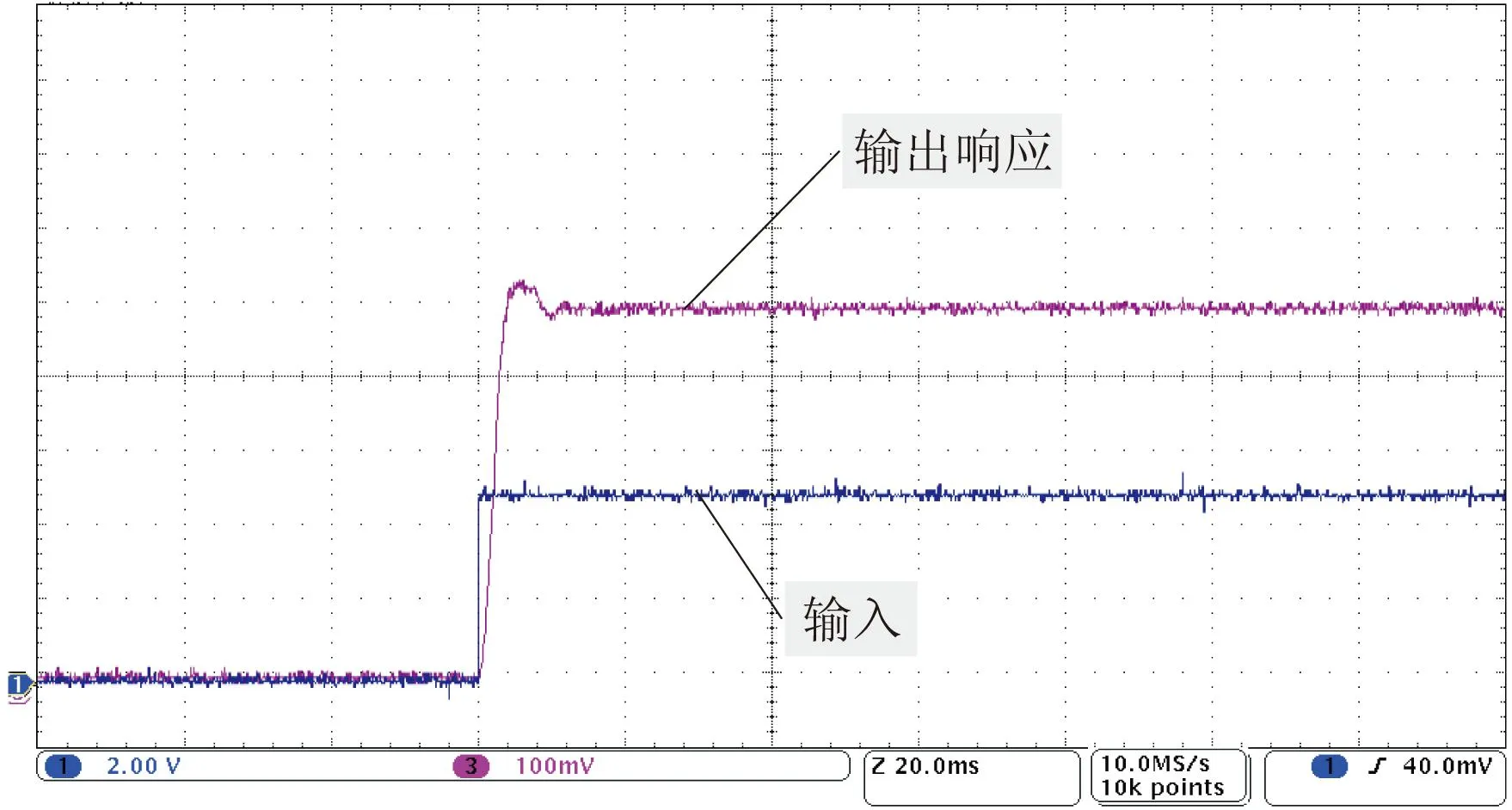
图3　实验结果

2　音圈电机阶跃控制

采用两次阶跃输入的相互抑制方式，其表达式为：

a1，a3为第1、2阶跃输入幅值；t为时间；β为初始相位；tw为延迟时间；c(t)为总输出；ca1(t)，ca3(t-tw)为阶跃输入响应；ωd=ωn(1-ζ2)1/2，为阻尼振荡频率；tp为第1个阶跃响应的峰值时间。

由上式可知，输出由2部分构成(分别位于2个中括号内)，即常数和正弦波动。而输出的超调正是由于正弦的第1(正超调)和第2个峰(负超调)引起，因此，控制输出的正弦波动就可很好地控制超调和波动。

根据实际工程中对输出稳定的误差E要求，假设系统允许存在的输出误差带大小为输入幅值的E%，即(a1+a2)E%。可得抑制第1个峰的约束式(2)及第2个峰的约束式(3)。

(2)

(3)

所以a1，a3的取值范围由式(2)和式(3)共同决定。

3　控制仿真与实验

为了对式(2)和式(3)进行验证，进行了Matlab/Simulink仿真及实验验证(取a=2A)。

3.1仿真分析

3.1.1 无控制策略

在无控制策略的情况下，作动器对阶跃输入的响应如图4所示。由图4可知，响应输出的超调约为输入的20%，而响应达到稳定的时间约为0.03 s(取E%=5%)。

图4　无控制策略的阶跃响应

3.1.2边界条件下的响应

把a=2A代入式(2)和式(3)，对超调的下边界条件下(a1=1.562 5A，a2=0.437 5A)的作动器响应进行仿真分析，结果如图5所示(取E%=5%)。

如图5所示，作动器输出响应稳定的时间为0.019 s，比无控制的响应先0.011 s达到稳定。同理，对超调的上边界条件下(a1=1.726 9A，a2=0.273 1A)的作动器响应进行仿真分析，结果如图6所示(取E%=5%)。作动器输出响应稳定的时间为0.015 s，比无控制响应先0.015 s达到稳定。由图5和图6可知，当输入阶跃信号时，采用了超调控制的作动器比没有采用超调控制的作动器更快进入稳定状态。

在2个阶跃输入的信号中，第1个阶跃输入信号的幅值较第2个阶跃输入信号的幅值大得多。由此，说明第1个阶跃输入信号是主要的输入信号，而第2个阶跃输入信号是对第1个输入的调整和修正。

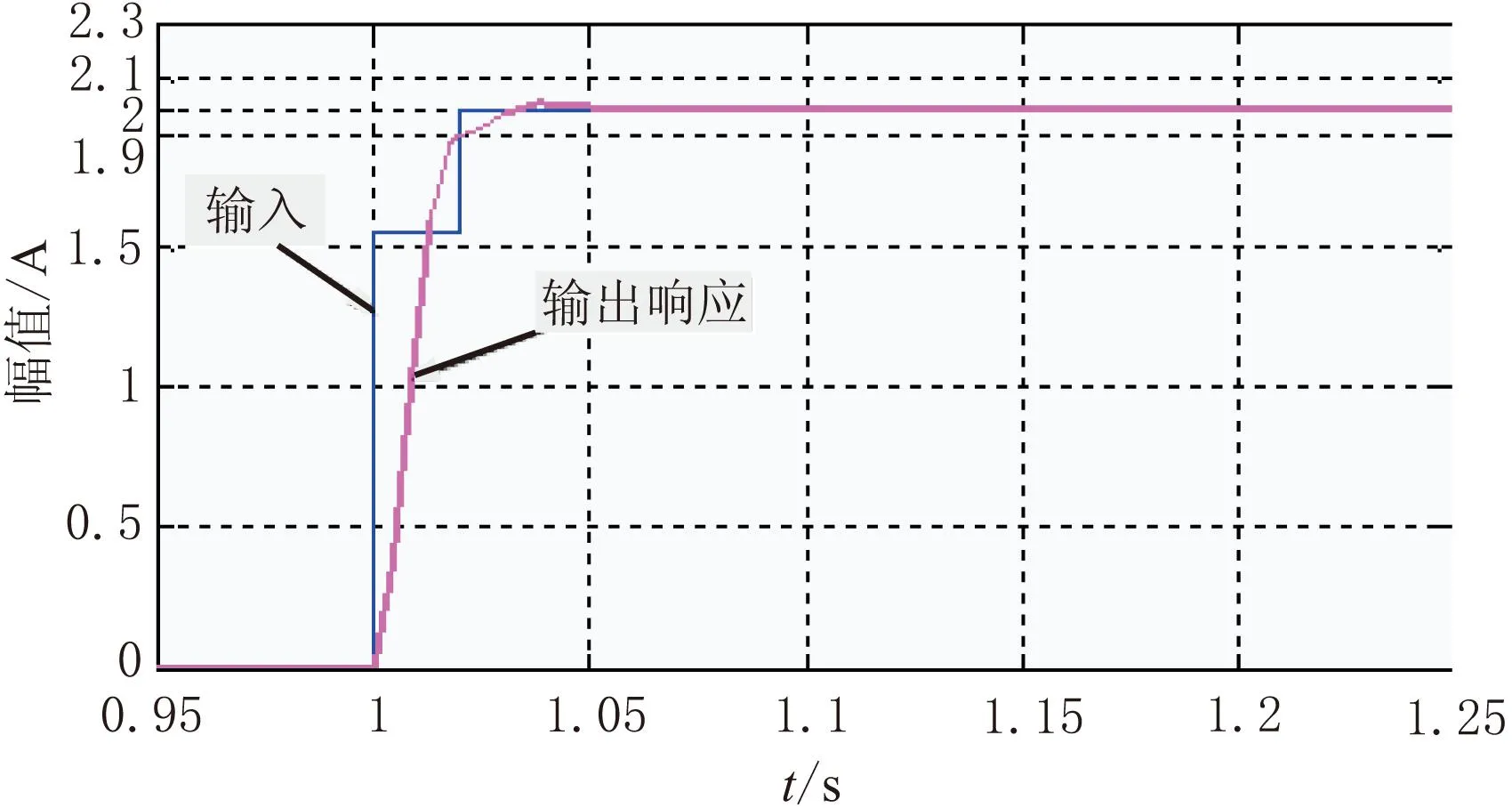
图5　 a1=1.562 5A，a2=0.437 5A时的阶跃响应

图6　a1=1.726 9A，a2=0.273 1A时的阶跃响应

3.1.3 误差为零时的响应

取E%=0时，输入阶跃幅值为2时，根据式(2)和式(3)可得相应的仿真结果分别如图7和图8所示。如图6所示，对于阶跃信号，作动器响应稳定的时间为0.016 5 s，比没有采用超调控制的作动器更快进入稳定。

图7　a1=1.644 7A，a2=0.355 3A时的阶跃响应

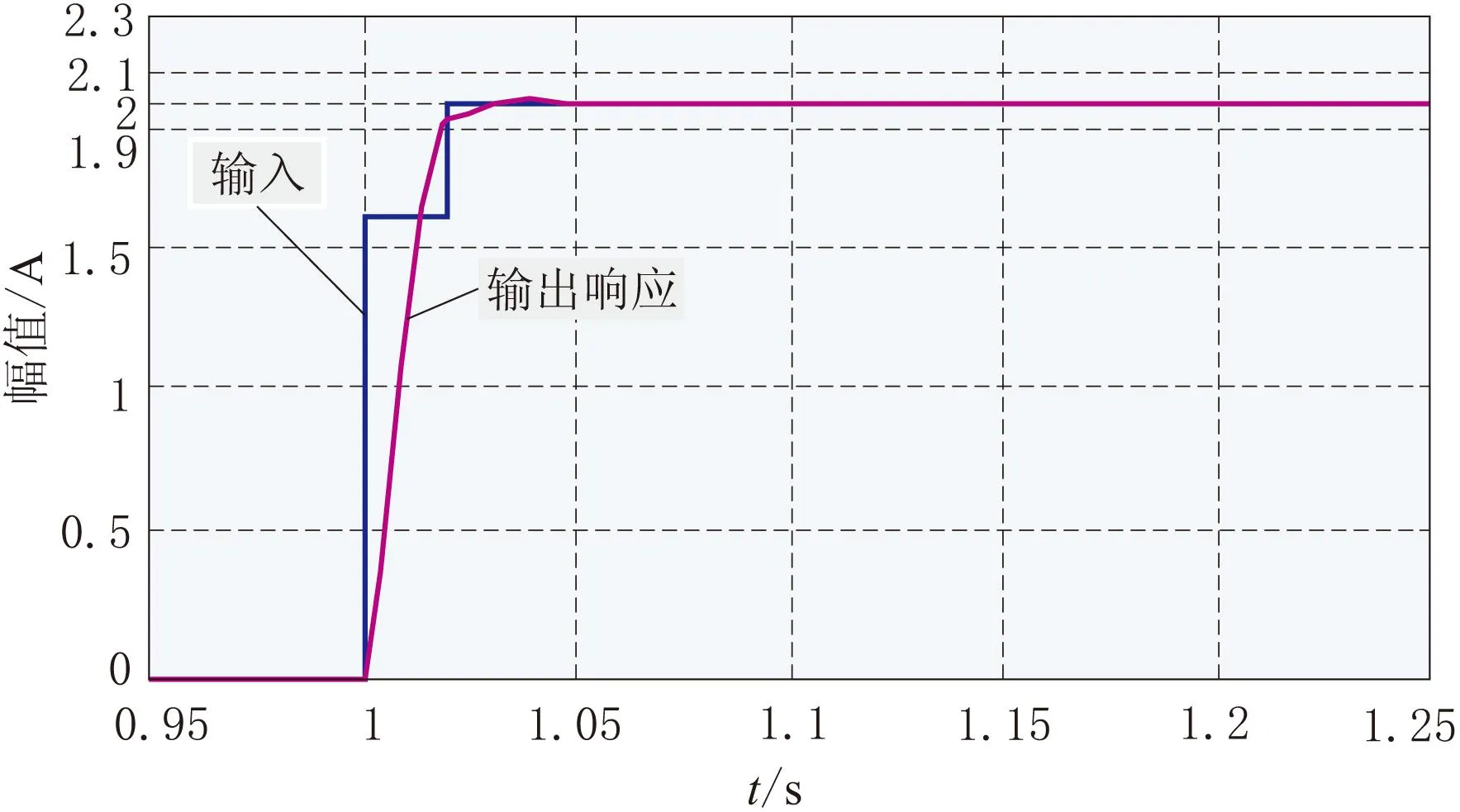
图8　a1=1.597 1A，a2=0.402 9A时的阶跃响应

以式(3)作为约束条件时，因为抑制的目标主要为第2个峰谷，输出响应在原第1峰附近出现了微小的波动，然后才进入稳定状态并维持稳定状态。

综合可知，在作动器对阶跃输入的响应中，如果以第1个波峰的超调为抑制目标，随后的输出就稳定了。如果以第1个波谷作为抑制目标，将不能完全消除第1个波峰超调的影响。

3.2驱动控制实验验证

为了对前面的分析进行进一步的实验验证，通过搭建的作动器实验平台(如图9所示)对作动器控制进行了实验验证。实验中取E%=0时，输入阶跃幅值为2。输出响应为音圈电机线圈中流过的电流。

对比图3和图10可知，对作动器进行抑制阶跃输入超调的控制，能有效地抑制响应的超调和波动，使作动器平稳地对输入进行响应。

图9　作动器实验装置

图10　采用控制策略的作动器响应

4　结束语

针对作动器阶跃输入响应的超调问题，从控制上进行了相应的分析，提出了带误差范围的2次规划输入方法。建立了推力响应超调、误差带和两次阶跃输入关系的数学关系表达式。为了验证作动器超调控制策略的有效性，利用Matlab/Simulink及作动器实验平台分别进行仿真和实验验证，结果证实了超调控制策略的正确性和有效性。

参考文献：

[1]Patterson D，Brice C W，Dougal R，et al.Design and simulation of a permanent-magnet electromagnetic aircraft launcher[J].IEEE Transactions on Industry Applications，2005，41(2):566-575.

[2]Chou P C，Lin Y C，Cheng S. Enhancement of optical adaptive sensing by using a dual-stage seesaw-swivel actuator with a tunable vibration absorber[J]. Sensors，2011，11(5): 4808-4829.

[3]Chen Y D，Fuh C C，Tung P C. Application of voice coil motors in active dynamic vibration absorbers[J]. IEEE Transactions on Magnetics，2005，41(3): 1149-1154.

[4]冯晓梅，张大卫，赵兴玉. 基于音圈电机的新型高速精密定位系统设计方法[J]. 中国机械工程，2005，16(16):1414-1419.

[5]范大鹏，范世，鲁亚飞，等. 数控机床高性能传动部件控制技术的研究进展[J]. 中国机械工程，2011，22(11):1378-1385.

[6]Alter D M，Tsao T C. Control of linear motors for machine tool feed drives: design and implementation of H∞ optimal feedback control[J].ASME Journal of Dynamic Systems，Measurement and Control，1996，118:649-656.

[7]Yao B，Xu L. Adaptive robust control of linear motors for precision manufacturing[J]. International Journal of Mechatronics，2002，12(4):595-616.

Abstract：For the thrust overshoot of voice coil motors that appears in response to step inputs, a simple and effective control strategy is investigated based on the method of restraining mutually by response. The thrust overshoot is solved effectively by the inputs, in which the original step input is divided into two step inputs with different amplitudes. An analytical formula is derived to express the relationship between the two step inputs and the output error. The effectiveness of the proposed method is verified by simulation and experimental results.

Key words：voice coil motors；actuator；step input；overshoot；restraint

作者简介：钱俊兵(1976-) ，男，云南文山人，讲师，研究方向为机电运动控制；杜礼霞(1977-)，女，云南文山人，讲师，研究方向为电气控制。

基金项目：云南省级项目(人才培养)(KKSY201401097)

收稿日期：2015-03-23

文章编号：1001-2257(2015)06-0026-04

文献标识码：A

中图分类号：TM359.4