基于内点法和拉格朗日乘子法的混合试验冗余作动器控制方法

王尚长， 杨 格， 吴 斌， 谭启阳， 杨少攀

(1. 武汉理工大学 土木工程与建筑学院，武汉 430070; 2. 哈尔滨工业大学 土木工程学院，哈尔滨 150090)

结构抗震试验是检验建筑结构抗震性能、探索抗震设计理论的重要工具[1]。随着我国建筑结构的不断发展，结构件尺寸不断增大，为了能更准确地模拟结构地震响应，试件的大型化、足尺化已成为必然趋势[2-3]。拟静力试验、地震模拟振动台试验[4-5]、拟动力试验[6]是目前最常用的三种结构抗震试验方法。其中，拟动力试验又称混合试验[7]，它可以经济有效地开展大型结构的抗震试验研究，因而受到了研究者的广泛关注。对于大型结构的足尺或者大比例尺拟动力试验，其试件刚度往往较大，为了满足出力要求，每个加载方向可能至少需要两台作动器。此时，作动器数量多于所要控制的试件自由度数量，即存在冗余作动器[8]。冗余作动器具有消除加载系统奇异、增加系统刚度和出力均匀等优点，通过采用冗余作动器，试验加载系统可以使用多个质量更轻、出力更小的作动器来实现加载。此外，在某台作动器失效的情况下，加载系统仍具有继续工作的能力，增加了试验的安全性。邱法维等[9]对单根柱进行了单向和双向的拟动力试验，试验表明水平双向地震作用对结构的危害更为严重，在双向试验中研究冗余作动器的加载控制具有重要的价值。

Meyer等[10]对机械手控制时采用最小能耗功率损失最小为目标函数，验证了此时设备承受很大内力。Molina等[11]为使各台作动器出力之和最小而提出一种约束方程，并且对作动器采用全位移控制策略完成了三层双向结构试验。Wu等[12]提出等效力控制方法，并利用力-位移转换系数将等效力转化为位移命令，对作动器仍采用传统位移控制方法完成了实时混合试验，Chen等[13]在此基础上对等效力控制方法进行了改进，并选取三层框架支撑的全尺度钢筋混凝土砌体剪力墙作为物理子结构进行了试验验证。武汉理工大学吴斌教授团队研发的一款混合试验软件HyTest[14-15]将加载控制方法整合到一起，并且完成了多种类型的混合试验[16]。在不存在冗余作动器的情况下，以上控制方法对单台作动器或试验采用了各种控制方法都获得良好精度，但是由于作动器与试件和反力墙的连接不可避免地存在滑移、变形等原因，在冗余作动器存在的试验仍然采用传统的控制手段将会对试验精度甚至试验安全产生很大影响。比如，柱子的单向试验，在柱顶一个方向上布置两台采用位移控制的作动器，由于滑移、变形等原因，位移命令使两台作动器互相掣肘，产生巨大内力甚至发生危险。

为了解决上述问题，王贞等[17]提出对冗余作动器采用力控制模式完成了单层单跨双向混合试验。本文在此基础上考虑作动器的出力范围，提出考虑作动器出力边界的冗余作动器控制方法，给出作动器系统能力可行域的求解方法；然后基于Simulink搭建了加载控制系统仿真平台，通过预先确定的运动轨迹模拟了冗余控制系统与非冗余控制系统工作状态，检验了冗余作动器的控制效果。最后对一个两层双向足尺结构开展了虚拟混合试验，验证了所提冗余控制方法的有效性，并给定了各台作动器最大出力参考值，可为相关人员在选择作动器吨位或型号时提供参考。

1 冗余作动器的控制

双向结构试验对象假定为单层单跨空间钢框架，楼板为正方形刚体，试件及作动器布置方案如图1所示。考虑楼板平面内的3个自由度，即两个平动位移和一个平面内的转角。采用4台作动器实现这3个自由度上的位移，本试验的作动器数量多于自由度数量，因此存在冗余作动器。将4号作动器定义为冗余作动器，采用力控制，其余3台作动器则为非冗余作动器，采用位移控制。本试验的加载控制点[18]为楼板的质心，通过建立楼板质心与非冗余作动器伸长量之间的关系，以及楼板质心恢复力与冗余作动器出力值之间的关系，实现双向试验。

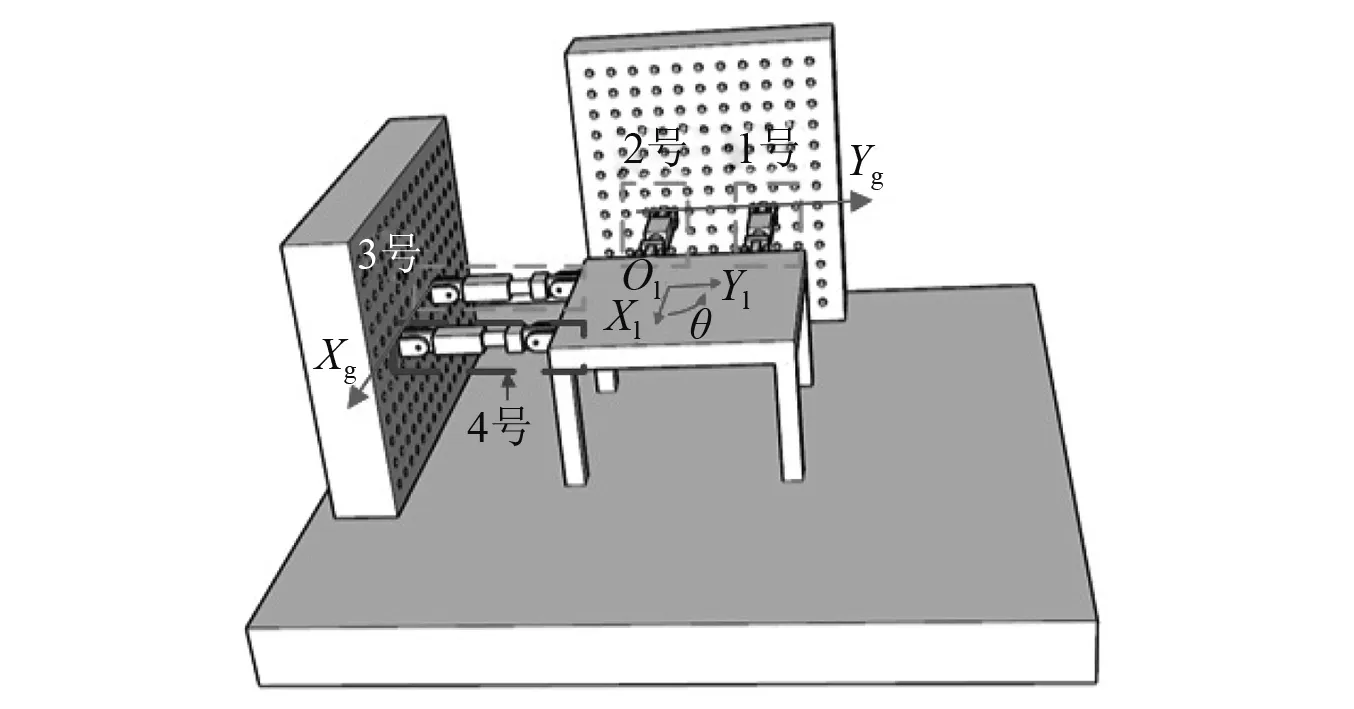
图1 试件及加载设备

1.1 基于平面的运动学分析

为准确分析试件运动性能，需要采用两套坐标系来进行数学描述：第一套坐标系是固定于地面的整体坐标系XgOgYg；第二套坐标系是固定于楼板上且以质心Ol为原点的局部坐标系XlOlYl，整体坐标轴和局部坐标轴始终相互平行。以第i号作动器为例，在作动器未出力之前，作动器与楼板连接点坐标为Ai，作动器出力之后，楼板发生平动和转动。假定楼板先发生绕质心转动，再发生平动，如图2所示。

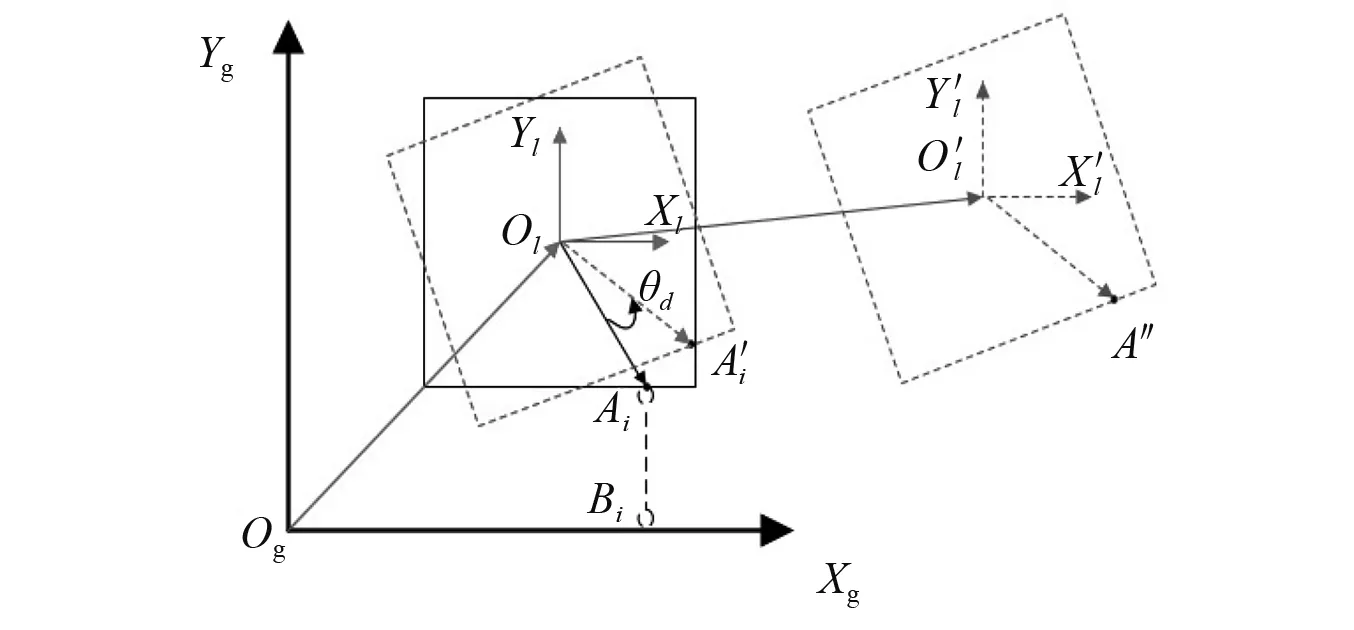
图2 楼板位置变换

因此，可设楼板发生绕质心转动后，Ai变换到A′i，发生平动后，A′i变换到A″i。设质心位移命令记为

d=(xd,yd,θd)T

(1)

在作动器作用之前，已知位移矢量：

则A′存在如下矢量关系

OlA′i=T·OlAi

(2)

OgA′i=OgOl+OlA′i

(3)

由式(2)和式(3)可以得到

(4)

A′iA″i=(xd,yd)T为考虑楼板平动矢量，得到

OgA″=OgA′+A′A″

(5)

由式(4)和式(5)得到

(6)

所以作动器的伸长量可以表示为

Li=‖BiA″i‖2-‖BiAi‖2=
‖OgA″i-OgBi‖2-‖OgAi-OgBi‖2

(7)

式中：OgBi为作动器与反力墙连接点位置矢量； ‖·‖2为2-范数,作动器的伸长量与楼板质心位移之间的函数关系表示为

Li=G(d)

(8)

1.2 基于平面的静力学分析

在楼板平面内三个自由度方向上建立恢复力与作动器出力之间的方程。第i号作动器出力方向的单位向量为

(9)

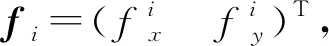
(10)

式中：k1=(1 0)T、k2=(0 1)T分别为整体坐标系XgOgYg的横轴与纵轴的单位矢量。

(11)

整理式(10)、式(11)可以简记为

fvi=Tifi

(12)

若试件的恢复力为R=(rxryrθ)T，则作动器出力值与试件恢复力之间的关系为

(13)

式(13)可以化为矩阵形式[19]

R=AF

(14)

式中：F=[‖f1‖2‖f2‖2… ‖fn‖2]T，

式中：Mi=-e1·k1(yA″i-yol)+e1·k2(xA″i-xol)。

1.3 基于内点法和拉格朗日乘子法的冗余作动器控制方法

式(14)对应三个自由度，但有多于三个的未知量，理论情况下具有无穷多组解，这为优化作动器出力提供了可能。内点法[20]可以利用问题中的约束函数和目标函数构造出新的目标函数，把不等式约束问题的求解转化为求解一系列无约束非线性规划问题。该方法求解形式是从可行区域内部收敛到约束问题边界上的解。

拉格朗日乘子法是一种经典求解条件极值的解析方法，可将所有等式约束的优化模型问题转化为求解无约束极值问题[21]。

本文针对楼板平面内的三自由度控制问题，为使各台作动器出力值相对均匀，以各台作动器出力值平方和最小作为优化目标并考虑作动器的最大出力，以式(15)表示；作动器约束条件以式(14)和式(16)表示

(15)

(16)

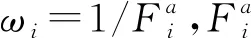
式(14)～式(16)运用内点法和拉格朗日乘子法得到考虑约束条件的目标控制函数为

(17)

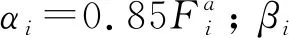
以4台作动器为例，式(17)中对各变量的偏导数为0，即

(18)

为方便理解，将式(18)展开为：

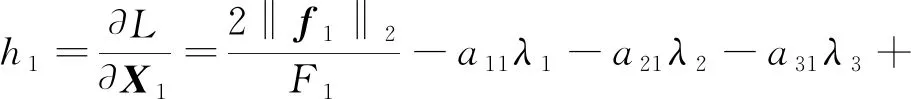
以上aij代表式(14)A中第i行第j列元素，Xi代表X中第i个变量，求解可以采用牛顿迭代方法，本文给出牛顿迭代格式如下

(19)

式(19)中雅可比矩阵J为

2 数值分析

2.1 作动器能力可行域

为检验考虑作动器能力范围的冗余作动器控制方法，现以一个算例来进行数值模拟。已知楼板尺寸为长×宽=2.0 m×2.0 m，仅考虑楼板质心处平面内的三个自由度，设定试件在Xg、Yg方向刚度均为100 kN/mm，转动刚度为100 kNmm/rad。采用4台液压伺服作动器，其初始长度为1 m，最大出力均为2 000 kN，定义4号作动器为冗余作动器，其试验平面图为图3。

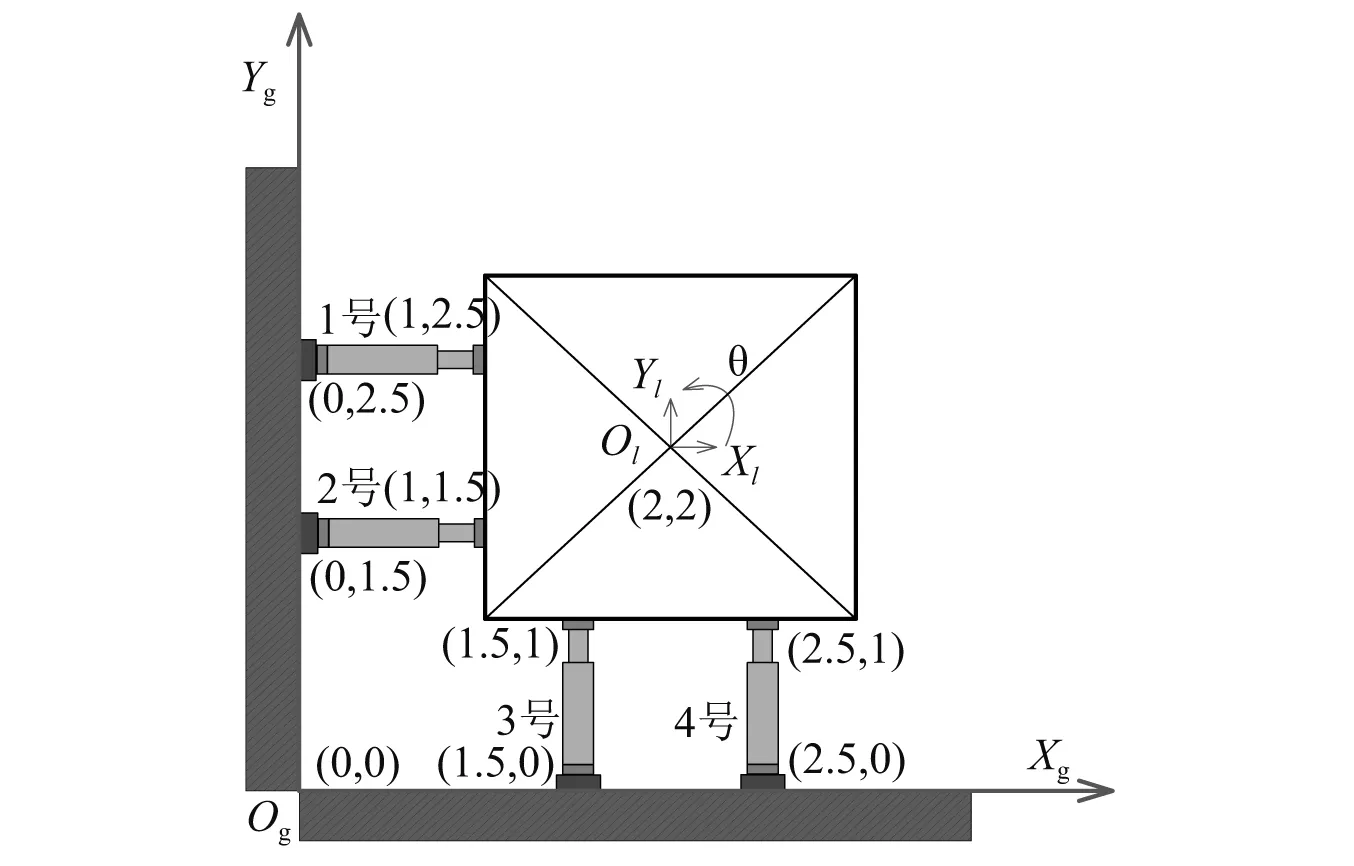
图3 楼板平面位置及作动器编号

采用MATLAB软件模拟，式(17)对各变量的偏导数为0，对于非线性方程组(18)采用式(19)形式进行迭代求解。

加载系统的运动性能由其结构形式和作动器参数所决定。本文将作动器组成的加载系统对结构产生的闭合曲线称之为作动器能力可行域，并将其作为衡量作动器使用和布置以及冗余控制是否合理的重要指标。如果试验预加载位移在作动器能力可行域内，试验能够顺利进行；如果试验预加载位移在作动器能力可行域之外，试验可能导致失败。求解该系统下作动器能力可行域时令惩罚因子为μi=0，流程图如图4所示，试件质心在不同转角θd命令下作动器能力可行域如图5所示。

图4 作动器能力可行域求解过程

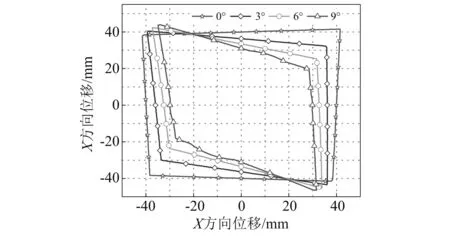
图5 楼板在不同转角命令情况下的作动器能力可行域

结果表明，加载设备对试验对象加载时存在加载极限；考虑试件转动情况在某些情况能够增强加载系统在空间的作用能力，但是多数情况下试件转动会降低其作用能力。在试验之前相关试验人员可根据本节内容验证加载系统能力，为作动器布置形式和型号等方面提供理论依据。

2.2 冗余作动器的控制效果

对于冗余作动器控制方法，为与文献[17]的作动器控制方法相比较，令θd=0，此时更改惩罚因子为μi=10-2，求出两种方法的作动器能力可行域，如图6所示。图中也给出了试件质心位移曲线，选择Δx=0.01 mm将运动轨迹离散，随着试件质心位置变动求解冗余作动器出力结果。冗余作动器的出力值与质心位移在Xg方向的分量之间的关系如图7所示。

图6 楼板质心运动轨迹

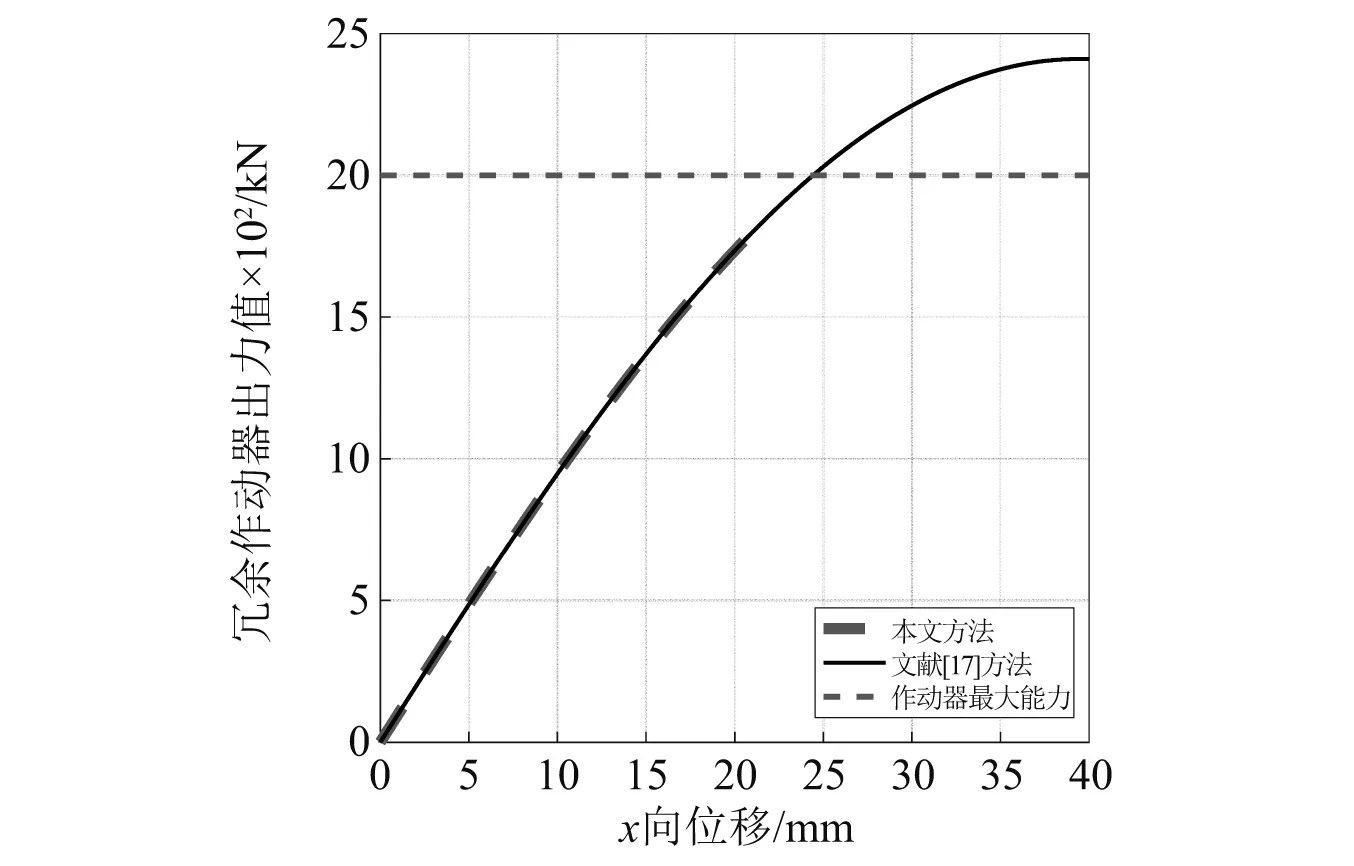
图7 冗余作动器出力结果

该试验结果显示，当位移命令使作动器实际出力值在其作动器能力可行域之内时，两种控制方法效果一致，表明该方法的可行性；当位移命令使作动器实际出力值接近或超过其最大能力时，本文方法不会产生作动器出力命令，从而保证了加载系统和试验人员的安全。另外，因为在目标函数中引入初始控制力αi，所以本文方法可以通过调节该参数来改变作动器能力可行域。

3 虚拟混合试验

3.1 基于Simulink的加载控制系统

为了验证本文提出的冗余作动器控制方法，搭建了采用多台作动器的双向试验加载仿真平台如图8所示。作动器模型采用标准二阶传递函数[22]

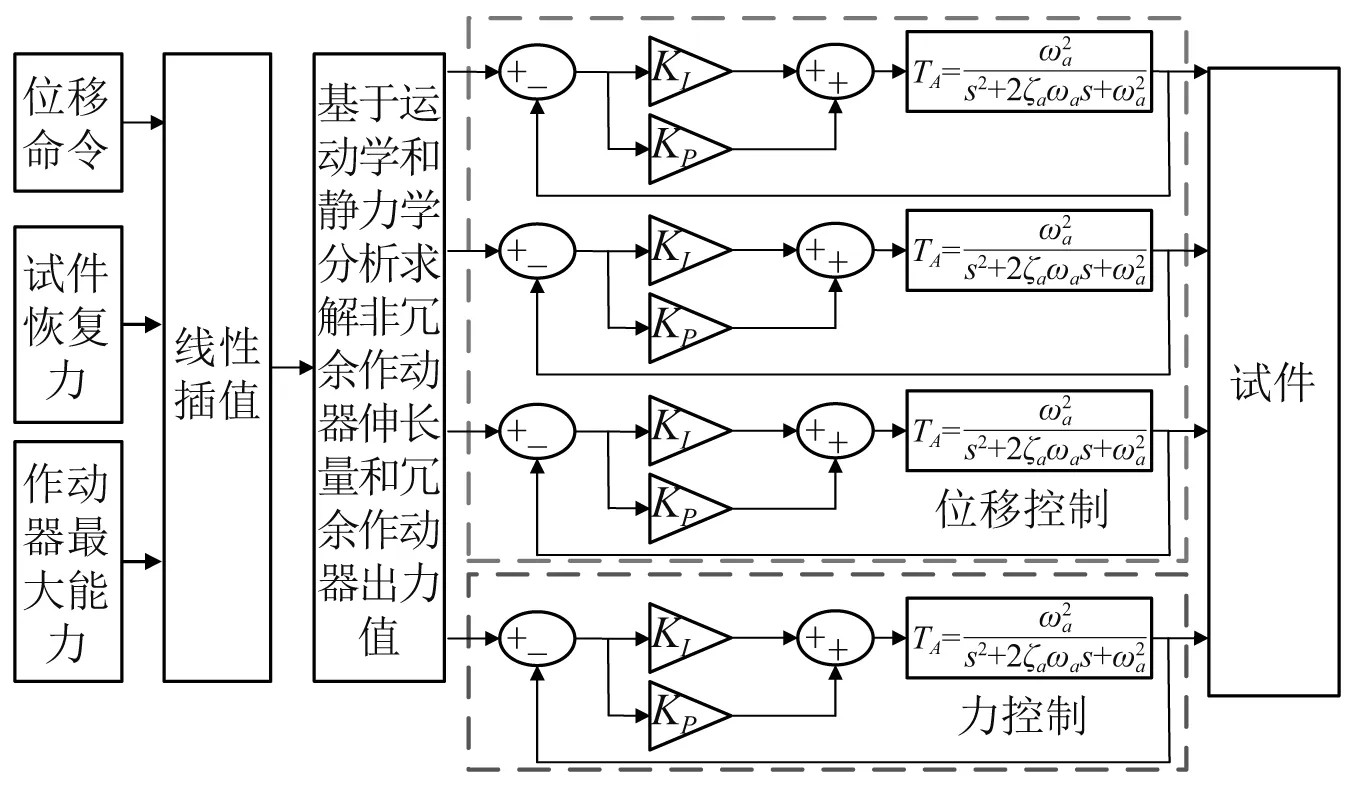
图8 基于Simulink的加载控制系统

(20)

式中： 作动器的等效阻尼比ζa取80%，等效圆频率ωa取300 rad/s。采样时间设定为0.001 s，对单台作动器通过阶跃响应调试其PI参数如图9所示。选取KI=50，KP=0.1。

图9显示该作动器具有时滞τ=0.15 s，因此以上试验加载控制系统不能很好地模拟实时混合试验[23-24]。由于本例为对慢速混合试验[25]的模拟，故不需要考虑时滞问题。为消除时滞对仿真结果的影响，本文对加载目标进行线性插值并给出插值个数：N≥Δτ/Δt-1。

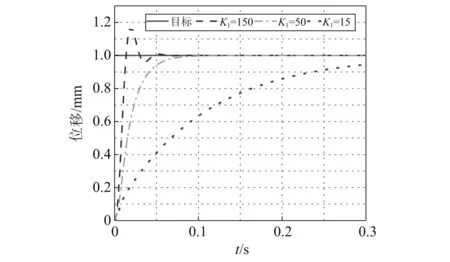
图9 作动器模型的单步阶跃响应

结合MATLAB和Simulink进行加载控制系统的数值仿真，设定一组简单位移命令，其中，频率全为5 Hz，x轴平移振幅为10 mm，y轴平移振幅为20 mm，绕z轴转动振幅为0.01°，由于时滞是0.15 s，N≥14，取N=19。如式(21)所示，系统响应如图10所示。

图10 消除时滞后的系统响应

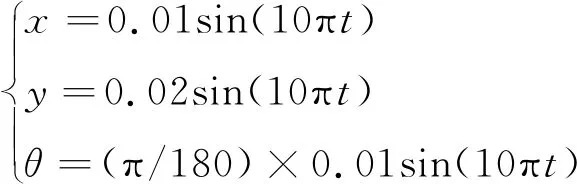
(21)

由图10可知，选择插值点个数N为19个，时滞对仿真结果带来的误差几乎消除。

3.2 冗余系统与非冗余系统的比较

为设立非冗余系统作为对照组，将此系统去掉4号作动器，其他作动器参数保持不变，为比较冗余系统与非冗余系统的工作状态，设定转角为0，其运动参数如式(22)，各台作动器出力值如图11所示。

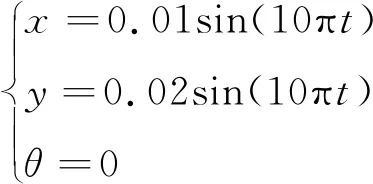
(22)

由图11可知，在1号作动器出力峰值处t=0.01 s时，非冗余系统1号和2号作动器在x向合力为Fx=F1+F2=-500 kN+1 500 kN=1 000 kN，冗余系统1号和2号作动器在x向合力为F′x=F′1+F′2=500 kN+500 kN=1 000 kN；非冗余系统各台作动器出力最大值之和为4 000 kN，而冗余系统各台作动器出力最大值之和为3 000 kN。综上所述，冗余系统不仅能够减小作动器之间产生的内力，而且还可以充分利用小型作动器完成大型试验。

图11 冗余系统与非冗余系统响应

3.3 基于MATLAB和OpenSees & Simulink的虚拟混合试验

为仿真控制系统对试验过程的效果，以在中国建筑技术中心完成的双向混合试验等效结构为试验对象，如图12所示。结构双向跨度均为6.5 m，底层层高为3.9m，二层层高为3.5 m。每层楼板仅考虑平面内的三个自由度，布置4台作动器，其中4号作动器均为冗余作动器，底层布置的4台作动器量程信息为-1 500～1 000 kN，二层布置的4台作动器量程信息为-3 000～2 000 kN。在OpenSees中分别建立数值子结构模型和物理子结构模型，模型将结构质量集中在梁柱结点上，每个结点质量为26 000 kg，梁柱模型采用nonlinearBeamColumn单元，钢材采用Steel02模型，混凝土采用Concrete01模型，材料参数如表1、表2所示。截面等参数信息参见文献[26-27]。

图12 试件及加载设备

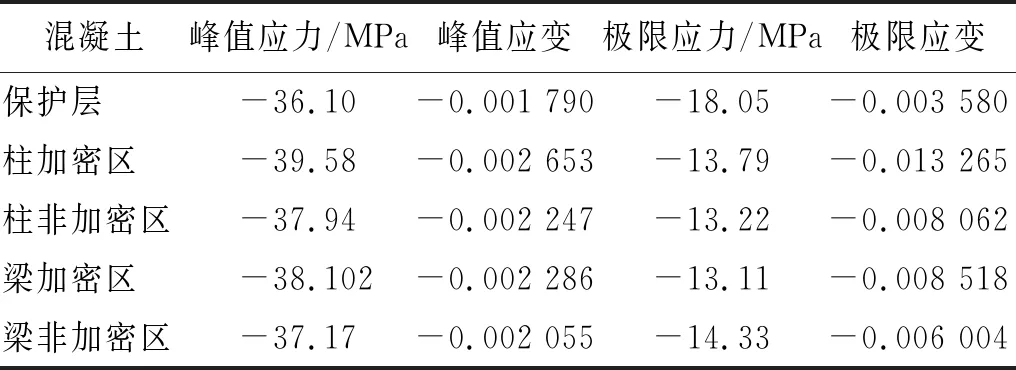
表1 混凝土材料信息

表2 用钢材料信息

对结构输入双向地震动：El Centro 1940(NS)、El Centro 1940(WE)，调节地震加速度峰值：X向为400 gal，Y向为302.86 gal。MATLAB作为协调器，实现与OpenSees和Simulink实时交互，当前步试件恢复力采用结构上一步采集的试件恢复力。具体流程如图13所示，位移实现如图14所示，各台作动器力时程曲线如图15所示。

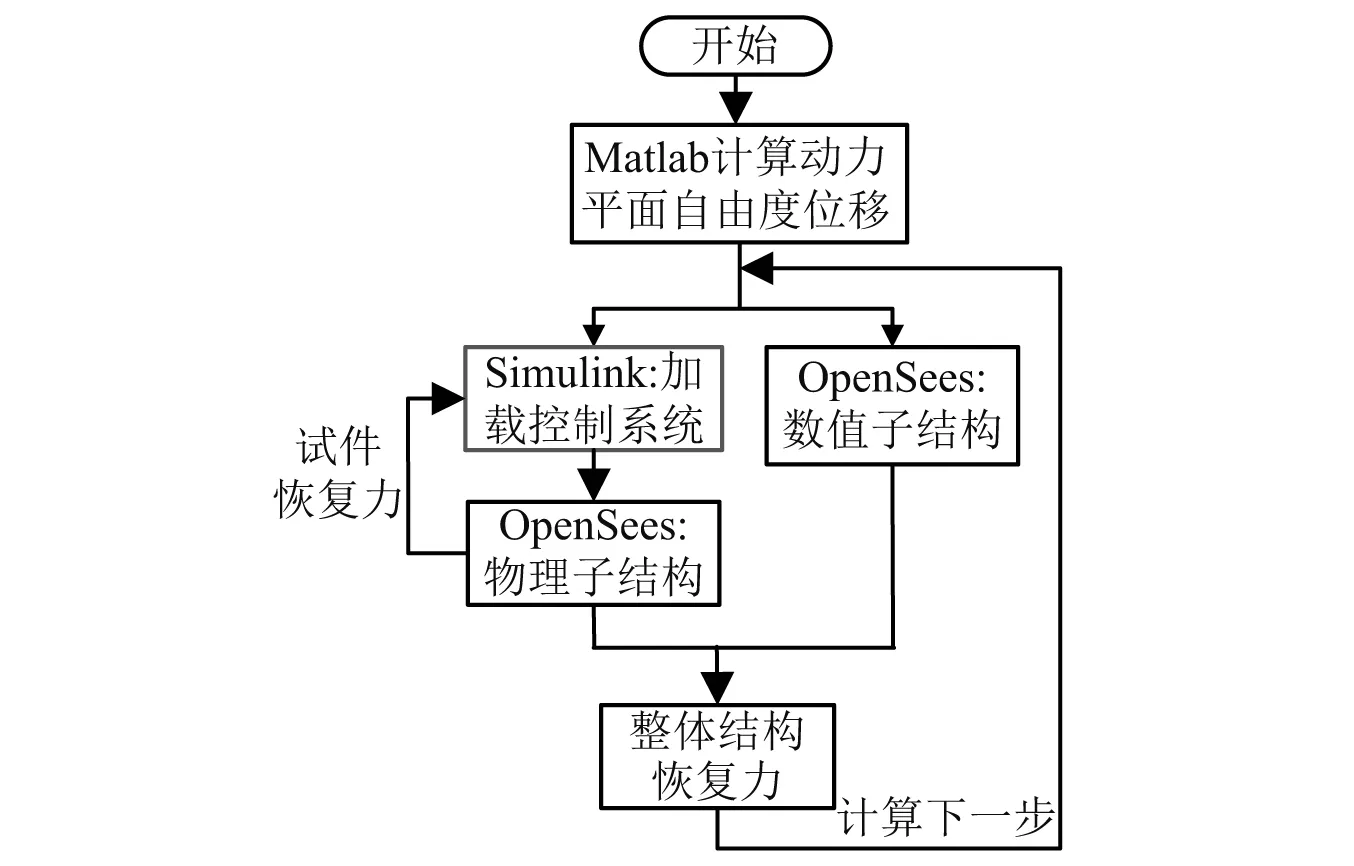
图13 混合试验流程

图14 楼层位移命令与响应

图15 各台作动器力时程曲线

从图13可以看出，加载控制系统能够与位移命令很好地吻合在一起，表明本文提出的冗余控制方法具有很高的精度。从图14可以看出，同层同方向上的两台作动器出力几乎相同，表明本方法可以保证作动器出力均匀，从而充分发挥作动器的加载能力。同时，通过各作动器的出力时程，还可以获得各作动器最大出力值，从而可以为试验人员选择作动器吨位提供支持。

4 结 论

本文针对双向混合试验中的冗余作动器问题，提出了基于内点法和拉格朗日乘子法的冗余作动器控制方法和作动器能力可行域计算方法，搭建了基于Simulink冗余加载控制仿真系统，并通过双层双向结构的虚拟混合试验加以验证，主要结论如下：

(1) 提出了考虑作动器出力边界的冗余作动器控制方法，数值模拟表明该方法可以避免作动器出力超界，同时还能充分考虑作动器的加载能力。

(2) 提出作动器能力可行域的计算方法，指出作动器能力可行域不仅与作动器的布置位置和型号有关，还与试件恢复力和实际转角有关。本方法可为试验人员在布置和选择作动器时提供参考。

(3) 搭建了基于Simulink的冗余加载控制仿真系统，分析了冗余控制系统和非冗余控制系统的工作状态。结果表明冗余控制系统消除了系统内力，降低了对作动器最大出力的要求，并且减小了系统总出力值。

(4) 以中国建筑技术中心完成的双层双向混合试验为原型，开展了双向虚拟混合试验，结果表明所提冗余控制方法控制精度较高，还能保证各台作动器出力均匀，充分发挥作动器的加载能力。