积分在大学物理中的应用探究
袁朝圣++徐英
摘要:本文结合定积分的定义,利用“大化小,常带变,近似和,求极限”的方法解决了水的侧压力问题,进一步认识了积分的本质特点为求和、求极限。以具体的物理问题为例,给出了定积分、曲线积分和曲面积分解决物理问题的本质方法是“微元分析法”,总结出了“微元分析法”解决物理问题的一般步骤。
关键词:积分;物理;微元分析法
中图分类号:G642.0 文献标志码:A 文章编号:1674-9324(2014)52-0139-03
大学物理中的许多问题都要用微积分来解决,如水压力、变力沿直线或曲线做功、物体的质心、刚体的转动惯量以及E通量等。事实上,微分可以理解为对整体的无限分割,使得局部无限的小,积分则可以理解为对无限个小微元的求和[1]。概括地说,微分是分割的过程,积分则是一个求和、求极限的过程。本文以具体的物理问题为例,分析了积分方法在大学物理中的应用。为了深化对积分概念的理解,本文以水的侧向压力为例,采用“大化小,常带变,近似和,求极限”的思想进行分析,讨论了积分的本质思想及其物理意义,并利用“微元分析法”[2]给出了该问题的简单解法。另外,本文通过对变力沿曲线做功问题的求解和对阿基米德原理的证明,给出了曲线积分、曲面积分解决物理问题的本质方法仍是“微元分析法”。
一、积分在大学物理中的应用
根据积分的定义[2,3],我们可以得出,凡是可以通过“大化小,常带变,近似和,求极限”这四步来解决的物理量均可用积分来求解,即可利用“微元分析法”来解决物理问题。本文以具体的问题为例,来分析积分在物理问题中的应用。
(一)定积分的应用——水的侧压力问题
例1 一个横放着的圆柱形水桶,桶内盛有半桶水,设桶的底半径为R,水的密度为ρ,计算桶的一个端面上所受的压力。[2]
为了深化对积分概念的理解,本文首先根据“大化小,常带变,近似和,求极限”的思想求解该题。
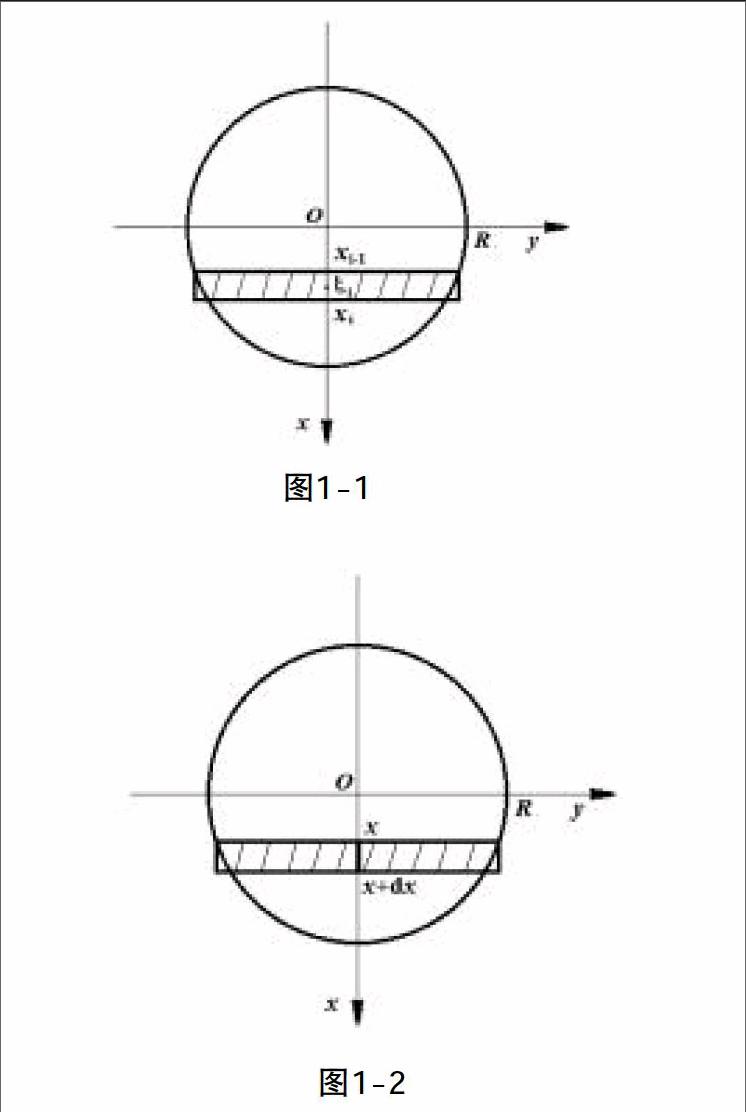
解:桶的一个端面是圆片,我们要计算的是当水平面通过圆心时,铅直放置的一个半圆片的一侧所受到的水压力。在这个圆片上,如图1-1,在取过圆心且铅直向下的直线为x轴,过圆心的水平线为y轴,则半圆片所在圆的方程为x2+y2=R2,记y=f(x)=■.
第一步:“大化小”,把半圆片分成n个小窄条,即把区间[0,R]分成n个小区间[x0,x1],[x1,x2],…[xn-1,xn],其中x0=0,xn=R.每个小窄条一侧所受的水压力的和即为半圆片的一侧所受的水压力。
第二步:“常带变”,把第i个小窄条(i=1,2,3,…,n)近似地看成矩形窄条,如图1-1,该矩形的高为Δxi=xi-xi-1,任取一点ξi∈[xn-1,xn],让2f(ξi)作为该矩形的底,即小矩形的底为2■,则第i个小窄条所受的侧压力Pi的近似值可表示为:
Pi≈ρgξi2■Δxi,i=1,2,3,…,n
第三步:“近似和”,由上面的讨论可得半圆片一侧所受的侧压力P的近似值为:P≈∑■■ρgξi2■Δxi.
第四步:“取极限”,Δxi越小,近似和也就越接近于精确值P,当Δxi无限小时,即Δxi趋于零时,近似和就是精确值P.
取λ=max{Δx1,Δx2,…,Δxn},则半圆形圆片一侧所受的侧压力为:
P=■■ρgξi2■Δxi.
根据定积分的定义,上述极限即为函数f(x)=ρgx2■在区间[0,R]上的定积分,即
P=■■ρgξi2■Δxi=■ρgx2■dx.
综上,我们得到了桶的一个端面上所受的压力为
■ρgx2■dx=2ρg■x■dx=■R3.
通过对该题的求解,我们可以得到:当所求物理量满足一定条件(该物理量可以根据“大化小,常带变,近似和,求极限”的思想来求解)时,那么该物理量可以表示为一个函数在某区间上的定积分。事实上,我们可以把定积分简单地理解为求和、求极限。
对于例1,可以利用“微元分析法”,得出该题的简单求解方法,具体过程如下:
解:对于上面所建立的坐标系,我们取为积分变量,且x∈[0,R]在该区间上取任一小区间[x,x+dx],如图1-2,用点x处的压强来近似地表示该小区间上任一处的压强,因此相应于该小区间的窄条上各处的压强可近似地表示为ρgx,该窄条的面积可近似地表示为:
2ydx=2■dx.
因此该窄条一侧所受的水压力的近似值,即桶的一个端面上所受水压力的微元表达式为:
dp=2ρgx■dx
因此,所求的压力为:
P=■2ρgx■dx=■R3.
(二)曲线积分的应用——变力沿曲线做功问题
例2 有一质量为4kg的质点,在力F=(2xy,3x2)(SI单位)的作用下,沿曲线x2=9y从点(0,0)运动到(3,1),求力F在质点运动过程中所做的功。[4]
讨论:该题为变力沿曲线做功问题,且所求的量可以通过“大化小,常带变,近似和,求极限”来解决,因此可以利用“微元分析法”来求解。由于质点的运动路径为曲线弧,故选取微元为弧元素ds.该题的具体求解过程如下:
解:对于曲线弧x2=9y,x∈[0,3],在该弧上取弧元素ds,P(x,y)为ds上的任一点,P点处沿x轴增加方向的切向量的方向余弦为:cosα,cosβ.
可以得到:力F在x轴、y轴方向上的分量所做功的微元表达式分别为:2xycosβds,3x2cosαds.
所以所求功为:
W=■2xycosβds+■3x2cosαds=
■2xydx+3x2dy=18J.
该题是曲线积分的一个典型的应用,涉及到了两类曲线积分的概念及其联系。事实上,此题也可以直接在x轴、y轴分别取微元dx、dy,进而直接应用对坐标的曲线积分,得到所求功的表达式为:endprint
■2xydx+3x2dy.
(三)曲面积分的应用——阿基米德原理的证明
阿基米德原理:浸没在液体中的物体所受的浮力等于该物体排开的同体积液体的重力,浮力的方向铅直向上。[4]
例3 证明阿基米德原理。
对于该原理的证明,文献[4]给出了很完整的证明过程。本文利用高斯公式,参考文献[5]中的解题思想,严格按照“微元分析法”解决物理问题的步骤,给出该原理的另一证明思路。
证明:建立坐标系,取液面为xoy坐标面,铅直向上的方向为z轴,由于物体表面各点处均有压强,因此我们选取积分元为曲面元dS,积分区域为物体表面∑,在dS上取点M(x,y,z),由于z轴方向铅直向上,所以z≤0.物体表面在该点处所受的压强大小为-ρgz.
设∑在M处的外法线向量的方向余弦为:cosα,cosβ,cosγ.则dS所受压力在x轴、y轴、z轴上的分量的微元表达式分别为:-ρgzcosαdS,-ρgzcosβdS,-ρgzcosγdS.
记物体所所受液体的压力在x轴、y轴、z轴上的分量分别为:Fx,Fy,Fz.
于是可得:Fx=■-ρgzcosαdS;Fy=■-ρgzcosβdS;Fz=■-ρgzcosγdS.
(其中,Ω为物体所占有的空间区域,V为物体的体积。)
利用高斯公式可得结果:
Fx=■■dxdydz=0;
Fy=■dxdydz=0;
Fz=■■dxdydz=-ρgV
事实上,物体左右两侧受液体水平方向的压力等值、反向、共线,因此,物体所受水平方向上的合力为零。因此物体所受的合力为F=-ρgV.该力大小等于物体的重力,方向铅直向上。
在该题的证明过程中,我们可以把坐标原点选取在xoy坐标面的任一处,因此在建立坐标系时无须确定坐标原点。曲面积分的求解一般是转化成定积分来计算,但在该题中,积分曲面不能够具体地表示出来,因此曲面积分无法转化成定积分。但可以利用高斯公式把曲面积分转化成三重积分,转化后的三重积分的被积函数是1,根据三重积分的定义[3],可得该三重积分的值恰好是积分区域的体积。
二、结论
本文以具体的物理问题为例,分析了积分方法在大学物理中的应用。当所求物理量可以根据“大化小,常带变,近似和,求极限”的思想来解决时,那么该物理量可以简单地表示为一积分表达式,即该物理量可以利用微元分析法来求解。事实上,大学物理中的很多公式都是抽象的数学公式的具体化;而数学公式大都是抽掉了具体物理意义的数量关系。因此,在解决实际物理问题时,必须在掌握数学知识的同时明确物理概念,将数学与物理紧密地联系起来。
另外,本文还总结了利用微元分析法求解物理问题的一般步骤:(1)建立方便的坐标系。对于一个具体的物理问题,建立坐标系的原则是使得计算过程较简便。(2)确定积分区域。对于不同的问题,积分区域可能是:数轴上的区间;平面域;空间域;曲线弧;曲面域。(3)写出微元表达式。把积分区域分割为许多小区域,写出小区域上待求物理量的近似值。(4)写出积分表达式并求解。
参考文献:
[1]梁小佳.微积分在大学物理中的应用探究[J].甘肃高师学报,2010,15(2):78-80.
[2]同济大学数学系.高等数学(上册)[M].第6版.北京:高等教育出版社,2007.
[3]同济大学数学系.高等数学(下册)[M].第6版.北京:高等教育出版社,2007.
[4]毛骏健,顾牡.大学物理(上册)[M].北京:高等教育出版社,2006.
[5]同济大学数学系.高等数学习题全解指南(下册)[M].第6版.北京:高等教育出版社,2007.endprint

