基于可信位置排序的咬尾卷积码译码算法

王晓涛 刘振华

1 引言

卷积码在编码时其编码器可以用已知比特来初始化，也可以用信息比特来初始化。对于寄存器长度为v的卷积码编码器，当采用信息比特的最后v位来初始化编码器时，编码结束时编码器的状态和其初始状态是相同的，同时码字对应的格形图呈咬尾状态[1,2]。我们称这种方式得到的码字为咬尾卷积码（Tail-Biting Convolutional Codes, TBCC），其对应的格形图为咬尾格形图。

采用咬尾方式编码可以消除用已知比特初始化编码器带来的码率损失[35]-，这种损失对于短码来说显得更为严重，比如对于生成多项式为{354, 237}（8进制），信息序列长度为32的卷积码来说，如果不采用咬尾编码其有效码率损失会达到20%。因此咬尾卷积码作为一种高效的短码编码方式被广泛用于各种通信系统中作为控制信道和广播信道的编码方案，如在增强型数据速率 GSM 演进技术（Enhanced Data rate for GSM Evolution, EDGE）[6]和 3GPP 长期演进项目（Long Term Evolution,LTE）[7]等通信系统。

由于咬尾卷积码的编码器采用信息序列进行初始化，因此其对应的咬尾格形图在起始位置有2v个起始状态，这种结构给译码器的设计带来了困难[812]-。目前咬尾卷积码的译码算法主要有3大类：基于循环Viterbi算法（Circular Viterbi Algorithm,CVA）的译码算法，如WAVA和TD-CVA等[1,13]；基于 Viterbi算法和启发式搜索的混合式译码（Viterbi-Heuristic, VH）[14]；和基于双向搜索的有效译码算法（Bidirectional Efficient Algorithm for Searching code Trees, BEAST）[15]。BEAST 算法工作时需要将咬尾格形图转化成传统格形图，且需要保存整个格形图的结构信息，这将消耗大量的存储空间。比如对于（24,12）的Golay码来说，其传统格形图的中间位置处的状态数高达512个[15]，而其具有最低状态复杂度的咬尾格形图在每个位置处的状态数只有16个[11]。VH算法分为两个译码阶段，在第1阶段Viterbi算法将咬尾格形图上所有位置处到达每个状态的幸存路径的度量值保存下来，利用这些信息进行启发式搜索。VH算法的两个译码步骤基于两种完全不同的搜索算法，不仅需要保存大量的中间信息，同时译码器实现复杂度高，不利于实际应用。

CVA是一种完全基于Viterbi的译码算法，通过在咬尾格形图多次迭代来寻找最优咬尾路径及其对应的码字。传统的基于CVA的译码算法没有考虑译码过程中存在的循环陷阱，这导致译码器在译码结束时可能无法收敛到最优咬尾路径，因此是一种次优译码算法，如WAVA和ET-CVA等。TD-CVA从循环陷阱出发，通过在迭代过程中对非最大似然状态的排除，使得译码器能最终收敛到全局最优咬尾路径。

本文利用咬尾格形图的循环性，提出了一种基于CVA的最大似然译码算法。新算法首先根据接收到的似然比信息来确定可靠性最高的起始位置，然后从该起始位置处开始译码。这样经过几个分支的搜索以后，幸存路径的起始状态会收敛到更少的幸存状态上。相对于已有的算法，本文算法具有更快的收敛速度，译码效率得到进一步提高。

本文结构如下，第2节介绍新算法的设计原理，并通过例子给出算法说明，同时对算法的最优性进行证明；第3节给出算法性能仿真验证；第4节总结全文。

2 算法描述

2.1 变量定义

如图 1所示的咬尾格形图T是生成多项式为{7,5}、信息序列长度为 L = 8 的TBCC对应的咬尾格形图。格形图T中位置l处的状态集合记为 Sl，0≤l≤L（S0= SL）。对于咬尾卷积码来说其咬尾格形图是规则的[12]，即有 Si= Sj, 0 ≤ i , j ≤ L 。格形图T中任意位置l处的状图s都有其对应的咬尾格形子图，记为Tsub（s）。图1中实线所示为位置l=2处的状态s=01的咬尾格形子图。Tsub（s）上所有完整路径都是咬尾路径，整个咬尾格形图T是由位置l处所有状态的咬尾格形图的并集组成[12]，即有

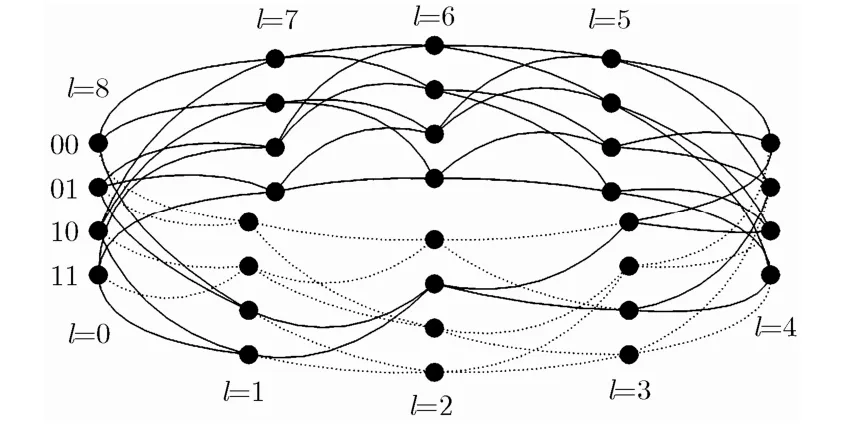
图1 生成多项式为{7,5}的咬尾卷积码格形图

在译码开始的时候，对接收到的软信息进行处理以选择可靠性最高的位置lopt作为译码的起始位置。设信息序列长度为L的TBCC的码率为 b/ c，编码以后的码字为∈ {0,1}，其中0≤l≤L,0≤j≤c-1。设码字经过BPSK调制得到映射后的符号为：= （ 1 -），不失一般性令 Es为1。经过双边噪声功率谱密度为 N0/2的高斯白噪声（Additive White Gaussian Noise, AWGN）信道后，对应接收到的符号为，计算得到似然比信息=/。定义l 的计算方式为opt

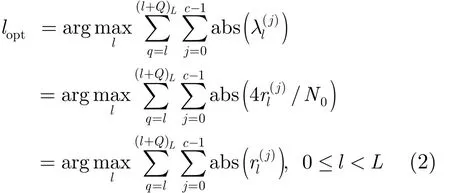
式 中 （l+ Q ）L= （ l+ Q ） mod L ， 其 中Q是待 确 定 的量，在具体应用中将根据不同的码字选择合适的值。

2.2 算法说明

由于CVA的译码过程是迭代的，即在第i次迭代中每个状态的初始度量值是用第 i - 1次迭代得到的幸存路径的度量值来初始化的，因此每次迭代都会得到不同的幸存路径及其路径度量值[1]。第i次迭代中，起始于状态s，结束于状态s'的幸存路径记为 Pi（ s, s'） ，其中 s , s '∈, Pi（ s, s'） 对应的路径累积度量值记为 Mi（ s, s'）。如果咬尾格形图T上的幸存路径的起始状态和终止状态相同，即 s = s '（ ∈ Slopt） ，则路径Pi（ s, s）为咬尾路径。T（s）是由所有从状态subs起始并结束到状态s的咬尾路径的集合构成，记Tsub（s）上对应于接收序列度量值最大的咬尾路径为s, s）：

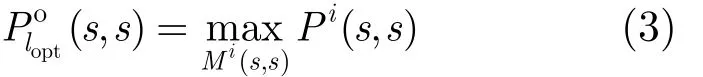
其中 s ∈Slopt, i≥1。

算法的步骤描述如下：

步骤1 根据式（2）计算最佳译码起始位置lopt，初始化迭代次数 i = 0 ，令= S ； lopt

lopt有循环陷阱产生：

（a）有循环陷阱：找到具有最大路径度量值Mi（ s, s'） 的幸存路径 Pi（ s, s'） ，在T（s） 上执行一

sub次 Viterbi算法得到（s, s），将s从中删除；同时若（s, s）＞，更新；返回步骤2。

（b）无循环陷阱：返回步骤2。

步骤4 令 Po=，输出 Po作为最终译码结果，译码结束。

2.3 最优性证明

由文献[1]可知，通过对循环陷阱的控制，译码算法最终会收敛到，而是译码器从位置lopt处开始译码得到的最大似然咬尾路径，因此证明算法的最优性就是证明译码结果与起始位置无关。

定理 1 译码算法在咬尾格形图上得到的最大似然咬尾路径与译码起始位置相独立，即有 Po=。

因为（,）P s s是咬尾路径，由咬尾路径定义可知该路径在咬尾格形图上起始和结束于同一个状态，且任意位置l处的状态集合lS中有且仅有一个状态在咬尾路径上（非咬尾路径在起始位置处不满足此条件）。设（,）P s s经过optlS中的状态s'，则有

可见P（ s, s）是咬尾格形子图Tsub（s'）上的咬尾路径，设Tsub（s'）上的最优咬尾路径为（s',s'），且其路径度量值为（s',s'），从而有

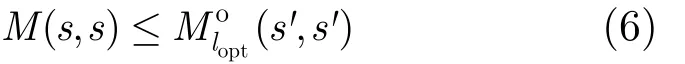
由式（6），式（7）两式可知：

可见式（8）与假设条件式（4）相矛盾，即译码结束时咬尾格形图上不存在任何咬尾路径其度量值大于，译码过程与译码起始位置无关，中保存的即为全局最优咬尾路径，所以有 Po=证毕

3 仿真验证

本节通过两个实验来验证本文算法的有效性，为引用方便，将本文算法记为NCVA（New CVA）。此处选用两种经典算法进行性能比较，WAVA算法和VH算法，这是因为WAVA是咬尾格形图上基于CVA的经典译码算法，而VH算法是咬尾格形图上基于启发式搜索的经典算法。编码以后的比特通过QPSK映射后经过 AWGN信道，接收端接收到信息序列以后分别采用上述3种译码算法进行译码，译码过程中每个译码块的平均访问状态数作为衡量译码复杂度的标准。

在第1个实验中，我们选用LTE中用于控制信道编码的咬尾卷积码码字（120, 40）进行实验，该咬尾卷积码生成多项式为（133, 171, 165）（8进制），编码器寄存器长度为 6v= 。仿真结果如图2所示。将WAVA 性能和 NCVA性能比较可见：由于循环陷阱控制的添加，以及选择可信度更高的译码起始位置，能够极大的提高译码效率；VH算法的性能和NCVA的性能比较可以发现，在信噪比从低到高变化的范围内NCVA都可以达到更高的译码效率。随着信噪比的升高，NCVA从任何地方开始译码都可以得到相同的译码复杂度，即执行一次迭代即可得到最优解；同时VH算法也只需要执行一次Viterbi算法即可得到最优解。因此，NCVA和VH算法的译码复杂度最终收敛到一起，为2vL= 2 560，这和仿真结果相吻合。

表 1中给出了几种不同译码算法的误码率性能。由于VH算法，TD-CVA, NCVA是最优译码算法，因此它们有相同的误码率性能，而WAVA是次优译码算法，因此 WAVA算法的性能要略差于NCVA算法。

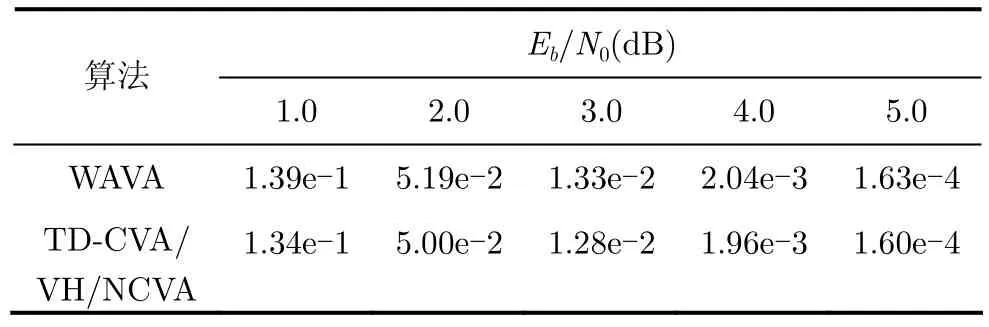
表1 不同译码算法对（120,40）咬尾卷积码译码的误码率性能

和 TD-CVA[1]相比，本文算法利用了可信位置排序来改进算法的收敛速度。为了验证可信位置排序对算法收敛速度的改进，表2中给出NCVA在不同Q值下的译码复杂度和 TD-CVA算法的译码复杂度详细对比列表。通过对比可以发现以下两点规律：

（1）由于可信位置的选择，NCVA 可以比 TDCVA获得更快的收敛速度；

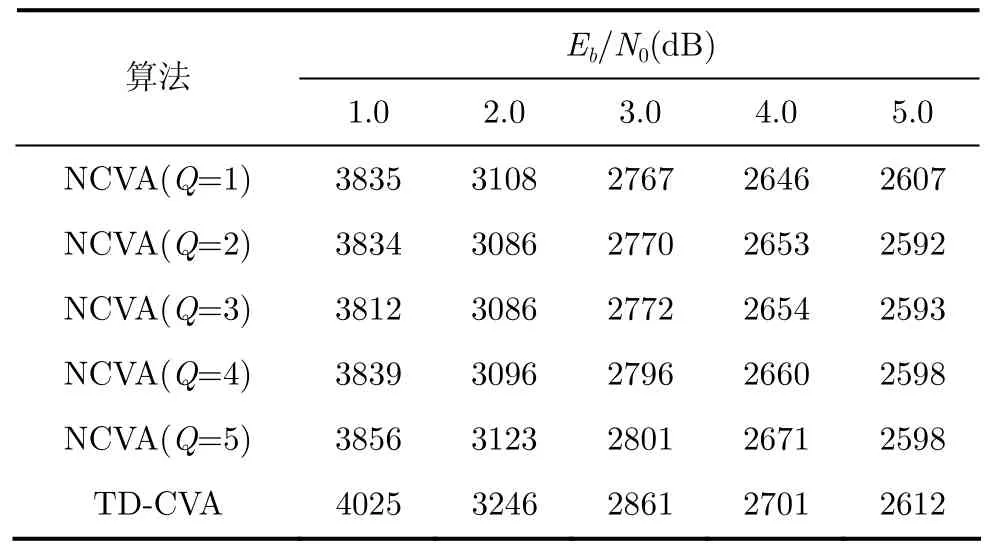
表2 NCVA与TD-CVA算法复杂度对比

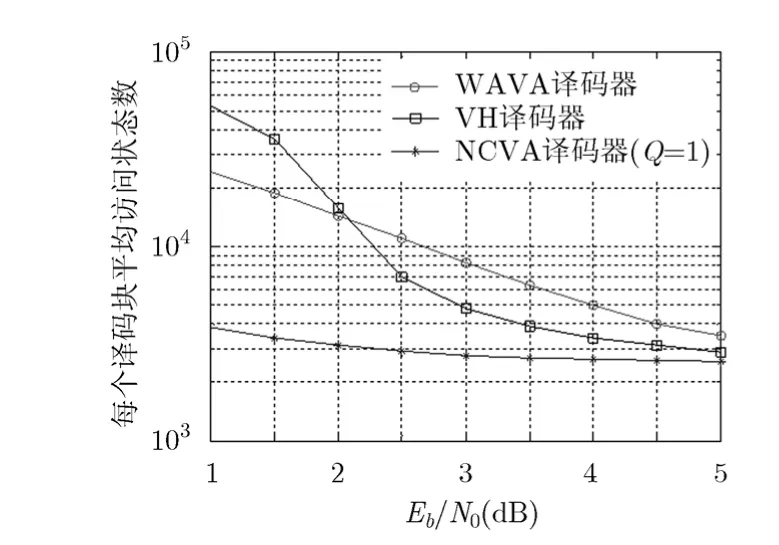
图2 不同译码算法对（120,40）咬尾卷积码的译码性能比较

（2）当Q值越小时，可靠度的作用越明显；由于接收序列服从正态分布，因此当Q值越大时，由式（2）计算得到的每个位置的可靠度越接近；极限情况是Q为接收序列的长度，此时每个位置的可靠度完全一样，那么译码从头开始，复杂度与TD-CVA相同。

综合以上考虑，实际中选取 2Q≤ 。

在第 2个实验中，我们选用（24,12）Golay码为例。Golay码的16状态咬尾格形图状态复杂度低，但是该咬尾格形图是周期为4的咬尾格形图，整个格形图分为3段，长度为12。这种格形图在每个时刻的路径输出不同，不利于译码器的实现，本文选用其64状态咬尾格形图表示，该格形图可以由生成多项式{103, 166}得到[1]。图3中给出了不同译码算法对（24,12）Golay码译码复杂度比较，可以得到和第1个实验相同的结论。

表3中给出了几种算法的误块率性能，可见在信噪比比较高，即 Eb/N0≥ 3 dB 时，次优译码算法WAVA的性能和NCVA性能接近。

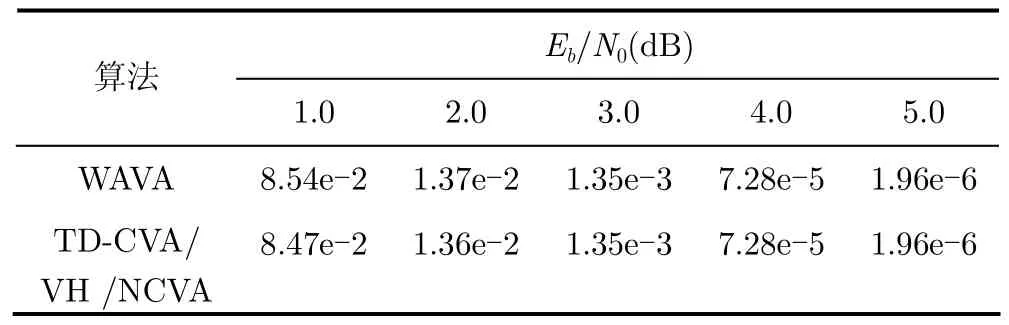
表3 不同译码算法对（24,12）Golay码译码的误码率性能

4 结束语

咬尾格形图具有循环性，在咬尾格形图上的译码过程可以从任意位置开始，最终得到的最大似然译码结果都是相同的。文中以定理的形式证明了这个结论，从任何位置开始译码得到的最优咬尾路径都是全局最优咬尾路径。本文中提出的译码器利用咬尾格形图的循环性，用接收到的信道输出序列先计算一个可信度最高的译码起始位置。从该位置开始译码可以发现译码器能够更快地收敛到最优解，最后的仿真结果也证明了算法有效性。

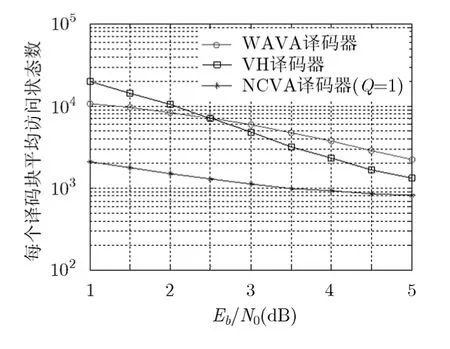
图3 不同译码算法对（24,12）Golay码译码性能比较

[1] Wang Xiao-tao, Qian Hua, Xiang Wei-dong, et al.. An efficient ML decoder for tail-biting codes based on circular trap detection[J]. IEEE Transactions on Communications,2013, 61（4）: 1212-1221.

[2] Gluesing-Luerssen H and Forney G D. Local irreducibility of tail-biting trellises[J]. IEEE Transactions on Information Theory, 2013, 59（10）: 6597-6610.

[3] 王晓涛, 钱骅, 徐景, 等. 基于陷阱检测的咬尾卷积码译码算法[J]. 电子与信息学报, 2011, 33（10）: 2300-2305.Wang Xiao-tao, Qian Hua, Xu Jing, et al.. Trap detection based decoding algorithm for tail-biting convolutional codes[J]. Journal of Electronics & Information Technology, 2011,33（10）: 2300-2305.

[4] 王晓涛, 钱骅, 康凯. 基于 Viterbi-双向搜索的咬尾码最大似然译码算法[J]. 电子与信息学报, 2013, 35（5）: 1017-1022.Wang X T, Qian H, and Kang K. Viterbi-bidirectional searching based ML decoding algorithm for tail-biting codes[J]. Journal of Electronics & Information Technology, 2013,35（5）: 1017-1022.

[5] Wu T Y, Chen P N, Pai H T, et al.. Reliability-based decoding for convolutional tail-biting codes[C]. IEEE Vehicular Technology Conference, Taibei, 2010: 1-4.

[6] 3GPP TS. 45.003-3rd generation partnership project;technical specification group GSM/EDGE radio access network; channel coding （release 9）[S]. 2009.

[7] 3GPP TS. 36.212-3rd generation partnership project;technical specification group radio access network; evolved universal terrestrial radio access （E-UTRA）; multiplexing and channel coding （release 8）[S]. 2009.

[8] Williamson A R, Marshall M J, and Wesel R D.Reliability-output decoding of tail-biting convolutional codes[J]. IEEE Transactions on Communications, 2014, 62（6）:1768-1778.

[9] Bin Khalid F, Masud S, and Uppal M. Design and implementation of an ML decoder for tail-biting convolutional codes[C]. IEEE International Symposium on Circuits and Systems, Beijing, 2013: 285-288.

[10] Zhu L, Jiang M, and Wu C. An improved decoding of tail-biting convolutional codes for LTE systems[C]. 2013 International Conference on Wireless Communications &Signal Processing, Hangzhou, 2013: 1-4.

[11] Calderbank A, Forney G Jr, and Vardy A. Minimal tail-biting trellises: the Golay code and more[J]. IEEE Transactions on Information Theory, 1999, 45（5）: 1435-1455.

[12] Wang X T, Qian H, Kang K, et al.. A low-complexity maximum likelihood decoder for tail-biting trellis[J].EURASIP Journal on Wireless Communications and Networking, 2013, 130（1）: 1-11.

[13] Shao R Y, Lin S, and Fossorier M P C. Two decoding algorithms for tailbiting codes[J]. IEEE Transactions on Communications, 2003, 51（10）: 1658-1665.

[14] Pai H T, Han Y, Wu T, et al.. Low-complexity ML decoding for convolutional tail-biting codes[J]. IEEE Communications Letters, 2008, 12（12）: 883-885.

[15] Bocharova I, Johannesson R, Kudryashov B, et al.. BEAST decoding for block codes[J]. European Transactions on Telecommunications, 2004, 15（1）: 297-305.