多抽头延迟设置与幅相误差对全双工射频自干扰消除的影响
吴 飞 马万治 邵士海 唐友喜
1 引言
同时同频全双工(Co-frequency and Co-time Full Duplex, CCFD)在同时工作的收发通道上使用相同的频谱资源,从而突破了传统的频分双工(Frequency Division Duplexing, FDD)和时分双工(Time Division Duplexing, TDD)模式,频谱效率最大可以提升一倍[14]-,这使得无线通信的上下行频谱资源,可以完全独立进行规划。随着无线通信技术的快速发展,频谱资源越来越稀缺,同频全双工具有成倍提高信道容量的能力,具有显著的理论研究及应用价值,近几年来,得到了业界的广泛关注,成为新的研究热点[57]-。
同时同频全双工在应用中存在自干扰的问题,本地发射的信号与远端设备发送的信号在频谱上重叠,会对接收信号形成自干扰。需要进行自干扰抵消,理论上可以通过天线隔离[8,9]、射频对消[10]和数字对消实现。天线隔离与射频对消在接收信号进入ADC采样量化前实施,数字对消在ADC后的数字域上实施。为了防止过强的自干扰信号对 ADC造成阻塞,进入 ADC之前接收信号干信比必须降低到一定水平,因此,在同时同频全双工系统中,需要进行射频自干扰抑制。
射频对消可以分为直接射频耦合对消和数字辅助射频对消,并且已经得到了工程验证[11]。直接射频耦合对消的典型方法如文献[12]和文献[8,13]。文献[8,13]采样部分本地发送射频信号,通过调节此采样信号的相位和幅度,在2.4 GHz频段和530 MHz频段验证了射频对消的可行性;文献[12]则采用反相和同相两条支路来产生自干扰对消信号,通过调节两条支路的衰减大小,在2.4 GHz频段试验验证射频对消方案。文献[8,12,13]采用传统的单抽头和双抽头射频干扰抑制方案,为了提高多径自干扰信道下射频自干扰抑制效果,文献[10]提出了射频自干扰抑制的多抽头方案,并进行了相应实验。文献[10]中提出的多抽头方案中,延迟样式以及幅度和相位控制误差对射频自干扰抵消性能的影响,还没有文献对其进行相关研究。本文针对此问题,采用直接射频耦合对消方法,分析了多抽头方案的射频对消机理,推导了多径条件下多抽头方案中抽头延迟、幅度和相位的求解表达式,分析了延迟样式以及幅度和相位控制误差对干扰抵消效果的影响。
本文其余部分是这样安排的:第2节是系统模型;第3节是幅度和相位误差对自干扰抵消性能的影响分析,并给出理论表达式;第4节给出了理论分析值和仿真值;最后是论文的总结。
2 系统模型
2.1 信号模型
同频全双工的系统架构如图1所示,近端发射机信号s( t)送入环形器后通过单天线辐射出去,d( t)为本地接收机接收到的远端发射机信号[14]。由于环形器的有限隔离,发射机信号通过环形器耦合进入接收机,同时通过空间反射进入接收机,形成自干扰信号 sI(t)。图1中给出了多抽头模拟抵消方案,耦合部分发射机信号,送入自干扰抵消单元。自干扰抵消单元的每个抽头具有不同的延迟、相位和幅度,每个抽头的延迟是根据硬件设计预先确定的固定值,而相位和幅度则是可控制的变量。近端接收机首先估计自干扰信道,然后根据特定算法,生成相应的幅度和相位控制字,合成相应的自干扰对消信号为(t),用于自干扰抵消[15]。

图1 同频全双工无线电系统结构
近端接收机的射频信号可以表示为

式中,d( t)表示接收到的用来解码的期望信号,sI(t)表示自干扰信号,ˆ sI(t)表示本地合成的自干扰对消信号,n( t)表示高斯白噪声,假设n( t)~N(1,σ2)。
近端接收机的自干扰射频信号 sI(t)可以表示为

式中,c表示耦合器的耦合系数,取值范围为(0,1),(1-c)表示定向耦合器主通道的通过信号幅度,s( t) 为发射机信号, hI(t)表示自干扰信号,由环形器泄露信道 hc(t)和空间反射信道 hr(t)相加而得,一般来说, hc(t)的能量要比 hr(t)大至少30 dB。*表示发射机和自干扰信道的卷积。
近端接收机中本地合成的自干扰对消射频信号的 ˆsI(t) 可以表示为

式中,N为模拟对消单元通道数, N ≥ 2 , ai( i=1,2,…,N),φi(i = 1 ,2,… ,N ) 和di( i = 1 ,2,…, N ) 分别为模拟对消单元每条支路对应的延迟线大小、移相器值和幅度衰减值。
在发射机训练周期信号发射期间,假设()d t=0,则近端接收机接收到的射频信号表示为

其中 eR(t)为残余自干扰射频信号,表示为

2.2 优化求解
在任意特定的时间段内,假设为 [t1, t2] ,(t1< t2),为了使近端接收机的残余干扰信号最小,对近端接收机接收到的信号r( t)进行幅度平方积分,并求取期望,则优化目标函数表示为


优化求解问题可以表示为其中a表示多抽头自干扰合成单元的幅度控制向量,一般比自干扰信号功率大几倍,因此一般不考虑幅度限制,φ表示多抽头自干扰合成单元的相位控制向量,ao和 φo表示求解出的最优幅度和相位控制向量值。
假设n( t)与ˆsI(t) 和sI(t)相互独立,则有n( t)与eR(t)相互独立,那么优化目标函数展开为
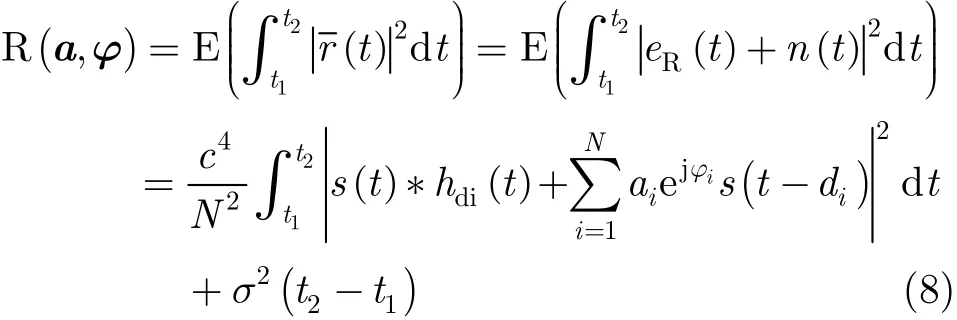
式中, hdi(t)表示等效自干扰信号,表示为

在能量检测时间 ( t2-t1)内应用帕斯瓦尔定理[16],假设信道带宽为B,中心频率为 fc,转换到频域求解:

其中,s(j2πf)为近端发射信号s( t)的傅里叶变换,hdi(j2 π f)为hdi(t) 的傅里叶变化。
通过柯西不等式可得

由式(11)可知,当s(j2πf)能量谱近似为常数,可使式(11)的等号成立。因此求 R ( a, φ )的最优 ao和φo,等效为求解式(12)的 ao和 φo:

上述问题是一个非凸优化问题[17],求解困难。实际系统中,当信道采样为有限点,设为M。假设信道为慢衰落信道,在一定时间,估计信道值为

式中, f1,f2,… ,fM为信道采样频率点。
幅度相移控制向量和延迟频率采样矩阵分别为

式(12)可以转化为

在实际设计中,一般MN≫,根据广义逆矩阵最小范数解[18],式(16)的最优解为

其中,D+(f)为最小范数广义逆,定义为D+(f)=DH(f ) (D ( f ) DH( f ) )-1, H为哈密特转置。
总结上述,干扰消除的调控算法为:
步骤 1 自干扰信号同步,例如:采用 ZC(Zadoff-Chu) 序列时,可采用互相关算法进行同步;
步骤 2 通过信道估计,如线性最小均方误差(Linear Minimum Mean Square Error, LMMSE),估计信道为 hk(f),其中k表示信道估计时刻;
步骤 3 如果 hk(f ) = hk-1(f ) ,等待下一个自干扰消除周期,转到步骤2,否则转到步骤4;
步骤 4 通过式(17),求解出每个抽头对应的移相器值 ao和幅度衰减值 φo;
步骤 5 DAC输出 ao和 φo的模拟值,完成一次射频干扰抵消,等待下一个干扰消除周期,转到步骤2。
3 性能分析
假设信道参数理想估计,根据式(17)计算出通道幅度和相位

以使残余自干扰最小。下文分析,当存在幅度和相位控制量化误差时,对干扰对消效果的影响。
3.1 幅度量化控制误差
假设每个通道,幅度量化间隔相等为σA,设其量化误差ξA为(- σA/2,σA/2) 的均匀分布,则有

所有通道的量化误差 ξAi(i = 1,2,… ,N)跟 ξA同分布,且相互独立,则有

自干扰抵消残余信号功率设为RP,可以表示为

当对信道进行M个点离散采样时,关系式为

由式(22),式(20)和式(21),得到幅度量化最小间隔Aσ与射频自干扰抑制能力关系为

从式(23)可以看出,为了达到更好的干扰抵消效果,幅度控制量化最小间隔Aσ越小越好。
3.2 相位量化控制误差
假设每个通道,幅度间隔为φA,设其量化误差ξφ为 ( - φA/ 2,φA/2)的均匀分布,则有
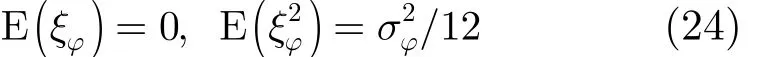
所有通道的量化误差 ξφi(i = 1,2,… ,N) 跟 ξφ同分布,且相互独立,式(22)可以变为

式中,(a)的成立条件是 ξφi( i = 1 ,2,…, N ) 很小。
当相位误差较小时,由式(21),式(22)和式(25),得到相位间隔σφ与射频自干扰抑制能力关系式为

从式(26)可以看出,为了使干扰抵消效果更好,相位控制量化最小间隔φσ越小越好。
4 数字及仿真结果
仿真信道为莱斯信道,带宽为100 MHz,信道采样点M设置为10,多径数为3,分别为1条由泄露和失配引起的自干扰信道主径和 2条空间反射径。设自干扰信道中主径的功率为R dBm,延迟为8 ns,另外两条多径的延迟和相对幅度分别为:20 ns,-40 dB, 60 ns和 40 dB- 。在分析仿真幅度和相位控制误差对自干扰抵消性能的影响前,需要确定各个抽头的延迟参数,因此对不同的延迟样式对干扰抵消进行仿真分析。
首先,固定抽头数为 4,通过改变抽头的最大延迟,设为dns,则各个抽头延迟等间隔设置为0 ns,d/3 ns, 2d/3 ns, d ns,观察抽头最大延迟的改变对干扰抵消效果的影响。当自干扰信号主径功率R为0 dBm时,仿真结果如图2和图3所示。从图2中可以看出,当d小于8 ns的时候,干扰抵消值随着d的增大而增大,而当自干扰信道主径的延迟在抽头延迟范围内,干扰抵消效果最好。而当d大于14 ns的时候,干扰抵消值的整体趋势是随着d的增大而变小,除24 ns附近的尖峰,此尖峰是在有固定抽头延迟为8 ns的时候发生。上述结果表明,抽头延迟覆盖了自干扰信道主径延迟的基础上,且要求各个抽头的延迟设置不要太分散,如果过于分散,干扰抵消效果将下降。图3仿真了自干扰带宽分别为100 MHz, 50 MHz和25 MHz情况下,不同的d对自干扰抵消的影响。无论d的取值如何,干扰抵消值都随着自干扰带宽减小而显著增加,特别是当d的取值比较大,即各个抽头的间隔比较大的时候,自干扰信号带宽越小,干扰抵消效果越好。

图2 不同的抽头延迟参数对射频干扰抵消的影响

图3 不同自干扰带宽下不同的抽头 延迟参数对射频干扰抵消的影响

4 不同的抽头个数对射频 干扰抵消的影响
其次,固定最大的抽头延迟d为68 ns,最小抽头延迟为0 ns,保证延迟范围覆盖所有的自干扰信道的多径。然后通过改变抽头的个数,观察抽头个数增加对自干扰抵消效果的影响,如图4所示。当抽头数为 2~16个时,设置抽头延迟分布为等间隔均匀分布,采样点数M设置为抽头个数的2.5倍。仿真结果如图4所示,可以看出,射频自干扰抵消能力随着抽头个数的上升而上升,在抽头数低于 6个时,干扰抵消效果上升并不明显,说明抽头个数过少,对多径自干扰的去除能力有限,当抽头个数大于6个时,干扰抵消效果跟着抽头个数有显著上升。当自干扰信号主径功率R为32 dBm时,在抽头个数为16个时,干扰抵消可达125.5 dB;当自干扰信号主径功率R为0 dBm时,在抽头个数为15个时,干扰抵消已达白噪声底线的最大值94.0 dB。
最后,仿真抽头幅度和相位控制误差对射频干扰抵消的影响。自干扰信号主径功率R为0 dBm,多抽头干扰抵消器采用4抽头,延迟设置如表1所示,通过式(17),计算出每个抽头的幅度和相位值,各个抽头的幅度值是跟自干扰主径信号功率的相对值,如表1所示。
从图5可以看出,幅度相对控制误差对射频干扰抵消影响的分析值和仿真值完全吻合,图中幅度相对控制差值是幅度控制误差相对于最大幅度多径的比值,当幅度相对控制误差为0.005,幅度相对控制误差对干扰抵消基本无影响,接近36.89 dB的干扰抵消最优值;随着幅度相对控制误差的增加,幅度相对控制误差对干扰抵消的影响越来越大;当幅度相对控制误差为0.08时,干扰抵消值下降到28.94 dB,相对于最优值已经下降了7.95 dB。

表1 多抽头固定延迟参数设置

图5 幅度控制误差对射频干扰抵消的影响
从图6可以看出,相位相对控制误差对射频干扰抵消影响的分析值和仿真值完全吻合,图中相位控制差值是实际相位误差跟360°的比值,当相位相对控制误差为0.005,相位相对控制误差对干扰抵消基本无影响,接近36.66 dB的干扰抵消最优值;随着相位相对控制误差的增加,相位相对控制误差对干扰抵消的影响越来越大;当相位相对控制误差为0.08时,干扰抵消值下降到23.91 dB,相对于最优值已经下降了12.75 dB。
5 结束语
本文针对全双工同时同频系统中多抽头射频干扰抵消抑制方法,首先根据得出的最优化公式,仿真分析不同的抽头个数和抽头延迟间隔对射频自干扰抵消的影响;其次分析了由于器件的控制精度引起的幅度和相位控制误差对射频自干扰抵消的影响,推导了幅度和相位控制误差对自干扰抵消的理论表达式,并用仿真验证了理论的正确性。本文的研究结果可作为幅度和相位控制精度选择的重要依据。

图6 相位控制误差对多抽头射频干扰抵消效果的影响
[1] Elsayed A, Eltawil A M, and Sabharwal A. Rate gain region and design tradeoffs for full-duplex wireless communications[J]. IEEE Transactions on Wireless Communications, 2013,12(7): 3556-3565.
[2] 张志亮, 罗龙, 邵士海, 等. ADC 量化对同频全双工数字自干扰消除的误码率性能分析[J]. 电子与信息学报, 2013, 35(6):1331-1337.Zhang Zhi-liang, Luo Long, Shao Shi-hai, et al.. Analysis of ADC guantizing affection on SER performance of self-interference canceling common-frequency full-duplex system[J]. Journal of Electronics & Information Technology,2013, 35(6): 1331-1337.
[3] 王俊, 赵宏志, 卿朝进, 等. 同时同频全双工场景中的射频域自适应干扰抵消[J]. 电子与信息学报, 2014, 36(6):1435-1440.Wang Jun, Zhao Hong-zhi, Qing Chao-jin, et al.. Adaptive self-interference cancellation at RF domain in co-frequency co-time full duplex systems[J]. Journal of Electronics &Information Technology, 2014, 36(6): 1435-1440.
[4] Syrjala, V, Valkama, M, Anttila, L, et al.. Analysis of oscillator phase-noise effects on self-interference cancellation in full-duplex OFDM radio transceivers[J]. IEEE Transactions on Wireless Communications, 2014, 13(6):2977-2990.
[5] Sahai A, Patel G, and Sabharwal A. Pushing the limits of full-duplex: design and real-time implementation[R]. The Computing Research Repository (CoRR), 2011.
[6] Chan P W C, Lo E S, and Wang R R. The evolution path of 4G networks: FDD or TDD?[J] IEEE Communications Magazine, 2006, 44(12): 42-50.
[7] Lee W C Y. The most spectrum-efficient duplexing system:CDD[J]. IEEE Communications Magazine, 2002, 40(3):163-166.
[8] Choi J I, Jain M, Srinivasan K, et al.. Achieving single channel, full duplex wireless communication[C]. Proceedings of the 16th Annual International Conference on Mobile Computing and Networking (MobiCom '10), New York, USA,2010: 1-12.
[9] Khojastepour M A, Sundaresan K, Rangarajan S, et al.. The case for antenna cancellation for scalable full-duplex wireless communications[C]. Proceeding of the 10th ACM Workshop on Hot Topics in Networks (HOTNETS), Massachusetts,USA, 2011: 17.
[10] Jain M, Choi J I, Kim T M, et al.. Practical, real-time, full duplex wireless[C]. Proceedings of the 17th Annual International Conference on Mobile Computing and Networking (MobiCom,11), New York, USA, 2011: 301-312.
[11] 徐强, 全欣, 潘文生, 等. 同时同频全双工LTE射频自干扰抑制能力分析及实验验证[J]. 电子与信息学报, 2014, 36(3):662-668.Xu Qiang, Quan Xin, Pan Wen-sheng, et al.. Analysis and experimental verification of RF self-interference cancelation for co-time co-frequency full-duplex LTE[J]. Journal of Electronics & Information Technology, 2014, 36(3): 662-668.
[12] Hong S, Mehlman J, and Katti S. Picasso: flexible RF and spectrum slicing[C]. Proceedings of the ACM SIGCOMM 2012 Conference on Applications, Technologies,Architectures, and Protocols for Computer Communication(SIGCOMM), Helsinki, Finland, 2012: 37-48.
[13] Radunovic B, Gunawardena D, Key P, et al.. Rethinking indoor wireless mesh design: low power, low frequency,full-duplex[C]. Proceedings of the Fifth IEEE Workshop on Wireless Mesh Networks (WIMESH), Boston, USA, 2010:1-6.
[14] Knox M E. Single antenna full duplex communications using a common carrier[C]. Proceedings of the IEEE 13th Annual Wireless and Microwave Technology Conference(WAMICON), Florida, USA, 2012: 1-6.
[15] Bharadia D, McMilin E, and Katti S. Full duplex radios[C].Proceedings of the ACM SIGCOMM 2013 Conference on SIGCOMM (SIGCOMM,13), New York, USA, 2013: 375-386.
[16] Oppenheim A V, Willsky A S, and Nawab S H. Signals and Systems[M]. 2nd Edition, Upper Saddle River: Prentic Hall,1996: 312.
[17] McMichael J G and Kolodziej K E. Optimal tuning of analog self-interference cancellers for Full-Duplex wireless communication[C]. Proceedings of the 50th Annual Allerton Conference on Communication, Control, and Computing(Allerton), Monticello, USA, 2012: 246-251.
[18] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004:81-87.

