一种基于瞬时相位方差加权的线谱检测器

郑恩明 余华兵 陈新华 孙长瑜

1 引言

由于被动声呐不主动对外辐射信号，隐蔽性较强，一直是对水下目标进行检测、定位、跟踪、识别重要手段之一。但随着隐身技术的不断提高，被动声呐接收数据的信噪比随之在不断降低，对被动声呐的性能需求也越来越严格。被动声呐常用的检测技术 能量累积检测方法，现已不能满足远程目标检测需求。学者通过理论和实验证明了：水下目标辐射噪声中含有丰富的单频分量，特别是在低频段，螺旋桨转动会切割水体产生低频信号，一部分低频分量直接以加性形式出现在目标辐射信号中，另有部分被船体自身振动调制到较高频带[16]-，线谱谱级通常比连续谱平均谱级高出 10～25 dB。这为被动声呐实现水下目标远程探测提供一种可能，也促使了线谱检测技术的进一步发展。

依据水下目标辐射噪声含有高强度稳定线谱这一特征，国内外学者在不同方面进行了有效、有针对性研究，提高了被动声呐性能[715]-。文献[9,10]提出了一种基于瞬时频率方差加权的阵列信号处理方法，文献[11]提出了一种基于瞬时方位方差加权的阵列信号处理方法，它们均克服了传统线谱检测4维显示难点，改善了能量累积检测法在远程目标检测方面的性能。文献[12]提出了一种基于瞬时频率方差加权的时延估计方法，文献[13,14]提出了一种基于瞬时时延差方差加权的时延估计方法，它们均提高了互相关法在远程目标定位方面的性能。

另外，在线谱检测检测方面，国内外学者做了不少研究，并取得了一定的研究成果，尤其是在相位差分补偿、对齐方面[1620]-。文献[16]利用线谱信号与背景噪声间的时间相关半径与相位起伏均匀性差异，提出了一种基于信号起伏相位差分对齐的相干检测方法，抑制了背景噪声能量干扰。文献[17,18]利用相位起伏特性，改善了对目标的监测性能和线谱信号与背景噪声的时间相关半径。文献[19]提出了一种差分二次平均修正的频域相位补偿线谱检测方法，该方法与文献[16]相似。同样，文献[20]给出了正弦信号的直接 FFT 参数估计与相位差分法对比研究结果。但这些方法均是基于相位差分一阶矩信息进行相位对齐或补偿来提高FFT参数估计效果，均没有利用相位差分前后的相位方差二阶矩信息。

[9-14]所提出的加权思想启发，本文依据水下目标辐射噪声含有高强度稳定线谱这一特征，利用目标线谱频率单元对应瞬时相位比较稳定，背景噪声频率单元对应瞬时相位比较随机的特点，提出一种基于瞬时相位方差加权的线谱检测方法。该方法相比相位差分对齐或补偿法[1620]-可以进一步增强目标线谱检测信噪比增益，抑制背景噪声能量干扰，实现对水下目标辐射噪声中未知线谱的检测。并通过理论分析和实验结果验证了本文方法可以进一步增强目标线谱能量、抑制噪声、提高信噪比，在抗复杂信道检测、识别领域具有良好的应用前景。

2 信号模型

水下目标辐射信号简化形式可表示为[5]

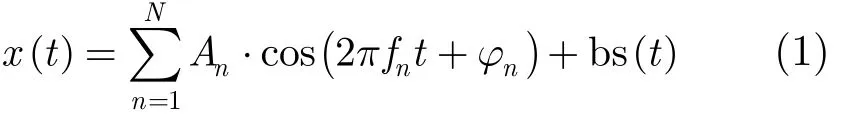
式中，nA为线谱信号幅度，nf为线谱信号频率，nφ为线谱信号初始相位，t为目标辐射信号时刻，（）bs t为宽带信号；N为假定的独立分量数，nφ和（）bs t相互独立，nφ服从[02]π～均匀分布。

以式（1）中第n个线谱信号分量为例，其与宽带信号平均谱级比为

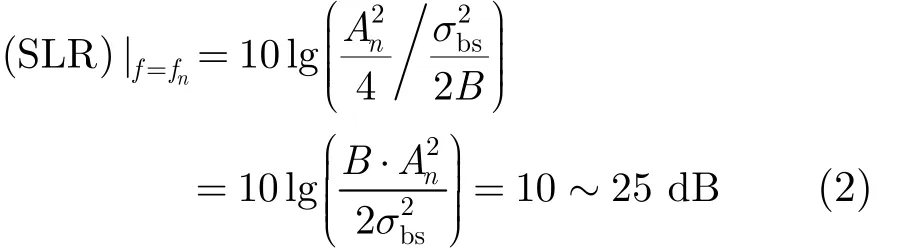
由式（2）可知，目标辐射信号的线谱信号谱级远高于宽带信号平均谱级。若要检测目标，可通过检测线谱信号来实现。

3 基于瞬时相位方差加权的线谱检测法

由于FFT分析法处理增益较大，在检测具有强线谱目标时，常被采用。由于背景噪声频谱值起伏很大，常规FFT分析法所得最终频谱会存在线谱信号被淹没在背景噪声中情况，不便于线谱检测。对此，本文对常规FFT分析法做了进一步改进处理，以增强目标线谱能量、抑制噪声、提高信噪比。

3.1 算法基本原理

假设目标辐射信号具有稳定线谱，统计时间内线谱相位或差分相位变化缓慢，可以采用下述方法实现线谱检测。

首先对采集数据分块做FFT分析，所得频谱记为X（ m, fk）,m =1,2,… ,M ,k = 1 ,2,…, K ； 其中，M为采集数据分块数，K为每块FFT分析所得频率单元数。

然后对每块 FFT分析结果所有频率单元进行瞬时相位提取，记为φ（m, fk）,m=1,2,…,M, k=1,2,…,K。

如果采用常规FFT分析法进行线谱检测，最终频谱可按式（3）表示：

在滤波器频带 B = f1～ fK内，当目标辐射信号只占据某一个或某几个频率单元时，如果采用式（3）求取最终频谱，则会将所有频率单元对应谱值等价地加权到最终频谱中。由于背景噪声频谱值起伏很大，最终频谱受噪声影响较大，不便于最后线谱检测。对此，利用线谱频率单元与噪声频率单元对应瞬时相位在二阶矩上的差别，对各频率单元进行加权求和，削弱噪声对最终频谱影响，增强线谱检测信噪比增益，抑制背景噪声能量干扰，可将式（3）变换为

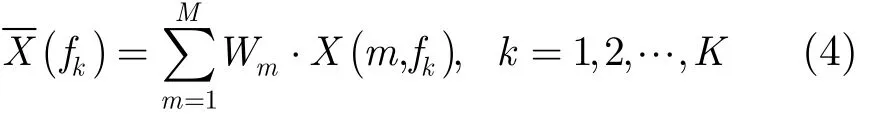
式中，mW 为不同频率单元所需权值。

基于瞬时相位方差加权的线谱检测流程图如图1 所示。

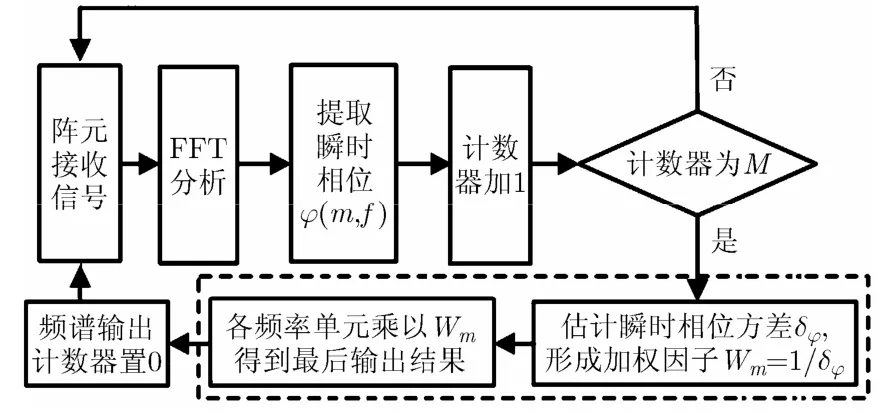
图1 基于瞬时相位方差加权的线谱检测流程图

图中虚线部分既为本文对 FFT分析法所做改进。

3.2 算法实现

依据图1所示流程图，本文方法实现过程可分为以下5个步骤：

步骤 1 对阵元拾取数据进行滤波放大，然后通过A/D电路采样，采样率为 fs，得到离散信号x（ n' Ts） ，其中，Ts=1/fs,n ' = 1 ,2,… ,N ',N'为数据长度；

步骤2 按式（5）对x（ n'Ts）做FFT分析，并提取X（ kws）中各频率单元瞬时相位；为了充分利用所得信号，本文采用α-β滤波器得到本次所需频谱。

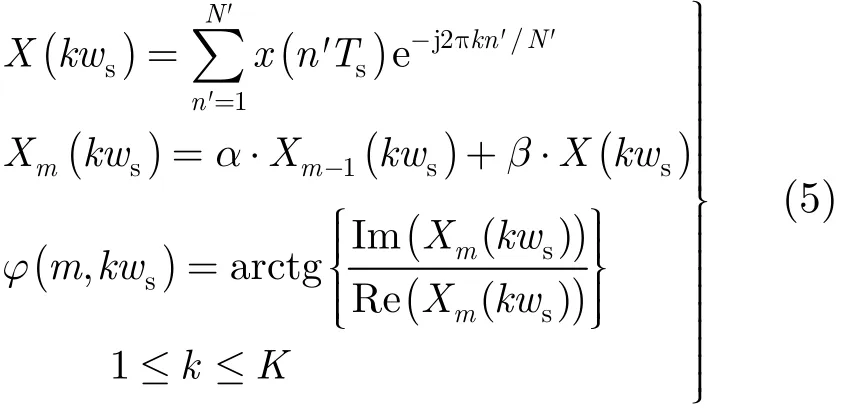
式中，ws= 2π/ KTs是FFT分析中的频率采样间隔。Xm（kws） 叠加了频谱数据Xm-1（kws） ，其中，1≤m≤M ,M为统计次数，X0（kws）=0,α =β=0.5为本文所用滤波器系数；

步骤3 更新接收信号，重复进行步骤1、步骤2，直到重复次数达到预先设定值M，则各频率单元均得到M个瞬时相位值，记为 φ （ m, kws）, m =1,2,…,M,k = 1 ,2,…, K ；

步骤 4 对所有频率单元的瞬时相位值按式（6）进行方差计算，记为 δφ（ k ws）,k = 1 ,2,… , K 。

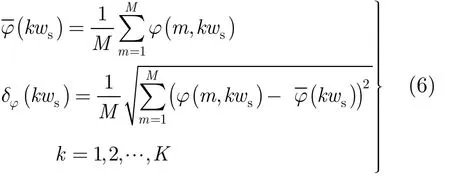
步骤 5 对所有频率单元进行瞬时相位方差加权统计，得到最终频谱和信号线谱估计值。如式（7）所示。

当 δφ（ k ws） 较小时，其对应频率单元谱值在X（ kws）中数值较大，便于检测提取。

3.3 算法性能分析

设滤波器频带上下限为 f1,fK，目标线谱占其中一个频率单元。最小和最大预成瞬时相位值为φ1,φL，目标线谱频率单元瞬时相位值的最小值和最大值分别为φmin, φmax。进行M帧统计，假设所有频率单元瞬时相位值均服从均匀分布，背景噪声和目标线谱瞬时相位方差分别为δn, δs。

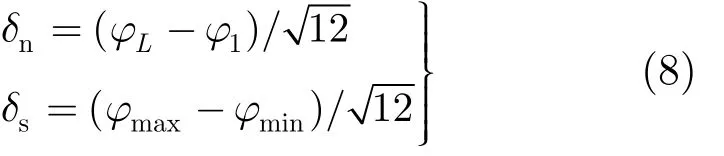
首先对背景噪声频率单元进行统计，对于背景噪声频率单元，每个预成瞬时相位值出现概率相等。

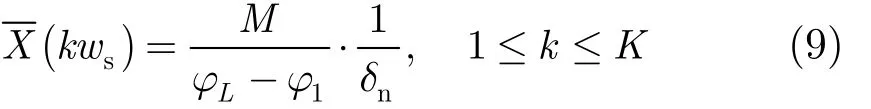
然后将目标线谱瞬时相位方差结果累加到式（9）中，可得

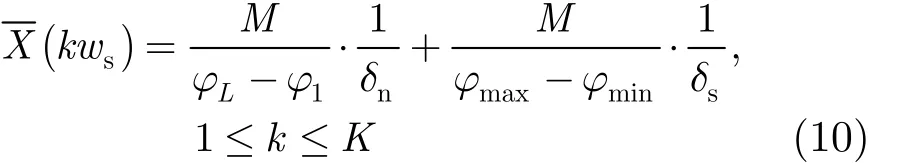
式（10）可简化为

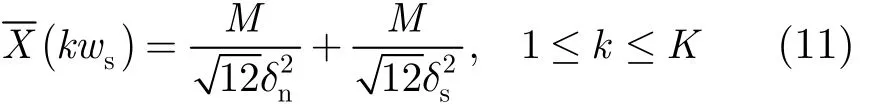
所以当目标线谱相位比较稳定被正确估计的概率在50%以上时，通过排序、提取中间部分值可使相位方差值 δs＜＜δn；当目标线谱频率单元对应瞬时相位受水声信道影响产生波动时，可对各频带瞬时相位先进行差分对齐，然后再求取相位差分对齐后的相位方差值。此时由文献[16]可知目标线谱频率单元对应瞬时相位差分值比较稳定，背景噪声频率单元对应瞬时相位差分值比较随机，进而可得相位差分对齐后的相位方差值 δs＜＜ δn，由式（11）可知：在频谱输出值中，目标线谱频率单元对应谱值将远大于其它位置对应谱值。

依据水下目标辐射噪声的线谱幅值明显高出连续谱幅值。现假定目标辐射信号只有线谱分量，线谱 1，线谱 2频率分别为69 Hz和100 Hz，干扰为带限噪声，带宽为10 ～ 5 00 Hz。图2，图3和图4分别是3种方法从输入平均谱级比-30～30 dB，每个平均谱级比下做 1000次独立统计所得线谱频率单元与噪声频率单元的瞬时相位标准差和最终线谱频率单元与噪声频率单元的平均谱级比，每次采集长度为 T = 1 0 s，对采集数据分10段进行FFT分析。

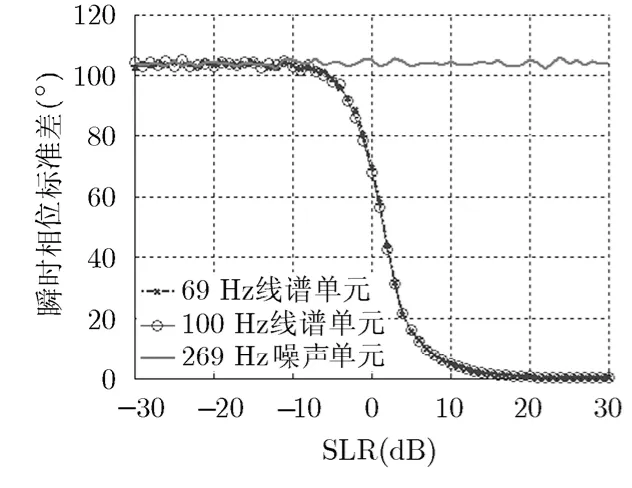
图2 不同输入平均谱级比下的瞬时相位标准差

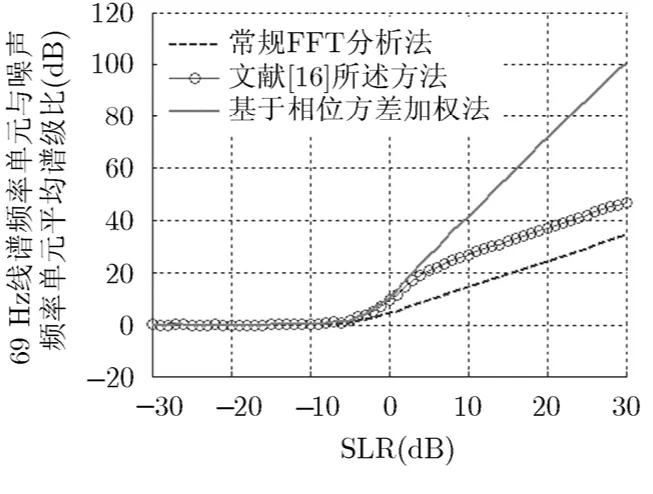
图3 不同输入平均谱级比下，3 种方法所得69 Hz线谱频率单元与噪声频率单元平均谱级比

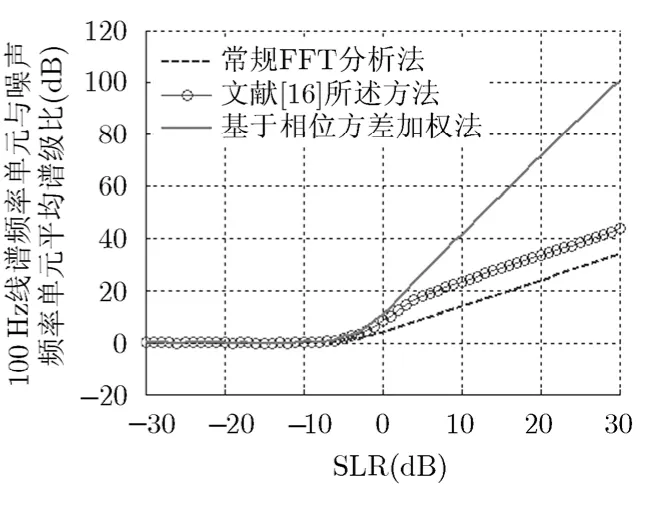
图4 不同输入平均谱级比下，3 种方法所得100 Hz线谱频率单 元与噪声频率单元平均谱级比

由图2可知，在输入平均谱级比高于-6 dB时，目标线谱频率单元瞬时相位标准差小于噪声频率单元的瞬时相位标准差。由图 3 和图4可知，相比常规FFT分析法、文献[16]所述方法所得最终线谱频率单元与噪声频率单元的平均谱级比，在输入平均谱级比大于 6 dB- 时，本文方法所得最终线谱频率单元与噪声频率单元的平均谱级比得到了提高，且随着输入平均谱级比越高，输出线谱频率单元与噪声频率单元的平均谱级比被提高越多。原因在于在相位存在波动时，每一时刻所得频谱相位并非完全一致，常规FFT分析法在没有进行相位对齐时，求得的最后频谱并非为线谱真实幅值的绝对累加，而文献[16]所述方法是先对每一时刻所得频谱相位进行对齐，然后采用式（3）求取最后频谱，所得最后频谱为线谱真实幅值的绝对累加。所以输入平均谱级比大于-6 dB时，文献[16]所述方法相比常规 FFT分析法所得最后频谱的线谱频率单元与噪声频率单元的平均谱级比得到了提高；且在高信噪比下，线谱真实幅值的绝对累加与非真实幅值的绝对累加差别基本不变，所以在输入平均谱级比大于5 dB，文献[16]所述方法相比常规FFT分析法所得最后频谱的线谱频率单元与噪声频率单元的平均谱级比的差值基本不变。在相位存在波动时，本文方法先对每一时刻所得频谱相位进行差分对齐，然后再求取相位方差，最后采用式（7）求取最后频谱，由于δs＜＜δn，所得频谱的线谱频率单元与噪声频率单元的平均谱级比得到了进一步提高。在仿真情况下，输入谱级比越高，δs越小，所得频谱的线谱频率单元与噪声频率单元的平均谱级比提高越大。

4 实验结果

本次海试数据为2014年7月在南海进行相关海试采集存储所得。当时海深80 m左右，海底平坦，海况3级左右。试验所用目标船和接收设备如图5所示，潜标所连水听器布放于60 m深度，目标船在潜标1 km附近运动，水听器所接采集设备采样率为20 kHz。

图6～图10为一次采集长度为 5 s T= ，对采集数据分5段进行 FFT分析，然后再分别按式（3）、文献[16]所述方法和式（7）所得最终频谱图、输出线谱频率单元与噪声频率单元平均谱级、瞬时相位标准差和LOFAR图。

由图6结果可知，相比常规FFT分析法、文献[16]所述方法，本文方法可有效增强目标线谱能量、抑制噪声、提高信噪比；在t=300 s数据段中，本文方法相比文献[16]所述方法所得 69 Hz处线谱频率单元平均谱级提高了近7 dB, 107 Hz处线谱频率单元平均谱级提高了近 14 dB；本文方法相比常规FFT分析法所得69 Hz处线谱频率单元平均谱级提高了近5 dB, 107 Hz处线谱频率单元平均谱级提高了近12 dB。原因可由图7得，在大部分时间段内，δs＜＜ δn，经式（7）处理后，所得频谱的线谱频率单元谱级相比噪声频率单元谱级被有效扩大，所以可得在其他时间数据段中，本文方法相比常规FFT分析法、文献[16]所述方法在69 Hz, 107 Hz处线谱频率单元平均谱级提高更多。

同样，对比图 8至图10可知，常规FFT分析法已不能检测到 69 Hz处目标线谱信号，文献[16]所述方法虽然能检测到69 Hz处目标线谱信号，但与背景噪声谱级差别不大，而本文方法可以有效检测到69 Hz处线谱频率单元信号，且与背景噪声谱级差别较大；且对于107 Hz处线谱频率单元信号的检测效果，本文方法远好于FFT法分析法、文献[16]所述方法。

5 结束语

本文依据水下目标辐射噪声含有高强度稳定线谱这一特征，介绍了一种基于瞬时相位方差加权的线谱检测方法。本文方法首先对接收信号做FFT，然后对所有频率单元均进行瞬时相位提取，利用目标线谱频率单元对应瞬时相位比较稳定，背景噪声频率单元对应瞬时相位比较随机的特点，对各频率单元进行瞬时相位方差加权统计，进一步抑制了背景噪声能量干扰，增强了目标线谱检测信噪比增益。在本文仿真条件下，相比常规FFT分析法、相位差分对齐法[16]所得最终线谱频率单元与噪声频率单元的平均谱级比，在输入平均谱级比大于-6 dB时，本文方法所得最终线谱频率单元与噪声频率单元的平均谱级比得到了进一步提高，且随着输入平均谱级比越高，输出线谱频率单元与噪声频率单元的平均谱级比提高越多。海试数据处理结果同样验证了本文所提方法相比常规FFT分析法、相位差分对齐法，进一步抑制了背景噪声能量干扰，增强了目标线谱检测信噪比增益，实现了对水下目标辐射噪声中未知线谱的检测。另外，在目标线谱频率单元对应瞬时相位受水声信道影响产生波动时，可对各频带瞬时相位先进行差分对齐，然后再求取相位差分对齐后的相位方差值。

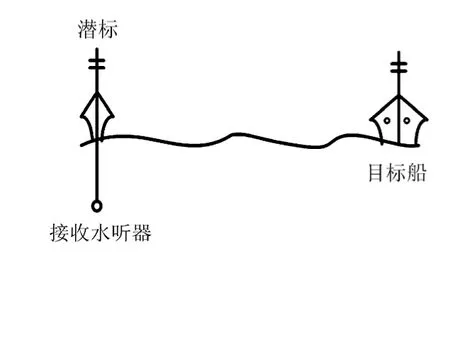
图5 海试试验系统图

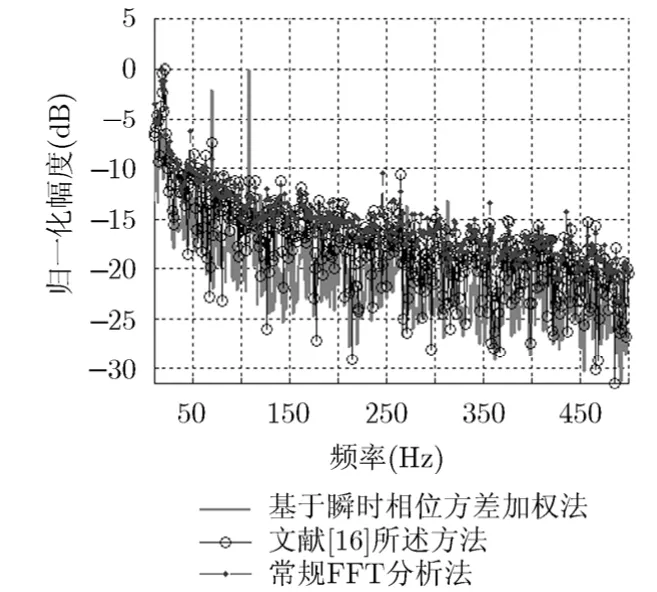
图6 3种方法所得最终频谱图（t=300 s）

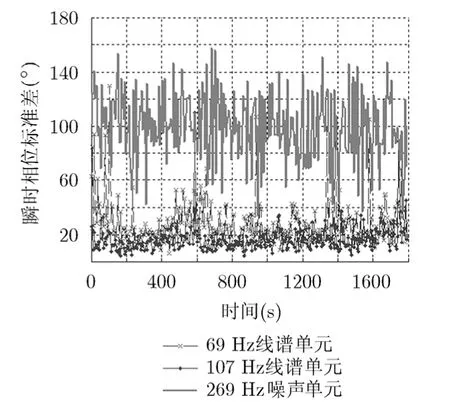
图7 瞬时相位标准差

图8 常规FFT分析法所得最终LOFAR图

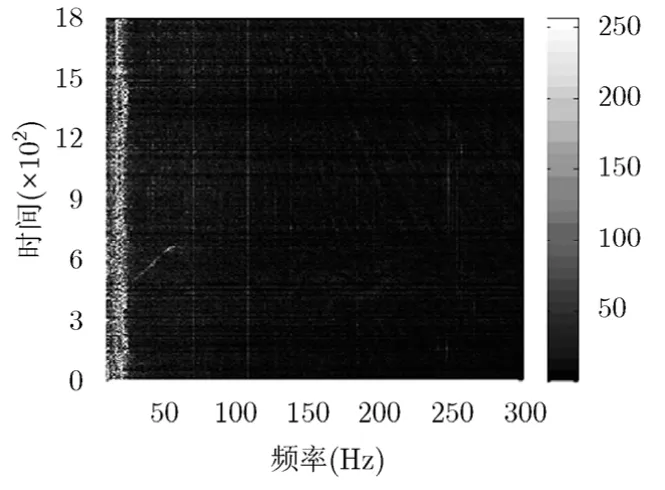
图9 文献[16]所示方法所得 最终LOFAR图

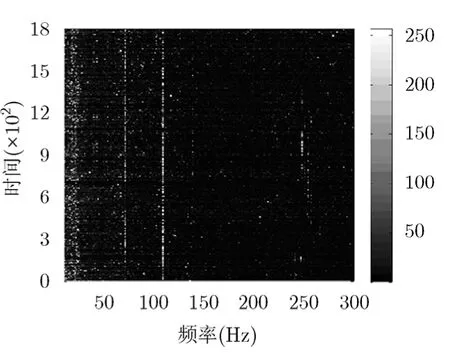
图10 基于瞬时相位方差加 权法所得最终LOFAR图

参 考 文 献

[1] Urick R J. Principles of Underwater Sound[M]. New York:McGraw-Hill Book Company, 1983: 61-79.

[2] Ross D. Mechanics of Underwater Noise[M]. New York:Pergmin Press, 1976: 83-89.

[3] Crocker S E, Nielesen P L, Miller J H, et al.. Geoacoustic inversion of ship radiated noise in shallow water using data from a single hydrophone[J]. Journal of the Acoustical Society of America, 2014, 136（5）: 362-368.

[4] Megan F, Donald R, and Sean M. Underwater radiated noise from modern commercial ships[J]. Journal of the Acoustical Society of America, 2012, 131（1）: 92-103.

[5] 李启虎, 李敏, 杨秀庭. 被动目标辐射噪声中单频信号分量的检测: 理论分析[J]. 声学学报, 2008, 33（3）: 193-196.Li Qi-hu, Li Min, and Yang Xiu-ting. The detection of single frequency component of underwater radiated noise of target:theoretical analysis[J]. Acta Acustica, 2008, 33（3）: 193-196.

[6] 李启虎, 李敏, 杨秀庭. 被动目标辐射噪声中单频信号分量的检测: 数值仿真[J]. 声学学报, 2008, 33（4）: 289-293.Li Qi-hu, Li Min, and Yang Xiu-ting. The detection of single frequency component of underwater radiated noise of target:digital simulation[J]. Acta Acustica, 2008, 33（4）: 289-293.

[7] Tucker J D and Azimi-Sadjadi M R. Coherence-based underwater target detection from multiple disparate sonar platforms[J]. IEEE Journal of Oceanic Engineering, 2011,36（1）: 37-51.

[8] 吴国清, 王美刚, 陈耀明. 水声波导中包络线谱强度数值预报[J]. 声学学报, 2013, 37（4）: 432-439.Wu Guo-qing, Wang Mei-gang, and Chen Yao-ming.Numerical prediction of envelope line spectrum intensity in underwater acoustic waveguide[J]. Acta Acustica, 2013, 37（4）:432-439.

[9] 陈阳, 王自娟, 朱代柱, 等. 一种基于频率方差加权的线谱目标检测方法[J]. 声学学报, 2010, 35（1）: 76-80.Chen Yang, Wang Zi-juan, Zhu Dai-zhu, et al.. A detecting method for line-spectrum target based on variance of frequency weight[J]. Acta Acustica, 2010, 35（1）: 76-80.

[10] 陈阳, 赵安邦, 王自娟, 等. 瞬时频率方差加权导向最小方差波束形成检测器[J]. 哈尔滨工程大学学报, 2011, 32（6）:730-735.Chen Yang, Zhao An-bang, Wang Zi-juan, et al.. Variance of instantaneous frequency-weighted steered minimum variance beamforming detector[J]. Journal of Harbin Engineering University, 2011, 32（6）: 730-735.

[11] 陈新华, 鲍习中, 李启虎, 等. 水下声信号未知频率的目标检测方法研究[J]. 兵工学报, 2012, 33（4）: 471-475.Chen Xin-hua, Bao Xi-zhong, Li Qi-hu, et al.. Research on detection of underwater acoustic signal with unknown frequency[J]. Acta Armamentarii, 2012, 33（4）: 471-475.

[12] 郑恩明, 陈新华, 孙长瑜. 基于频率方差加权的时延差估计方法[J]. 系统工程与电子技术, 2014, 36（2）: 224-229.Zheng En-ming, Chen Xin-hua, and Sun Chang-yu. The time delay difference estimation weighted method based on frequency variance[J]. Systems Engineering and Electronics,2014, 36（2）: 224-229.

[13] 郑恩明, 陈新华, 孙长瑜, 等.基于时延差方差加权的时延差估计方法[J]. 电子与信息学报, 2014, 36（6）: 1362-1367.Zheng En-ming, Chen Xin-hua, Sun Chang-yu, et al..Weighted time delay difference estimation method based on Its variance[J]. Journal of Electronics & Information Technology, 2014, 36（6）: 1362-1367.

[14] 郑恩明, 陈新华, 孙长瑜. 一种水下声信号未知频率的时延差估计方法[J]. 振动与冲击, 2014, 33（9）: 190-194.Zheng En-ming, Chen Xin-hua, and Sun Chang-yu. A time delay difference estimation method of underwater acoustic sgnal with unknown frequency[J]. Journal of Vibration and Shock, 2014, 33（9）: 190-194.

[15] 张建, 关键, 董云龙, 等. 基于局部 Hilbert 谱平均带宽的微弱目标检测算法[J]. 电子与信息学报, 2012, 34（1）: 121-127.Zhang Jian, Guan Jian, Dong Yun-long, et al.. Weak target detection based on the average bandwidth of the partial hilbert spectrum[J]. Journal of Electronics & Information Technology, 2012, 34（1）: 121-127.

[16] 解恺, 丁雪洁, 孙贵青, 等. 基于目标辐射噪声的信号起伏检测算法研究[J]. 电子与信息学报, 2013, 35（4）: 844-851.Xie Kai, Ding Xue-jie, Sun Gui-qing, et al.. The signal fluctuating detection algorithm based on the target radiated noise[J]. Journal of Electronics & Information Technology,2013, 35（4）: 844-851.

[17] Venugopal S, Wagstaff R A, and Sharma J P. Exploiting phase fluctuations to improve machine performance monitoring[J]. IEEE Transactions on Automation Science and Engineering, 2007, 4（2）: 153-166.

[18] Wagstaff R A. Exploiting phase fluctuations to improve temporal coherence[J]. IEEE Journal of Oceanic Engineering,2004, 29（2）: 498-510.

[19] 戴文舒, 陈亚, 陈新华, 等. 差分二次平均修正的频域相位补偿线谱检测方法[J]. 兵工学报, 2014, 35（10）: 1630-1637.Dai Wen-shu, Chen Ya, Chen Xin-hua, et al.. An algorithm of line-spectrum detection uUsing frequency domain phase compensation with difference and TPM technique[J]. Acta Armamentarii, 2014, 35（10）: 1630-1637.

[20] 李辉, 王岩飞. 正弦信号的直接 FFT 参数估计与相位差分法对比研究[J]. 电子与信息学报, 2010, 32（3）: 544-547.Li Hui and Wang Yan-fei. The contrastive study between direct FFT and phase difference in parameter estimation of sinusoidal signal[J]. Journal of Electronics & Information Technology, 2010, 32（3）: 544-547.