亚麻纤维增强环氧树脂基复合材料拉伸强度的预测模型

吴 昊，花 军，刘 诚，范 豪，徐振锋

（东北林业大学机电工程学院，哈尔滨150040）

0 引 言

随着资源短缺及环境保护等问题的日益突出，开发以低价天然植物纤维替代合成纤维作为增强体的树脂基复合材料受到了世界各国的普遍重视。目前，探讨天然纤维增强树脂基复合材料制备工艺的文献和成果较多，但采用相关模型来预测其力学性能的研究不仅很少，而且预测精度均较低。Rouisona等［1］以洋麻纤维和不饱和聚酯树脂为主要原料，采用树脂传递模塑成型工艺制备了复合材料，并分析了复合材料的力学性能；Aziz等［2］着眼于改善复合材料的界面性能，对纤维进行碱处理，并探讨了碱处理对复合材料性能的影响；Feng等［3］研究了洋麻纤维和聚丙烯注射成型材料的热性能及动态热力学性能；张斌等［4］采用有限元法对织物增强复合材料的弹性模量进行了预测；才红［5］研究了剑麻纤维／酚醛树脂复合材料的性能；杨敏鸽等［6］研究了苎麻增强环氧树脂复合材料的力学性能；李小慧等［7］研究了聚酯纤维布增强环氧树脂基复合材料的拉伸性能和摩擦学性能。据所查资料显示，利用亚麻纤维和环氧树脂制备复合材料的研究还很少。

真空辅助树脂传递模塑工艺是一种新型的、制备低成本复合材料的成型技术，是一种在真空状态下排除纤维增强体中的气体，利用树脂的流动、渗透来实现浸渍纤维，并在室温下进行固化的加工工艺［8］。

在考虑资源循环利用、节能环保的基础上，作者以亚麻纤维为增强体制备了亚麻纤维增强环氧树脂基复合材料，研究了亚麻纤维体积分数对复合材料拉伸性能的影响；并在Kelly-Tyson拉伸强度预测模型及相关修正理论的基础上建立了该复合材料拉伸强度的预测模型，应用该模型对复合材料的拉伸强度进行了预测。

1 试样制备与试验方法

1.1 试样制备

试验用亚麻纤维的拉伸强度为420MPa，直径为80μm；试验用树脂为EPOLAM-5015型环氧树脂，呈浅琥珀色，其在25℃时的黏度为800mPa·s，25℃时密度为1.15g·cm-3。

采用真空辅助树脂传递模塑（VARTM）工艺制备亚麻纤维增强环氧树脂基复合材料。以七层尺寸为200mm×200mm×0.8mm的亚麻纤维布为增强体。试样制备前先将亚麻纤维布放入恒温干燥箱中（温度为50℃）干燥30min，干燥后亚麻纤维布的质量为80g。模具四周贴好密封胶带后，在密封胶带范围内涂覆脱模剂，将干燥后的亚麻纤维布置于模具内，亚麻纤维布上依次铺放脱模布和高渗透介质；然后用真空袋膜密封整个模具，密封后在真空袋膜两端开注胶口与出胶口，出胶口与树脂收集罐相连。配置树脂时，树脂与固化剂的质量比为100…34。计算所需树脂的质量为103g，适当多配少许，以保证树脂能始终浸没注胶管，搅拌均匀后于室温下静置一段时间，待树脂胶液变得十分清亮时，将其置于真空烘箱中抽真空以去除树脂内的气泡。对密封模具抽真空，待模具内压力达到0.02MPa时，保持在该真空度下，打开注胶口，让树脂进入模具，树脂浸润时间为45s。保持模具密封，将模具放入60℃的烘箱中加热2h。

1.2 试验方法

参考ASTM D3039／D3039M-00、GB 1447-1983和GB／T 1040-1992［9-11］，选取5个有效拉伸试样，采用CMT5504型万能力学试验机测复合材料的拉伸性能，拉伸速度设定为2mm·min-1，试样尺寸为120mm×20mm×4mm，试验环境温度为25℃，相对湿度为65%。

2 试验结果与讨论

由表1可见，当亚麻纤维的体积分数为38.6%时，复合材料的拉伸强度最大。对于亚麻纤维体积分数低于38.6%的复合材料而言，其拉伸强度较低的主要原因在于亚麻纤维的含量少，不能充分发挥增强作用；对于纤维体积分数高于38.6%的复合材料而言，其拉伸强度较低的主要原因在于过多的亚麻纤维致使树脂基体不能有效包覆粘合纤维，即材料的界面性能较差，从而导致高纤维含量复合材料的力学性能较低。

表1 不同体积分数亚麻纤维增强环氧树脂基复合材料的拉伸强度Tab.1 Tensile strength of different volume fraction flax fiber reinforced epoxy resin composite

3 拉伸强度预测模型的建立

3.1 模型修正

拉伸强度是复合材料重要的力学性能之一，它主要取决于树脂和增强纤维本身的力学性能以及纤维的体积分数、长度和取向分布。参考文献［12］报道的Kelly-Tyson拉伸强度预测模型中仅仅考虑了纤维体积分数对拉伸强度的影响。基于此，作者考虑了纤维取向角对拉伸强度的影响，并结合Fukuda［13］、Pipes［14］的取向因子理论、Sanomura［15］的取向因子整合理论，对Kelly-Tyson拉伸强度预测模型进行了修正，增加了纤维取向因子和纤维长度效应因子。植物纤维都是含有多种缺陷的，故在拉伸强度预测模型中又加入了对亚麻纤维特性的分析，植物纤维的单丝强度服从多重Weibull分布，通过Weibull分布理论可以确定亚麻纤维的拉伸强度，进而对复合材料的拉伸强度进行预测。

3.2 模型的建立

在Kelly-Tyson拉伸强度预测模型的基础上，建立了亚麻纤维增强环氧树脂基复合材料拉伸强度的预测模型，见式（1）。

σcu＝Cosη1sσfuφf＋σmu（1-φf） （1）

式中：σcu为亚麻纤维增强环氧树脂基复合材料的拉伸强度；σfu为纤维的拉伸强度；σmu为基体（环氧树脂）的拉伸强度，25MPa；φf为纤维的体积分数；Cos为反映纤维取向角分布对拉伸强度影响的取向因子；η1s为反映纤维长度分布对拉伸强度影响的长度效应因子。

3.3 拉伸强度的计算

取向因子Cos可以采用式（2）计算得到。

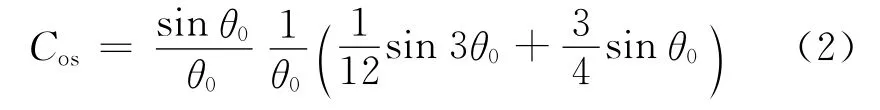
式中：θ0为纤维取向角分布中的临界角。

因复合材料较薄，所以在测试纤维取向角过程中将其视为二维，又因复合材料中纤维和基体的颜色可以较好地区分，因此在材料表面划定2cm×2cm的面积，统计纤维与受力方向的夹角。纤维取向角概率分布如图1所示，可以看出，取向角在0°～40°之间时纤维取向分布近似于矩形。

纤维取向角θ与取向分布中临界角θ0之间的关系式为：

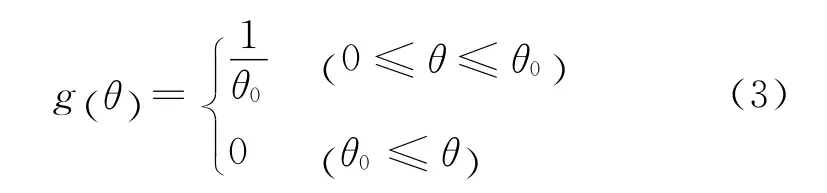
图1 亚麻纤维在复合材料中的取向角概率分布Fig.1 Probability distribution of orientation angle of flax fiber in the composite

为了计算Cos的值，需要求解出θ0的值，在计算θ0的过程中需要引入取向系数fp，其表达式为：

fp＝2〈cos2θ〉-1 （4）

〈cos2θ〉可以依据纤维取向角与取向分布中临界角之间的关系式确定，见式（5）。

根据图1所示的亚麻纤维在复合材料中的取向角概率分布及以上各式计算得出式（1）中的取向因子Cos为0.512。

式（1）中的长度效应因子η1s与纤维的临界长度lc之间具有一定的制约关系，见式（6）。

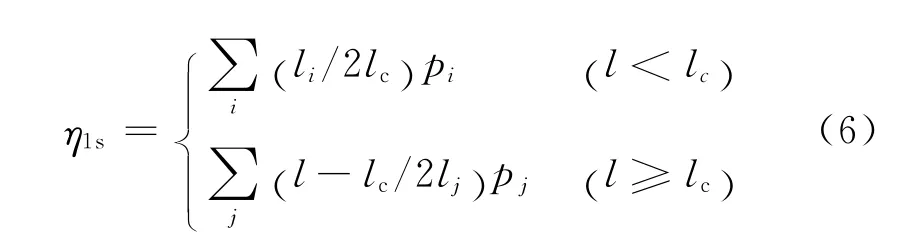
式中：i，j分别为大于及小于临界长度的纤维长度区间；pi，pj为长度分布频率；li和lj分别为大于和小于临界长度的纤维长度；l为纤维长度的测量值。

可通过测试梳理后纤维长度的概率分布确定式（6）中li，lj，pi，pj的值，具体的测试过程参考 GB 5887-1986。Kelly等［16］的研究表明，作为增强体的纤维存在着一个临界长度，当纤维的长度小于该临界长度时，应力无法传递到纤维上，纤维也就起不到增强的作用。试验制备的复合材料中纤维的临界长度lc为：

式中：df为根据纤维直径概率分布得出的纤维的平均直径，80μm；τs为复合材料界面的剪切强度。

纤维的拉伸强度σfu可根据式（8）计算得到。

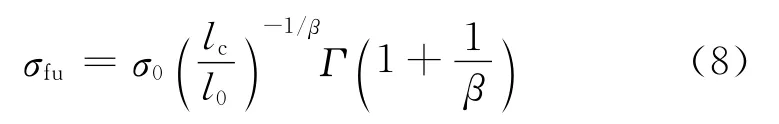
式中：σo为纤维强度 Weibull分布中的尺度参数；β为形状参数；l0为纤维长度的平均值。

形状参数是最重要的参数，决定分布密度曲线的基本形状；尺度参数起放大或缩小的作用，但不影响分布的形状。根据图2中亚麻纤维拉伸强度的数据采用最大似然法估计，可以计算得出σ0为320.02MPa，β为1.91。通过求解式（7）和式（8）最终可确定出σfu和lc的值，代入式（6）中即可求得ηls的值，即不同纤维含量的复合材料因界面剪切强度τs不同，其所对应的纤维的临界长度lc、纤维的拉伸强度σfu及纤维长度效应因子ηls均有所不同，它们的具体数值见表2。

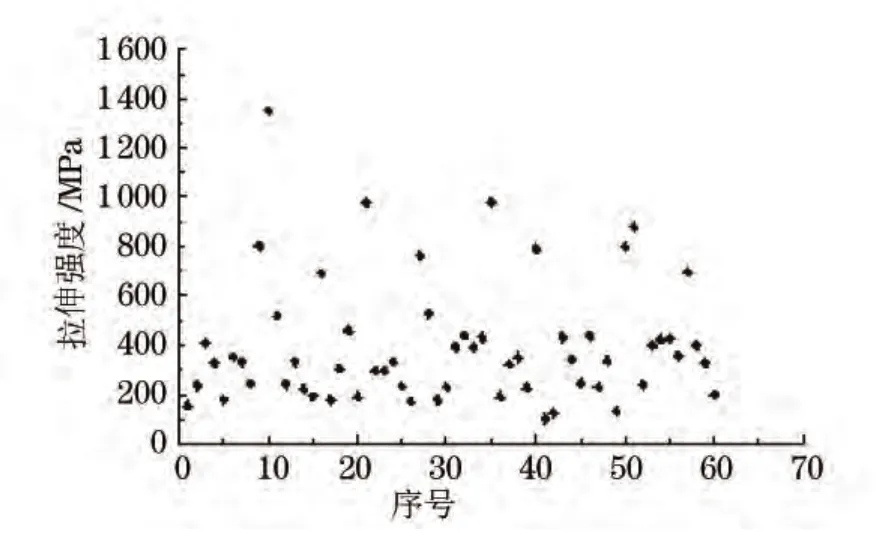
图2 亚麻纤维拉伸强度的概率分布Fig.2 Probability distribution of tensile strength of fibers

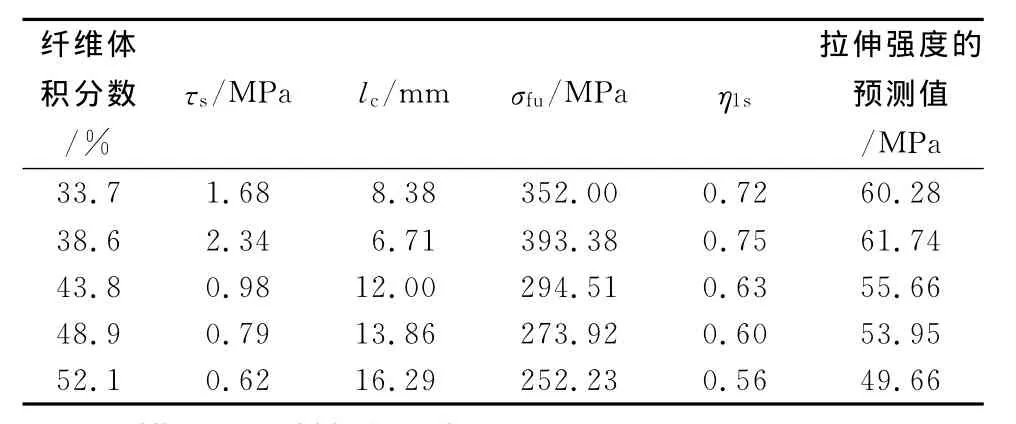
表2 拉伸强度预测模型中各参数的计算值Tab.2 Calculated value of parameters in the tensile strength prediction model

3.4 模型预测精度分析

为了定量表达拉伸强度预测模型的预测值与试验值之间的拟合程度，使用式（9）所示的预测精度p0对拟合程度进行表征。

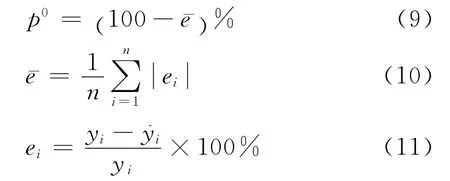
式中：yi，分别为拉伸强度的试验值和拟合值；ei为相对残差；为平均残差；n为试验次数。

根据表2中的数据以及式（9～11）可以计算得到亚麻纤维增强环氧树脂基复合材料拉伸强度预测模型的预测精度为97.8%。

4 结 论

（1）在Kelly-Tyson拉伸强度预测模型的基础上，考虑了纤维取向角对拉伸强度的影响，并加入了纤维取向因子和纤维长度效应因子，建立了修订后的亚麻纤维增强环氧树脂基复合材料拉伸强度的预测模型。

（2）不同纤维含量的复合材料因界面剪切强度不同，其所对应的纤维的临界长度、纤维的拉伸强度及纤维长度效应因子均有所不同。

（3）当纤维的体积分数为38.6%时，复合材料的拉伸强度最大，约为63.10MPa；低于该纤维含量时，亚麻纤维因不能充分发挥增强作用而使复合材料的拉伸强度降低，高于该纤维含量时，因复合材料的界面性能较差而导致拉伸强度降低。

（4）新建立的拉伸强度预测模型的预测精度约为97.8%。

［1］ROUISONA D，SAINB M，COUTURIERA M.Resin transfer molding of natural fiber reinforced composites：cure simulation［J］.Compos Sci Technol，2004，64：629-644.

［2］AZIZ S H，ANSELL M P，CLARKE S J，et al.Modified polyester resins for natural fiber composites［J］.Compos Sci Technol，2005，65：525-535.

［3］FENG D，CAULFIELD D F，SANADI A R.Effect of compatibilizer on the structure-property relationships of kenaffiber／polypropylene composites［J］.Polym Compos，2001，22：506-517.

［4］张赋，李旭东.织物增强复合材料弹性常数的有限元法预测［J］.机械工程材料，2014，38（4）：82-86，95.

［5］才红.表面处理方法对剑麻纤维／酚醛树脂复合材料性能的影响［J］.机械工程材料，2010，34（3）：15-18.

［6］杨敏鸽，王琼，秦辉，等.苎麻增强环氧树脂复合材料的力学性能［J］.机械工程材料，2012，36（6）：68-71.

［7］李小慧，金石磊，孙斓珲，等.聚酯纤维布增强环氧树脂基复合材料的拉伸和摩擦学性能［J］.机械工程材料，2010，34（3）：61-65，69.

［8］郭明恩，孙祖莉，李 峻，等.真空导入树脂模塑工艺对EKB1100／430LV复合材料纤维含量及力学性能的影响［J］.机械工程材料，2012，36（5）：38-41.

［9］ASTM.D3039／D3039M-00Standard test method for tensile properties of polymer matrix composite material［S］.

［10］GB 1447-1983玻璃纤维增强塑料拉伸性能试验方法［S］.

［11］GB 3357-1982单向纤维增强塑料层间剪切强度试验方法［S］.

［12］GARKHAIL S K，HEIJENRATH R W H，PEIJS T.Mechanical properties of natural-fibre-mat-reinforced thermoplastics based on flax fibres and polypropylene［J］.Applied Composite Materials，2000，7（5／6）：351-372.

［13］FUKUDA H，CHOU T W.A probabilistic theory of the strength of short-fiber composites with variable fiber length and orientation［J］.Journal of Material Science，1982，17：1003-1011.

［14］PIPES R B.MCCULLOUGH R L，TAGGART G.Behavior of discontinuous fiber composites：fiber orientation［J］.Polymer Composite，1982，3（1）：34-37.

［15］SANOMURA Y，HAYAKAWA K，MIZUNO M.Effects of process conditions on Young′s modulus and strength of extrudate inshort-fiber-reinforced polypropylene［J］.Polym Compos，2007，28（1）：29-35.

［16］KELLY A，TYSON W R.Tensile properties of fibre-Reinforced metals：copper／tungsten and copper／molybdenum［J］.J Mech Phys Solids，1965，13：329-338.