硬质聚氨酯泡沫材料的常温蠕变特性

魏 轩，赵 华

（西南交通大学力学与工程学院，成都610031）

0 引 言

随着金属、橡胶、复合材料的广泛应用，这些材料粘弹性力学行为的研究受到了广泛关注［1-4］，而蠕变能最为直观地表现了材料的粘弹性能。大多数高聚物材料都具有尺寸稳定性差的缺点，在常温下就会发生较大的蠕变变形，最终导致材料破坏，这大大降低了材料的稳定性和可靠性，影响其在工业领域的应用。许多学者［5-8］研究了粘弹塑性材料的蠕变行为，结果发现，蠕变对应力、温度和组织结构等具有很强的依赖性。硬质聚氨酯泡沫材料与橡胶一样，是一种粘弹性材料，由于其刚度高，密度小，隔热、吸声、减振性能好，近年来广泛应用于航空、国防、汽车等领域，例如制造运送液化石油气的船舱、导弹顶级上的隔舱壁板以及建筑物的吊顶面板等［9］。但相对于国外规模化的应用而言，国内还处于起步阶段。为充分利用聚氨酯泡沫材料的性能优点进行产品结构设计，对其蠕变性能进行研究是十分必要的。

描述粘弹性材料蠕变行为的模型有很多，如Kelvin模型、Poynting-Thomson模型、Findley幂律模型等［10-13］，但绝大多数模型只适用于材料的拉伸蠕变；而且，目前所查资料对于硬质聚氨酯泡沫材料的基本力学性能，特别是压缩蠕变特性鲜有报道。在众多模型中，Burgers模型的参数较少，并且能够较好地反映高分子材料在不同应力下的蠕变过程，因此在实际中得到了一定应用。为了获得硬质聚氨酯泡沫材料在不同载荷水平下的蠕变行为，作者在常温、不同应力水平下其进行单轴蠕变压缩试验，并在试验的基础上，利用Origin8.0软件对Burgers模型参数进行拟合，计算出了蠕变模型中弹簧的弹性模量和粘壶的粘性系数，得到了硬质聚氨酯泡沫材料蠕变柔量的表达式和蠕变本构方程，并将试验得到的蠕变曲线和计算得到的蠕变曲线进行了对比，以验证蠕变模型的准确性。

1 粘弹性材料的蠕变特性及模型

Burgers模型可以看作是由Maxwell模型和Kelvin模型串联而成的，如图1所示。

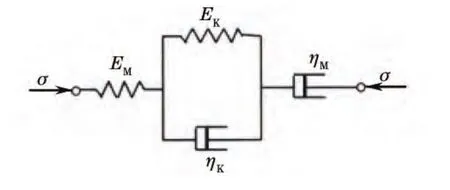
图1 Burgers模型Fig.1 Burgers model

Burgers模型是根据高分子的运动机理设计的。高聚物的形变由三部分组成：第一部分为瞬时完成的普弹形变，用一个弹性模量为EM的弹簧来模拟；第二部分为随时间变化的高弹形变，用弹性模量为EK的弹簧和粘性系数为ηK的粘壶并联起来模拟；第三部分为随时间线性发展的粘性流动，用一个粘性系数为ηM的粘壶来模拟。高聚物的整体形变为这三部分形变的总和，因此模型的这三部分元件应该串联起来。假设高聚物材料蠕变时的应力σ＝σ0＝常数，则高聚物的整体应变和时间的关系为：

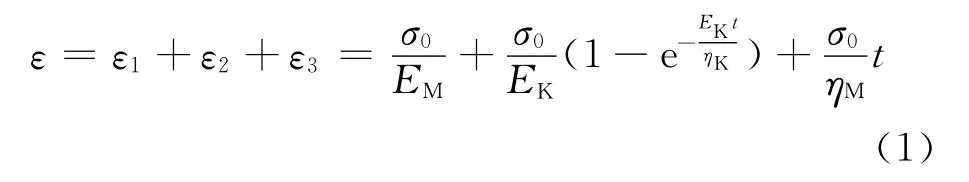
式中：σ0为加载应力；ε为应变；ε1，ε2，ε3分别为高聚物形变三个组成部分的变形；t为时间。

在给定应力的情况下，代入不同的时间t即可得到一条蠕变曲线。通过将计算得到的蠕变曲线与试验得到的蠕变曲线进行对比，即可证明该模型的正确性。

改写式（1），得到蠕变柔量的表达式为：

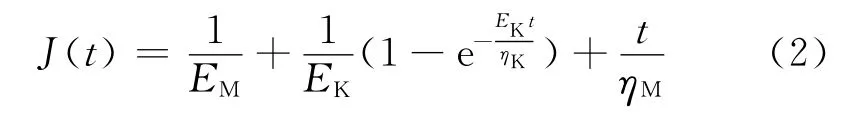
式中：J 为蠕变柔量，J＝ε／σ0；ηK／EK为松弛时间，记作τ。

需要指出的是，尽管增加Maxwell元件数量可以提高模型的精度，但会给提取模型参数带来很大困难，因此元件数量只要满足工程需要即可［14］。

2 试验方法与结果

试验采用某厂提供的牌号为江淮946的特制各向同性硬质聚氨酯粘弹性泡沫材料，其弹性模量为175MPa，泊松比为0.433，密度为0.37g·cm-3。经打磨加工后得到尺寸为6mm×6mm×17mm的长方体试样。

采用WDW3100型微机控制电子万能试验机对硬质聚氨酯泡沫材料进行单轴压缩试验，压缩速度为1mm·min-1，通过载荷-位移曲线可知其屈服强度为4.314 1MPa，因此试验选取的五个蠕变应力分别为1.495 2，2.254 4，2.654 1，3.808 3，4.097 1MPa。采用分别加载的方式对硬质聚氨酯泡沫材料进行单轴压缩蠕变试验，试验环境为常温。在试验过程中，一边记录试验数据，一边记录压缩变形量随时间的变化，并绘制蠕变曲线。

从图2可以看出，硬质聚氨酯泡沫材料的压缩蠕变曲线呈现出明显的非线性特征；在施加载荷的瞬间，材料的响应主要是弹性变形，服从胡克定律；随着应力增大，瞬间弹性变形逐步增大，在3.808 3MPa应 力 下，瞬时弹性应变较2.254 4MPa应力下高出一倍左右。高弹形变反映了受载后蠕变形变随时间延长而增大的关系，总体来讲，随着应力增大，硬质聚氨酯泡沫材料的高弹形变也增大。粘性流动变形是材料在蠕变过程中随时间延长而线性变化的永久变形，这种不可恢复的变形是由于材料发生了不可逆的塑性流动，并随应力和作用时间的增加而增加。

图2 硬质聚氨酯泡沫材料在不同应力下的蠕变曲线Fig.2 Creep curves of hard polyurethane foam at different stresses

从图2还可以看出，硬质聚氨酯泡沫材料在获得初始应变后，应变快速增大，达到某一值后增速变慢，大约经过50h以后，蠕变速率逐渐减小到一个稳定值，此时应变的波动范围很小，并随时间延长而呈线性增加；随着应力增大，蠕变曲线变陡，这说明蠕变速率随应力增大而增大。

从表1可以看出，硬质聚氨酯泡沫材料压缩蠕变量受应力的影响较大，即应力越大，蠕变变形量越大。

表1 不同应力下硬质聚氨酯泡沫材料蠕变200h后的蠕变变形量Tab.1 Creep strain of hard polyurethane foam after creep at different stresses for 200h

3 Burgers模型参数拟合

用式（1）对不同应力下的压缩蠕变试验数据进行非线性拟合，可得到Burgers模型中的材料参数，如表2所示。可见在不同应力下，拟合曲线与蠕变曲线的相关系数R2均大于0.97，这说明拟合结果与试验结果具有较好的一致性，Burgers模型可以较为准确地模拟硬质聚氨酯泡沫材料的压缩蠕变行为。

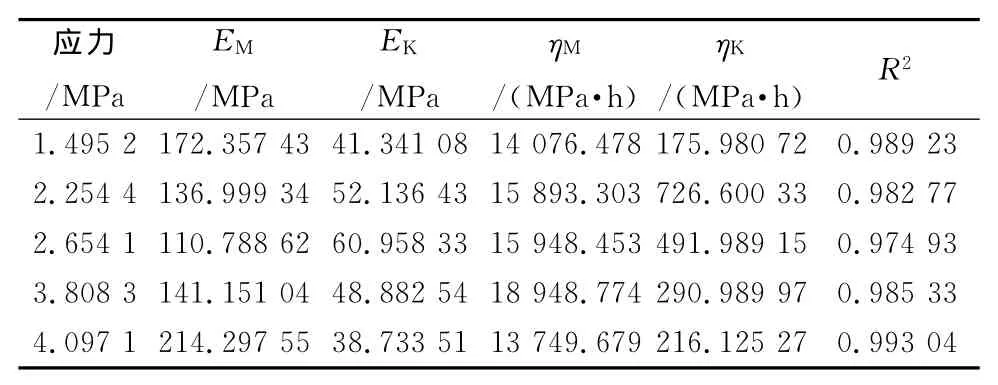
表2 不同应力下硬质聚氨酯泡沫材料蠕变数据回归分析结果Tab.2 Regression analysis results of creep data of hard polyurethane foam at different stresses

表2中的参数都是具有应力相关性的。如，随着应力增大，硬质聚氨酯泡沫材料的普弹形变有降低的趋势，这是由于突加载荷引起的弹性应变。将这些参数代入到式（1）中即可得到材料在不同应力下的一维本构方程。但在实际应用中，往往希望得到某一应力下的压缩蠕变曲线。通过对以上数据进行插值可以得到一个更为普遍的、适用于各种应力的材料参数。具体方法如下。

根据试验数据做出硬质聚氨酯泡沫材料的应变-应力等时曲线，如图3所示。

图3 硬质聚氨酯泡沫材料蠕变不同时间后的应变-应力等时曲线Fig.3 Strain-stress isochronous curves of hard polyurethane foam after creep different times

从图3可以看出，应变与应力的比值（即蠕变柔量）随时间延长而增大。对图3中每组应变-应力等时曲线做通过（0，0）点的线性拟合，所得直线的斜率即为该时刻硬质聚氨酯泡沫材料的蠕变柔量。以时间t为横坐标，J（t）为纵坐标，作散点图，然后利用Origin8.0的自定义函数拟合功能，将Burgers模型的蠕变柔量方程编入软件中，并对试验数据进行非线性拟合回归，蠕变柔量拟合曲线如图4所示。拟合曲线与蠕变柔量曲线的相关系数为0.998 28，说明Burgers模型可以较为准确地模拟硬质聚氨酯泡沫材料的压缩蠕变行为。模型参数拟合结果如表3所示。

把参数拟合结果代入式（1）可得硬质聚氨酯泡沫材料的压缩蠕变本构关系为：

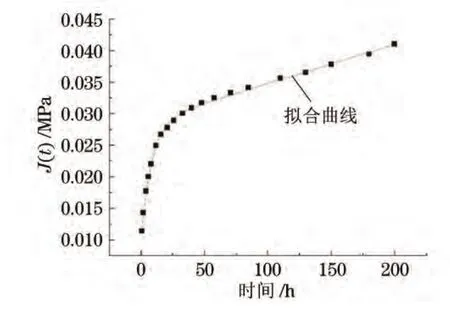
图4 硬质聚氨酯泡沫材料蠕变柔量的拟合曲线Fig.4 Fitted curve of creep compliance of hard polyurethane foam

表3 Burgers模型中参数的拟合结果Tab.3 Fitted results of parameters in Burgers model

4 蠕变模型的试验验证

选取1.298 6MPa应力，采用同样的方法对硬质聚氨酯泡沫材料在常温下进行压缩蠕变试验，并将试验所得蠕变曲线与蠕变模型预测结果进行比较。由图5可以看出，模型预测结果与蠕变试验得到的蠕变曲线具有相同的趋势，最大误差在10%以内。这说明利用Burgers模型模拟硬质聚氨酯泡沫材料的压缩蠕变过程是较为合理可行的。

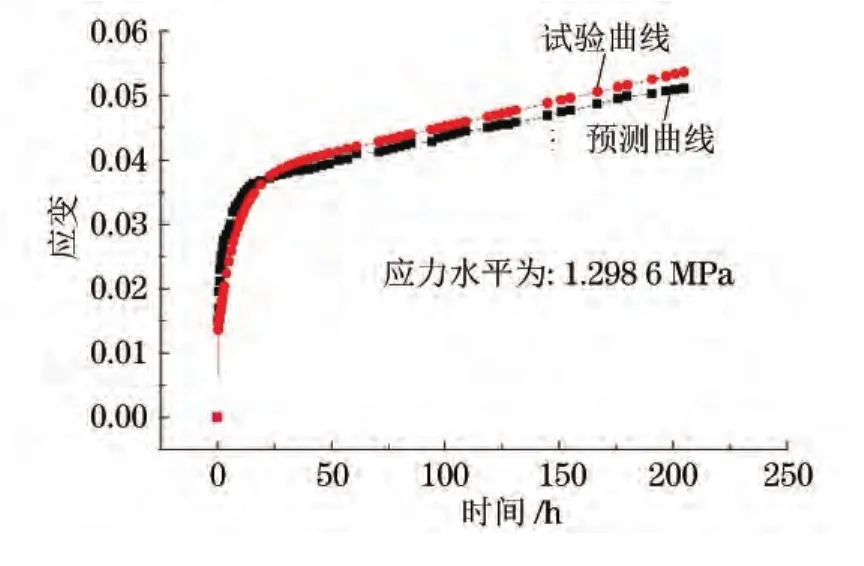
图5 蠕变模型预测结果与试验得到的蠕变曲线对比Fig.5 Comparison of creep model predicted results and experimental creep curves

由图6可见，在1.298 6MPa应力水平下，硬质聚氨酯泡沫材料的压缩蠕变行为表现为典型的两个阶段。第一阶段在瞬间获得初始应变以后，应变快速增加，蠕变速率逐渐减小，称为减速蠕变阶段；当蠕变速率减小到一个稳定值时，蠕变进入第二阶段，蠕变应变随时间延长呈线性增加，蠕变速率基本保持不变。

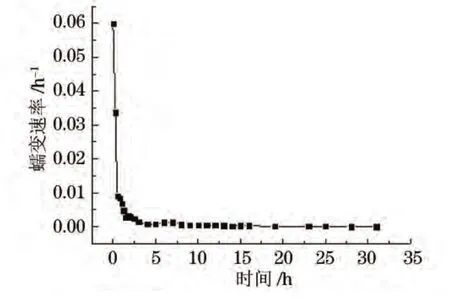
图6 1.298 6MPa应力下硬质聚氨酯泡沫材料压缩蠕变速率随时间的变化曲线Fig.6 Compression creep rate vs time for hard polyurethane foam at 1.298 6MPa stress

稳态蠕变速率的大小除了取决于材料的化学成分、组织结构等固有特性外，还与温度和应力这两个外部变量有关。对硬质聚氨酯泡沫材料压缩蠕变试验数据进行拟合，即可得到其在稳态蠕变第二阶段的蠕变速率。

对硬质聚氨酯泡沫材料压缩蠕变本构关系式求导，可得到其在压缩蠕变第二阶段的稳态蠕变速率为：

经过足够长的时间后，材料的蠕变速率接近于恒定值：

把蠕变本构方程参数和应力值代入式（5），可得到不同应力水平下经过足够长时间后的稳态蠕变速率。

蠕变试验测得的蠕变速率和蠕变模型预测的蠕变速率如表4所示。

表4 硬质聚氨酯泡沫材料蠕变速率的试验值与模型预测值Tab.4 Experimental values and model prediction value of creep rate of hard polyurethane foam

由表4可知，在3.808 3MPa应力下，硬质聚氨酯泡沫材料蠕变速率的试验值与模型预测值相差较大，推测是由材料加工或存放等原因引起的；在其它应力下，蠕变速率的试验值和模型预测值基本一致。可见，由Burgers模型导出的蠕变速率公式可以很好地预测硬质聚氨酯泡沫材料压缩蠕变第二阶段的蠕变速率。

5 结 论

（1）常温下，硬质聚氨酯泡沫材料的压缩蠕变曲线可分为两个阶段，第一阶段的蠕变速率随时间延长而逐渐降低，第二阶段的蠕变速率基本保持恒定。

（2）常温下，硬质聚氨酯泡沫材料的压缩蠕变行为有明显的应力相关性，随着加载应力增大，蠕变变形量和稳态蠕变速率均增大。

（3）Burgers模型可以用于预测硬质聚氨酯泡沫材料的常温蠕变行为，而且拟合效果良好。

（4）Burgers模型导出的稳态蠕变速率公式可以较好地预测聚氨酯材料在压缩稳态蠕变阶段的蠕变速率。

［1］周光全，刘孝敏.粘弹性理论［M］.合肥：中国科技大学出版社，1996：1-20.

［2］ZHANG Yun，HUANG Zhu-ping.Void growth and cavitation in nonlinear viscoelastic solids［J］.Acta Mechanica Sinica，2003，19（4）：380-384.

［3］杨挺青.粘弹塑性本构理论及应用［J］.力学进展，1992，22（1）：10-19.

［4］YE Y ，YANG X H ，CHEN C Y.Experimental researches on visco-elastoplastic constitutive model of asphalt mastic［J］.Construction and Building Materials，2009，23（4）：3161-3165.

［5］董智贤.聚丙烯木塑复合材料蠕变行为的模拟与预测［J］.高分子材料科学与工程，2010，26（5）：89-96.

［6］谢苏江，蔡仁良.压缩非石棉密封板材蠕变松弛性能的理论和试验研究［J］.机械工程材料，2004，28（6）：14-16.

［7］黄硕，万敏，黄霖，等.铝合金蠕变试验及本构模型建立［J］.航空材料学报，2008，28（1）：93-96.

［8］张姝，田素贵，钱本江，等.单晶镍基合金在拉伸蠕变期间的组织演化与分析［J］.稀有金属材料与工程，2012，41（1）：28-32.

［9］郝松林，孙卫明，屈明，等.硬质聚氨酯泡沫塑料的粘弹性［J］.高分子材料科学与工程，1997，13（6）：77-81.

［10］董自虎，孙吉.船用高分子材料压缩蠕变特性研究［J］.材料开发与应用，2004（6）：76-80.

［11］潘颖，丁雁生，蔡瑞娇.PBX聚合物基复合材料蠕变损伤一维模型［J］.兵工学报，2002（2）：123-127.

［12］康永刚，张秀娥.修正的高分子材料蠕变模型［J］.材料科学与工程学报，2013，31（6）：924-928.

［13］谢苏江，蔡仁良.非石棉短纤维增强橡胶密封材料蠕变的理论和试验研究［J］.橡胶工业，2002，49（4）：205-209.

［14］束立红，何琳.聚氨酯隔振器蠕变特性力学模型试验研究［J］.噪声与振动控制，2012，4（2）：147-150.