弹丸质偏对引信解除保险距离的影响

张　健，李作华，侯小丫，曲凡军

(1.海军驻沈阳弹药专业代表室，辽宁 沈阳 110045；2.辽宁华兴机电有限公司，辽宁 锦州 121000；

3.辽沈工业集团有限公司，辽宁 沈阳 110045)



弹丸质偏对引信解除保险距离的影响

张健1，李作华2，侯小丫2，曲凡军3

(1.海军驻沈阳弹药专业代表室，辽宁 沈阳 110045；2.辽宁华兴机电有限公司，辽宁 锦州 121000；

3.辽沈工业集团有限公司，辽宁 沈阳 110045)

摘要：为揭示弹丸存在质量偏心时对引信无返回力矩钟表机构解除保险距离的影响，建立动力学模型，结合产品实例，利用Matlab软件分析弹丸质偏变动所引起的解除保险距离变化情况。结果证明，弹丸存在质偏时会引起引信解除保险距离的散布，引信设计时需考虑弹丸质偏对引信解除保险距离的影响，弹药生产过程也需对弹丸质偏加以控制，以便为引信可靠作用提供适宜条件，有效发挥弹药的毁伤效能。

关键词：弹丸；质偏；引信；保险距离

引信的延期解除保险距离是保证弹药在发射器附近人员与设施安全性的一项重要性能参数[1-2]。无返回力矩钟表机构是引信系统中一种非常重要的延期解除保险机构[3]。一般包括原动机、齿轮系和调速器(骑马轮、卡瓦摆)等三部分，被保险的零件或机构(例如装有雷管的转子)固连在驱动齿轮或齿条上，驱动力矩由弹簧(多为扭簧)或弹丸运动时的惯性力来产生。利用弹丸旋转环境产生的离心力作为原动力驱动钟表机构运转，是旋转弹引信钟表延期解除保险装置非常适宜的方式。这种机构合理利用了弹丸飞行环境，避开了储能设计；利用导程与弹径的比例关系(火炮缠度)，调节不同弹径所要达到的解除保险距离。

在外弹道上，弹丸的质偏会引起弹丸旋转轴线与引信钟表保险机构的几何中心轴线发生随机偏移,这种偏移会改变钟表机构的驱动力矩和摩擦力矩，影响保险机构解除保险距离。本文研究弹丸质偏对钟表机构解除保险距离的影响。

1　无返回力矩钟表机构动力学模型

根据弹药的发射特性，引信采用带离心齿弧的回转体和无返回力矩钟表组成[4]的自适应钟表延期解除保险机构实现平时安全与发射后可靠解保。为分析钟表延期解除保险机构的延期性能，建立动力学模型(不考虑偏摆现象)。

1) 骑马轮的导出转动惯量

IR/(N3N2N1)2

(1)

式中：I1为第一轮转动惯量；I2为第二轮转动惯量；IE为骑马轮转动惯量；IR为转子转动惯量；N1为首级传动比；N2为次级传动比；N3为三级传动比。

摩擦力矩等效因子

f=mRrrPR+(N1/η)m1r1rP1+(N1N2/η2)m2r2rP2+(N1N2N3/η3)mqrqrpq+

(N1N2N3PKp/η4)mbrbrpb

(2)

式中：mR为转子质量；r为转子轴与旋转轴距；P为擒纵运动系数；Kp为擒纵机构力矩传动比；rPR为转子轴半径；rP1为第一轮轴半径；rP2为第二轮轴半径；rPq为骑马轮轴半径、rPb为摆轴半径；r1为第一轮与旋转轴距；r2为第二轮与旋转轴距；rq为骑马轮与旋转轴距；rb为摆轴与旋转轴距；为传动效率。

擒纵机构导出传动比

(3)

Ie由式(1)求得；Ip为摆转动惯量。

钟表机构导出传动比

Cn=CE(N3N2N1)3/η3

(4)

平均剩余驱动力矩

D=mRarη4(cosθ0-cosθ1)/(θ1-θ0)-μf

(5)

式中：a为转子偏心距；θ0为转子起始角；θ1为解除保险角；μ为摩擦系数；f可由式(2)求得。

钟表延期解除保险机构的特征值

N=(θ1-θ0)(Cn/D)0.5

(6)

2) 钟表机构延期解除保险距离计算

钟表延期解除保险机构实现弹药平时安全与发射后可靠解保险，发射后的延期保险距离与弹丸的弹径、火炮缠度和钟表延期解除保险机构特征参数三个元素乘积成正比，延期保险距离计算公式如下。

S=N·Dh·m

(7)

式中：Dh为弹丸直径；m为火炮缠度；N为钟表延期解除保险机构的特征值。

对于一种弹药系统来说，弹丸直径、火炮缠度参数不变，影响弹药的延期保险距离只有钟表延期解除保险机构的特征参数。

2　钟表延期解除保险机构实例

图1为某型钟表延期解除保险的一个实例，设计参数见表1。

理想状态延期解除保险特征参数：N=32r，对应122毫米榴弹炮的解除保险距离为78m。

3　弹丸质偏对解保距离影响的计算

以配用于122毫米榴弹炮引信为例，利用Matlab软件计算弹丸质心轴偏移量分别为1mm、2mm、5.52mm、5.55mm和质心轴偏转角对解除保险距离的影响情况。解除保险距离与弹丸质心轴偏角的关系如图2～图5(偏角θ为转子轴、钟表机构中心轴、弹丸质心轴之间形成的夹角)。

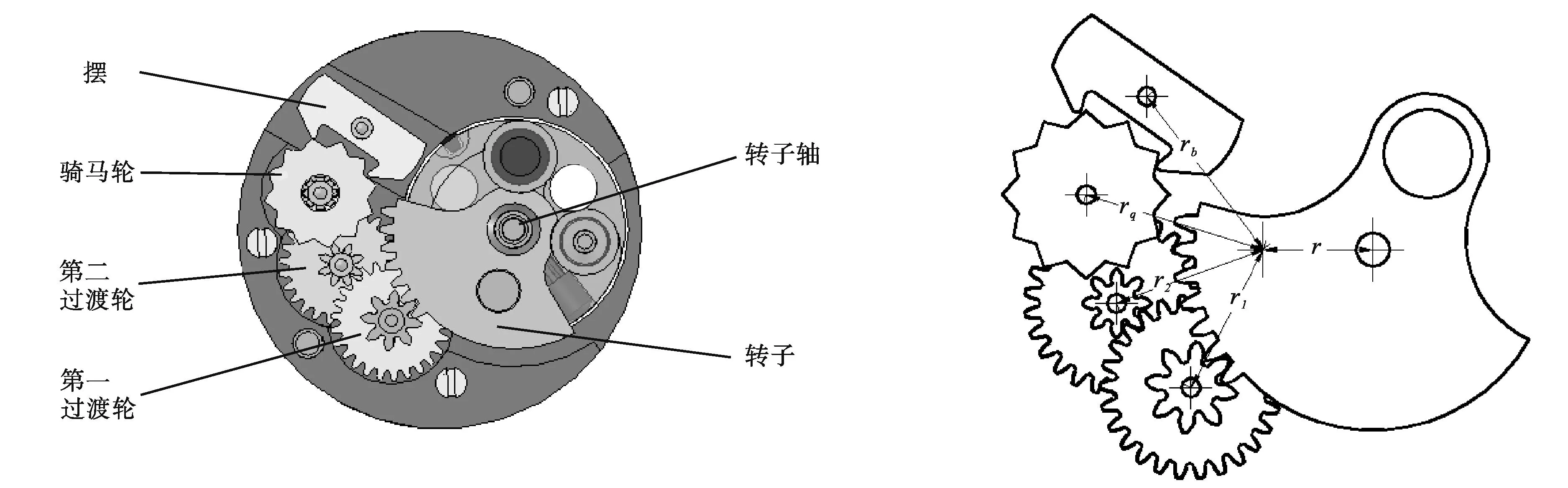
图1　钟表机构示意图

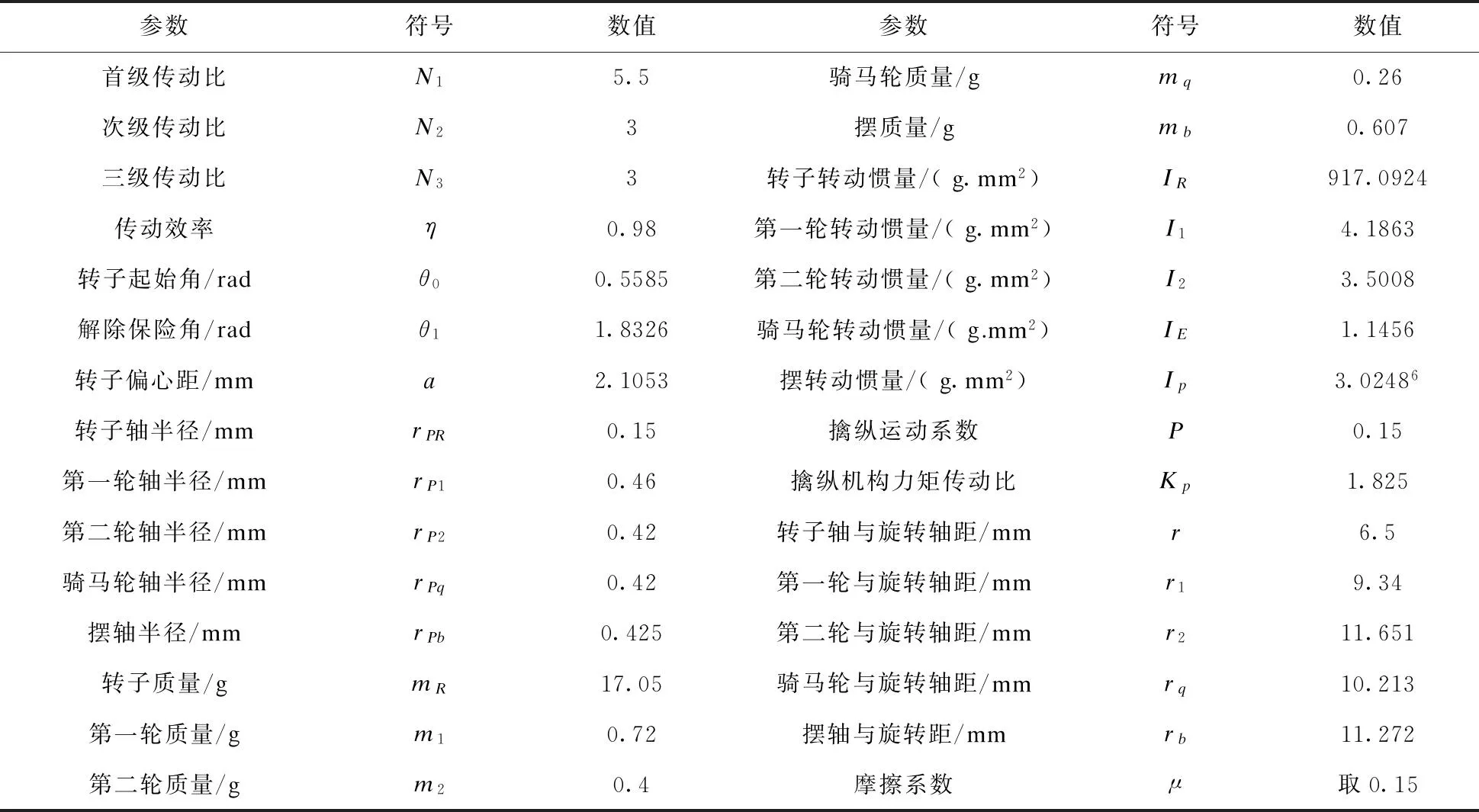
参数符号数值参数符号数值首级传动比N15.5骑马轮质量/gmq0.26次级传动比N23摆质量/gmb0.607三级传动比N33转子转动惯量/(g.mm2)IR917.0924传动效率η0.98第一轮转动惯量/(g.mm2)I14.1863转子起始角/radθ00.5585第二轮转动惯量/(g.mm2)I23.5008解除保险角/radθ11.8326骑马轮转动惯量/(g.mm2)IE1.1456转子偏心距/mma2.1053摆转动惯量/(g.mm2)Ip3.02486转子轴半径/mmrPR0.15擒纵运动系数P0.15第一轮轴半径/mmrP10.46擒纵机构力矩传动比Kp1.825第二轮轴半径/mmrP20.42转子轴与旋转轴距/mmr6.5骑马轮轴半径/mmrPq0.42第一轮与旋转轴距/mmr19.34摆轴半径/mmrPb0.425第二轮与旋转轴距/mmr211.651转子质量/gmR17.05骑马轮与旋转轴距/mmrq10.213第一轮质量/gm10.72摆轴与旋转距/mmrb11.272第二轮质量/gm20.4摩擦系数μ取0.15

从图2～5的曲线可以看出：1)质心轴偏移量为1mm:偏移角为1.64rad(94°)时解除保险距离出现最大值为82m；偏移角为4.32rad(248°)时解除保险距离出现最小值为76m2)质心轴偏移量为2mm:偏移角为1.80rad(103°)时解除保险距离出现最大值为88m；偏移角为3.82rad(219°)时解除保险距离出现最小值为75m3)质心轴偏移量为5.52mm:偏移角为2.54rad(146°)时解除保险距离达到3486m，远大于解除保险距离指标的上限；再增大质心轴偏移量(图5)，出现曲线断开现象，断开部分是解除保险距离无限长的状态，在此情况下，保险机构不能正常解除保险。

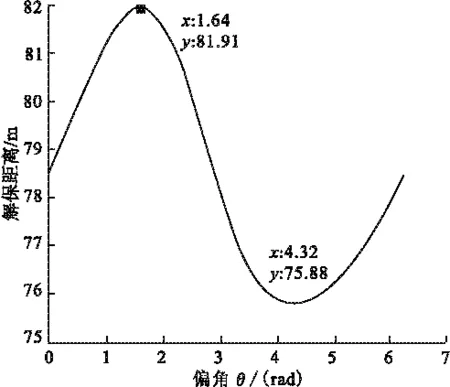
图2　轴偏1mm时解除保险距离曲线

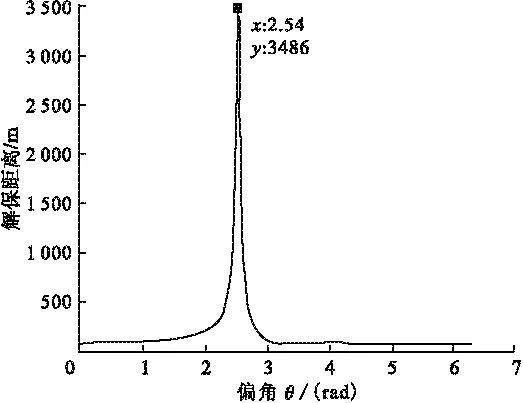
图3　轴偏5.52mm时解除保险距离曲线

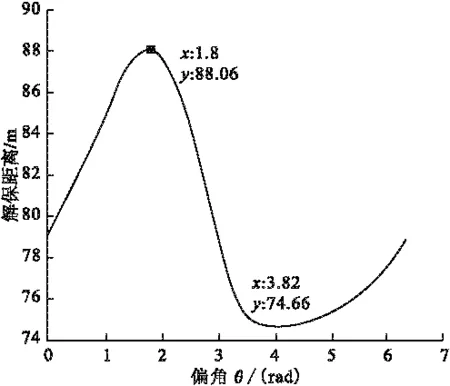
图4　轴偏2mm时解除保险距离曲线

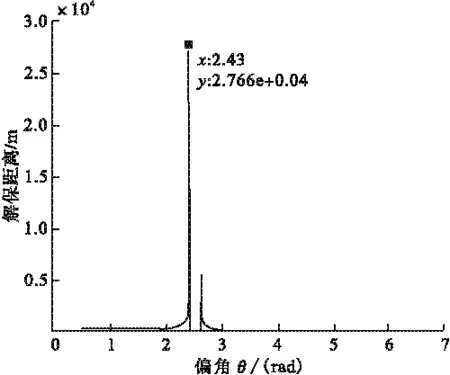
图5　轴偏5.55mm时解除保险距离曲线

4　结束语

弹丸的旋转轴线与引信钟表机构的几何轴线偏离时，会带来引信解除保险距离产生散布；在引信设计过程，需要考虑解除保险距离受轴向偏移所带来的影响，避免超出解除保险距离指标规定；在考核、验证引信解除保险距离时，应该控制所用惰性装填物试验弹(砂弹)的物理状态，使其与实弹一致或接近，以便反映产品实际特性；合理控制弹药质偏因素(壁厚差、战斗部装药均匀性等实物质量状态)，为引信功能与性能的正常发挥和实现提供适宜的环境条件。

参考文献：

[1]田棣华，马宝华，范宁军.兵器科学技术总论[M].北京：北京理工大学出版社，2003.

[2]王儒策，赵国志，杨绍卿.弹药工程[M].北京：北京理工大学出版社，2002.

[3]陆文广,芮筱亭,陆毓麒，等.无返回力矩钟表机构动力学研究[J].兵工学报，2005,26(3)：401-404.

[4]张合，李豪杰.引信机构学[M].北京：北京理工大学出版社，2007.

(责任编辑：赵丽琴)

Influence of Centroidal Deviation of Projectile on Unarming Distance of Fuze

ZHANG Jian1,LI Zuohua2,HOU Xiaoya2,QU Fanjun3

(1.Navy Permanent In Shengyang,Shenyang 110045,China；

2.Liaoning Huaxing Electrical Co.Ltd,Jinzhou 121000,China;

3.Liaoshen Industries Croup Co.Ltd,Shenyang 110045,China)

Abstract：In order to reveal the influence of mass centroidal deviation of projectile on fuze unarming diatance device of no return torque clock,proposes a kinetic model combined with real product samples and analyzes the unarming distance changes caused by changes of projectile mass deviation using Matlab software.Proves that if of projectile mass deviation occurs,the fuze unarming distance dispersion will be caused and so you should consider the affection when you design fuzes and slso should control the projectile mass deviation during ammunition production to provide suitablie conditions for fuze reliability functions and release the ammunition damaging performance.

Key words：projectile；eccentricity；fuze；unarming distance

中图分类号：TJ430

文献标志码：A

文章编号：1003-1251(2015)01-0013-04

作者简介：张健(1970—)，男，高级工程师，研究方向：弹药工程.

收稿日期：2014-04-28