某大口径枪械弹丸挤进坡膛过程的仿真分析

安俊斌，李 强，李世康，谭 庆

(中北大学 机电工程学院，山西 太原 030051)

某大口径枪械弹丸挤进坡膛过程的仿真分析

安俊斌，李 强，李世康，谭 庆

(中北大学 机电工程学院，山西 太原 030051)

针对目前理论和试验难以解决的三层结构的钢心弹丸在挤进枪管过程中的应力、转速和摆动问题，以某大口径枪械弹丸挤进过程为例，建立了弹丸和枪管的有限元模型，使用Johnson-Cook材料本构关系，运用动力显式方法对弹丸挤进过程进行了模拟，得到了弹丸的挤进阻力，展现了弹丸被甲表面刻痕的成形过程，研究了弹丸的应力情况和转速，并分析了弹丸在挤进过程中的摆动状况。分析结果可为优化坡膛结构，在满足武器要求的前提下改进弹丸形状以提高弹丸的稳定性提供理论参考依据。

枪管; 弹丸挤进; 有限元法; 弹丸变形

枪械发射过程包含弹丸挤进坡膛的过程，而弹丸挤进坡膛过程极其复杂，枪械击发后，膛内火药燃气压力不断上升，弹丸被甲逐渐嵌入膛线，产生塑性变形，弹丸加速运动，直至弹丸完全挤进坡膛。挤进过程分别涉及：材料非线性，弹丸被甲的大变形和失效问题；边界非线性，弹丸被甲与内膛接触问题；几何非线性，弹丸被甲的位移与旋转问题。在极短的时间和位移下，用实验方法模拟弹丸在高速变化的火药燃气压力作用下挤入坡膛，较为困难。经典内弹道通常假设挤进过程瞬间完成，不考虑弹丸挤进的影响，忽略了弹丸挤进过程[1-2]。然而挤进过程对弹丸膛内运动有很大影响，这就使得对弹丸挤进过程进行仿真显得十分必要。

何勇[3-4]最早提出了弹丸挤进过程的一维模型，通过静态实验和动态实验对弹丸挤进过程进行了研究，获得了一些实验数据，提供了一种技术方法。孙河洋等[5]利用MSC.Dytran软件模拟大口径火炮弹带挤进过程，分析了挤进过程中弹带、身管和膛线的应力及其变化规律，及弹丸受力与加速度的变化规律。樊黎霞等[6]通过数值模拟方法研究了铅芯弹头的挤进过程，分析了弹头壳和铅芯的变形特征，及挤进结束后弹头的残余应力。陆野等[7]采用多软件综合仿真的方法模拟弹丸的挤进过程，得到了弹丸嵌入阻力变化规律。

当前针对弹丸挤进过程研究大多对弹丸结构进行了简化，不能真实反映弹丸结构对挤进过程的影响。因3层结构弹丸在挤进过程中，变形过程和各层间相互作用复杂，挤进阻力求解有一定困难。现有研究往往不考虑弹丸在挤进过程中的摆动情况，与实际射击状况不相符合。笔者以某钢心3层结构弹丸挤进过程为研究对象，分析了挤进过程枪管受力情况，建立了仿真模型，得到了弹丸挤进阻力变化规律，分析了弹丸的应力和转速，并研究了弹丸在挤进过程中的摆动情况。

1 弹丸挤进过程理论分析

1.1 挤进过程枪管受力分析

弹丸挤进过程中，枪管受到弹丸的作用力如图1所示，其中η为缠角，α为导转侧角，β为坡膛角。坡膛部分受力为Fp,阳线受力为Ft，阴线受力为Fs，导转侧受力分别为Fd1、Fd2,则有

F=Fp+Ft+Fs+Fd1+Fd2

(1)

假定其接触面上产生的接触应力分别为σp、τp、σt、τt、σs、τs、σd1、τd1、σd2、τd2，法向应力、切向应力与摩擦因数f呈正比关系，即

(2)

在枪管轴线的力为

Fz=Fpz+Ftz+Fsz+Fd1z+Fd2z

(3)

(4)

研究认为摩擦因数随压力与速度乘积的增大而减小，挤进过程弹丸速度迅速增大，但由于弹丸挤进过程中摩擦力较大阶段历时极短，可忽略其影响，近似认为摩擦因数f不变，黄铜弹丸被甲与枪管之间的动摩擦因数不大于0.05。在此假设条件下，枪管所受弹丸的作用力只与弹丸的挤进位置有关。通过有限元仿真获得的枪管应力与挤进位置数据，从而得到弹丸的挤进阻力。

1.2 挤进时期弹底燃气压力的计算

弹底燃气压力的计算可由形状函数、燃速方程和燃气状态方程联立求解[8]。

简单形状火药的形状函数为

ψ=χZ(1+λZ+μZ2)

(5)

式中：ψ为火药已燃烧的相对质量；Z为火药已燃烧的相对厚度；χ、λ和μ均为火药的形状特征量。

固体火药的燃速方程为

(6)

式中：u1为燃速系数；e1为火药原厚度；c为燃速指数。

由于弹丸挤进时期经历的时间极短，弹丸在枪管内移动的距离不大，可认为此时期为定容燃烧，定容情况下的火药燃气状态方程为

(7)

式中：pB为点火药压力；f为火药力；Δ为装填密度；ρp为火药密度；α为余容。

将该枪械的火药特性参数代入以上各式，联立方程组即可求解出挤进时期的弹底燃气压力曲线。

2 弹丸挤进枪管的有限元模型的建立

2.1 结构模型的建立

以某大口径枪管及3层结构的钢心弹丸为研究对象，枪管无铬层。枪管及弹丸内部结构如图2所示，弹丸由被甲、铅套和钢心3层结构组成。取枪管坡膛起始位置至10倍弹径位置进行分析。

2.2 材料模型

枪管材料为30SiMn2MoVA，仿真中使用应力-应变表定义弹塑性。被甲材料为黄铜，铅套材料为纯铅，由于挤进过程中出现大应变、高应变率、高温和高压等复杂的非线性过程，被甲与铅套材料均采用Johnson-Cook本构模型[9],其本构模型表达式为

(8)

(9)

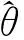
2.3 弹丸挤进过程弹丸载荷的施加

挤进坡膛历时极短，取时间0—0.65ms，将式(1)～(3)联立求得的弹底膛压曲线施加于弹尾横截面，设置枪管外表面为固定约束。接触类型定义为通用接触。

2.4 网格划分

运用HyperMesh划分网格，对枪管阳线部分和弹丸被甲加密划分网格，如图3所示，在仿真过程中采用ALE(ArbitraryLagrangian-Eulerian)自适应网格技术，确保仿真的效率和精度。

ALE自适应网格可以在当材料严重变形时，通过允许网格独立运动，保证高质量的网格，维持网格的拓扑形状。在显式求解器中作为挤进等稳态问题的一种高效求解方法，作为工具来分析稳态问题的瞬态阶段，保证求解的准确性。

3 仿真结果与分析

运用ABAQUS动力显式(Dynamic，Explicit)求解器对上述有限元模型进行仿真和分析。

3.1 仿真结果验证

将仿真得到的弹丸行程曲线与内弹道方程求得的结果进行对比，如图4所示。

仿真得到的弹丸行程与经典内弹道方程计算得到的数据吻合得很好，0.6ms后误差逐渐增大，最大误差不超过10%。证明了弹丸挤进仿真过程的正确性和有效性。

3.2 弹丸挤进阻力分析

由于弹丸有被甲、铅套和钢心3层结构，各层间有弹性塑性形变，以弹丸作为研究对象，较难得到挤进阻力。故将挤进过程中枪管各处应力进行合成得到枪管受弹丸的作用力，进而得到弹丸的挤进阻力随时间的变化规律，如图5所示。为直观研究弹丸的挤进阻力变化规律，从弹丸中部凹槽将弹丸拆分为弹丸前部和后部两部分，由图5可知，弹丸前部和后部分别在0.1、0.4ms与坡膛起始位置接触，挤进阻力迅速增大至峰值后平缓下降，弹丸前部、后部挤进阻力峰值大小基本相同，曲线变化规律大体一致。将弹丸前部和后部挤进阻力叠加后，弹丸整体挤进阻力曲线中出现的短暂下降是由于弹丸中部凹槽不参与挤进过程的缘故。

3.3 弹丸被甲的变形过程

由于弹壳在弹膛中的定位方式采用斜肩定位，弹丸从开始运动到挤进开始有一定距离的自由行程。在0.1ms前，弹丸在火药燃气压力作用下，虽有位移，但并未与坡膛接触。从0.1ms开始，弹丸前部与坡膛起始位置接触，至0.55ms时，弹丸前部通过坡膛结束位置；从0.4ms起，弹丸后部与坡膛起始位置接触，至0.65ms，弹丸后部通过坡膛结束位置，整个挤进过程结束。按照时间顺序，选取弹丸表面刻痕形成的阶段特性图，如图6所示，弹丸逐渐挤进枪管，弹丸表面刻痕由弹丸前部向弹丸后部逐渐延伸，不断加深成形。

3.4 弹丸被甲应力与转速分析

为满足武器的设计要求，弹丸被甲嵌入膛线后在导转侧力的作用下高速旋转，出枪口时获得一定的转速。被甲强度一直是不可忽视的问题。取0.5ms和0.6ms时刻，在被甲表面顺时针依次选取50个结点绕被甲一周，其应力曲线如图7所示。

不同时刻，被甲表面的应力分布基本相同，0.6ms的最大应力比0.5ms增大了5.1%。尽管弹丸为对称结构，但各条刻痕应力分布并不相同，弹丸在挤进过程存在一定摆动。刻痕上应力在364～452MPa范围内，其最大应力为452MPa。非刻痕位置应力在246～357MPa范围内，其最大应力为357MPa。

为了验证弹丸是否获得了足够的转速，将弹丸仿真所得转速与理论转速进行对比，如图8所示。与理论转速曲线平缓地增大不同，仿真转速有一定的波动，这主要是由于弹丸在挤进过程中有一定摆动，一方面摆动会使弹丸转速产生一定波动；另一方面测试点在弹丸质心附近，而弹丸质心并不总在枪管轴线上，测试出来的转速存在一定误差。仿真转速与理论转速在0.3ms前，误差很小；0.3ms后误差逐渐增大，最大误差为12.4%。

3.5 弹丸摆动姿态分析

不考虑挤进过程中枪管产生的振动情况，弹丸初始质心位置位于枪管轴线上，虽然弹丸是对称结构，但挤进过程中弹丸被甲受力不均匀，会产生一定摆动。取弹丸摆动角度为枪管轴线与弹丸质心位移方向之间夹角δ，弹丸摆动情况如图9所示。

图9中所示挤进过程弹丸摆动角共经历了4次较大波动，分别在A、B、C和D处。最大摆动角度在C处为0.022°，该处最小摆动角为0.002 5°，相差约0.019 5°。从挤进开始至0.4 ms，弹丸速度较小，弹丸摆动角度也很小。0.4 ms弹丸前部通过坡膛起始位置，由于弹丸中部凹槽存在，挤进阻力突然变小，导致弹丸受力不均而产生了A处的摆动。0.5 ms弹丸前部开始挤入坡膛结束位置，弹丸产生了B处0.015°大小的摆动角度。C、D处分别是弹丸后部挤入坡膛起始位置和弹丸前部完全通过坡膛结束位置，因而产生很大的摆动角。由此可知，在一定速度下，弹丸通过坡膛起始位置和坡膛结束位置会导致弹丸有较大的摆动，而弹丸中部凹槽的存在，增加了弹丸摆动的次数。

4 结束语

在对某大口径3层结构弹丸挤进枪管过程的建模仿真基础上，验证了仿真结果的正确性，得到了弹丸挤进阻力和被甲表面刻痕的形成过程。仿真的结果表明：挤进过程中，弹丸应力在246～452 MPa范围内，满足强度要求；弹丸能够获得足够的转速；弹丸的摆动姿态与挤进坡膛状态和弹丸外形有一定的关系。该研究可为优化坡膛结构，在满足武器要求的前提下改进弹丸形状以提高弹丸的稳定性提供理论参考依据。

References)

[1]张喜发,卢兴华.火炮烧蚀内弹道学[M].北京:国防工业出版社,2001:47-48. ZHANG Xifa, LU Xinghua. Erosion interior ballistics of gun[M]. Beijing: National Defense Industry Press,2001:

47-48.(in Chinese)

[2]丘尔巴诺夫E B.挤进时期内弹道学与挤进压力计算[M].杨敬荣,译.北京:国防工业出版社1997:13- 20. QIERBAROV E B. Interior ballistics and engraving force calculation during engraving of projectile[M].YANG Jing-rong, translated. Beijing: National Defense Industry Press, 1997:13-20. ( in Chinese)

[3]何勇.弹丸挤进阻力的一维模型与计算[J].弹道学报,1994(4):24-28. HE Yong. The one-dimensional model and calculation of projectile’s engraving resistance[J]. Journal of Ballistics, 1994(4): 24-28. (in Chinese)

[4]何勇.挤进过程实验研究[J].弹道学报,1996(4):37- 40. HE Yong. Research on engraving process experiment[J].Journal of Ballistics,1996(4):37-40. ( in Chinese)

[5]孙河洋,马吉胜,张高明,等. 弹带挤进过程中膛线的应力分析[J].军械工程学院学报,2008,20(4):43- 46. SUN Heyang, MA Jisheng, ZHANG Gaoming, et al. Analysis of the land stress during the engraving process[J].Journal of Ordnance Engineering College,2008,20(4):43- 46. ( in Chinese)

[6]樊黎霞,何湘玥. 弹丸挤进过程的有限元模拟与分析[J].兵工学报,2011,32( 8): 963-969. FAN Lixia, HE Xiangyue. Finite element simulation and process analysis of projectile entering into barrel[J]. Acta Armamentarii, 2011, 32(8): 963 - 969. ( in Chinese)

[7]陆野,周克栋,赫雷,等.某大口径枪械内弹道挤进时期的数值仿真与分析[J].弹道学报,2014,26(2):67- 71. LU Ye, ZHOU Kedong, HE Lei, et al. Numerical simulation and analysis of engraving duration during interior ballistics of some large-caliber small arms[J].Journal of Ballistics, 2014, 26(2):67-71. (in Chinese)

[8]金志明.枪炮内弹道学[M].北京:北京理工大学出版社,2004. JIN Zhiming. Interior ballistics of gun[M]. Beijing: Beijing Institute of Technology Press, 2004.(in Chinese)

[9]JOHNSON G, COOK W. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985,21(1): 31- 48.

Simulation Analysis of Projectile Engraving Process of the Large-caliber Firearm

AN Junbin，LI Qiang，LI Shikang，TAN Qing

(School of Mechatronic Engineering，North University of China，Taiyuan 030051，Shanxi，China)

Aiming at the stress, rotational speed and swing of three-layer structure steel core projectile in the projectile pushing into barrel bore process which is hard to solve through theory and experiment currently, the large-caliber firearm was taken as the research example. The finite element model of projectile and barrel was established by using Johnson-Cook material constitutive relation. The engra-ving process of projectile was simulated by the dynamic explicit method. The pushing resistance of the bullet was researched, and the deformation of the score on bullet shell surface was revealed. The stress and speed of projectiles can be investigated, and the swing angle of projectile can be also analyzed. The result of analysis in this paper can provide some certain references.

barrel; projectile engraving; element method; projectile deformation

10.19323/j.issn.1673-6524.2017.01.004

2016-04-05

基础科研基金资助项目(A0820132003)

安俊斌(1990—)，男，硕士研究生，主要从事射速发射理论与技术研究。E-mail：1@huadey.com

TJ012.1

A

1673-6524(2017)01-0017-05