复杂网络相继故障的节点动态分析
徐 野,王 瑶
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159)
复杂网络相继故障的节点动态分析
徐野,王瑶
(沈阳理工大学 信息科学与工程学院,辽宁 沈阳 110159)
摘要:针对复杂网络相继故障问题,选取小世界和无标度两种经典的网络进行网络鲁棒性分析。首先对网络节点进行随机性和确定性两种策略的攻击,基于崩溃节点负荷局域择优重新分配原则,建立两种网络的相继故障模型并分析节点的动态鲁棒性。数值模拟得出与理论相一致的结果。然后进一步研究了网络负载以及网络冗余对网络鲁棒性的影响,用毁坏网络节点的数目与最大连通子图相对值G之间的关系体现网络鲁棒性能。结果表明,网络冗余越大以及网络负载越小均能使网络的鲁棒性能增强。实验的数值模拟结果均与理论分析一致。
关键词:复杂网络;相继故障;鲁棒性;攻击;网络负载
真实世界中大量功能各异的系统都可以通过网络加以描述。例如,人类社会是人通过各种社会关系连成的网络,因特网是由路由器和计算机通过通信介质连成的网络,类似的还有电力网络、交通网络等[1-2]。这些网络具有很高的复杂性,因此被称为“复杂网络”。由于复杂网络理论的不断完善和发展[3-5],很多研究者开始将这一理论方法结合系统科学和复杂性科学,对网络的相继故障及其鲁棒性进行理论解析、数值分析等,取得了令人瞩目的成果。
由于网络的开放性,不同团体、不同国家都可以互连,更由于计算机攻击者的存在,使得网络的安全问题凸显出来。如今随机故障和蓄意攻击鲁棒性问题[6-8],已经成为研究的热点。在这一方面,Albert(2000)等[5]较早地针对这一问题进行了研究,得出无标度网络的一个基本特性是对随机故障的鲁棒性和对蓄意攻击的脆弱性,并且指出产生这种现象的原因在于无标度网络中度分布的不均匀性。随后许多学者都对网络的鲁棒性做了进一步的研究。但是Albert以及后来的大部分研究者都仅仅只是从静态的角度研究网络鲁棒性,即节点的故障或者移除仅仅存在于网络拓扑意义上,对其它节点的存在与否没有任何影响,并没有考虑到网络的动态特性。而在很多实际网络中,一个或者几个节点或边发生故障(这种故障可能是随机发生的,也可能是蓄意攻击造成的)会产生负荷重分配问题,即会通过节点之间的耦合关系引起其他节点发生故障,这样就会产生一种连锁效应,最终可能导致相当一部分节点甚至整个网络的崩溃。这种现象称为相继故障,有时也称为“雪崩(avalanche)”。例如,在Internet[9-12]中,对少数路由器进行病毒攻击会导致路由器过载,迫使数据包重新路由,引起其它路由器接连过载,产生雪崩效应。大规模的相继故障一旦发生,往往具有极强的影响力和破坏力。例如,2003 年8月由美国俄亥俄州克利夫兰市的 3 条超高压输电线路相继过载烧断引起的北美大停电事故使得数千万人陷入黑暗,经济损失估计高达数百亿美元。在社会与经济网络中也会发生类似的雪崩效应,二十世纪九十年爆发的亚洲金融危机就是一个典型的例子。因此,有必要对相继故障的发生机理、相继故障的预防与控制做深入的研究。
1 模型算法与理论分析
1.1 网络拓扑结构
复杂网络有等级网络、无标度网络、小世界网络、随机图、规则网络等多种类型,为了更好地研究其鲁棒性,考虑选择一些典型的拓扑网络来更好地理解与控制因相继故障导致的一系列问题。采用NW小世界网络和无标度BA网络两种典型的复杂网络。
1.1.1 小世界网络
小世界网络是完全规则网络向完全随机图的过渡的一种网络,它具有两个显著的统计特征,其一是具有较高的聚集系数,与规则网络类似:其二是具有小的平均路径长度,与随机网络类似。这种特殊结构的网络被称为小世界网络[8]。在理论分析上,NW小世界模型要比WS小世界模型简单一些,所以文中采用NW小世界模型进行理论研究。具体构造算法[8]如下:
1) 从规则图开始:考虑一个含有N个点的最近邻耦合网络,它们围城一个环,其中每个节点都与它们左右相邻的各K/2节点相连,K是偶数。
2) 随机化加边:在随机选取的一对节点之间以概率P加上一条边。其中,任意两个不同的节点之间至多只能有一条边,并且每一个节点都不能有边与自身相连。
在NW小世界模型中,P=1对应于全局耦合网络,P=0对应于原来的最近邻耦合网络。当P足够小和N足够大时,NW小世界模型本质上等同于WS小世界模型。
1.1.2 BA无标度网络
为解释幂律分布的产生机理,1999年Barabási 和Albert[1]提出了一个无标度网络模型,现在被称为BA模型。无标度网络的连接过程遵照偏好依附的原则进行,当网络中新节点出现时,更倾向于连接到已经有较多连接的节点,随着时间的推进,这些节点拥有比其他节点更多的连接数目,这种“富者欲富”的现象也称为“马太效应”。BA网络模型构造算法[9]如下:
1) 初始状态:m0个初始节点,且各节点之间均相连。
2) 增长:每增加一个节点,增加的连接数为m,这里m≤m0。
3) 优先连接:一个新节点与一个已经存在的节点i相连接的概率Π与节点i的度ki节点j的度kj之间满足如下关系:
(1)
经过t步时间步后,BA模型演化成一个具有N=t+m0个结点mt条边的网络。
1.2 网络负荷的理论分析
相继故障是一种类似于网络上的传播行为的一种现象。本文主要研究一个节点的移除或者故障所导致网络的全局动态属性,即网络的动态相继故障分析。初始阶段,给予每个节点上的负荷都小于它的安全阈值(处理能力),网络处于稳定状态。此时对其中的一个节点i进行某种攻击,令其发生故障,于是失效节点上的负荷会依据负荷重分配原理重新分配到邻居节点上。负荷的重新分配可能会引发其他节点产生故障,当网络中剩余的节点负荷都低于其安全阈值时,相继故障结束,此时网络重新达到稳定状态。这种某几个节点的崩溃产生连锁反应,最终导致相当一部分节点甚至整个网络的崩溃。如Internet的拥挤和电力网络的停电事故等。因此探讨不同类型的节点在相继故障中的作用显得非常重要。
根据现实网络中,节点的负荷与节点本身的度具有一定的关系:
1) 网络中度越大的节点,其负荷程度越高,假设网络中每一个节点j的初始负荷Lj和它的度存在以下数学关系:
Lj=b×Kα+β
(2)
式中:b、α、β均为可调参数,b是倍乘系数,缺省为1;α是指数系数,它帮助实现度越大时,节点负载能力越强,有研究表明,α为1时,系统性能最强;β是衰减函数,它表示节点负载能力与节点度成不完全正比关系,一般是一个衰减方程β=1/(1+exp(-g×K/sum(K)))。以往许多研究中都采用类似的负荷方式,并且符合现实的网络,所以假设合理。
2) 崩溃节点i上的负荷重新分配到它的邻居节点j上,依据择优概率:
(3)
式中:Γ表示为节点i的所有邻居节点的集合。
3) 于是可以得出,当节点i崩溃后,它的一个邻居节点j收到的额外负荷ΔLji为
(4)
考虑到现实因素,节点处理负荷的能力要受成本的约束。将节点的负荷定义为该节点的介数(betweennesscentrality,BC),它反映了网络中通过该节点的最短路径的数目。定义节点j的容量(可承载的最大负荷)正比于其初始负荷Lj,即
Cj=(1+α)Lj,j=1,2,…,N
(5)
式中常数α≥0是一个容许系数。正常情况下,网络运行于一种自由流的状态。当网络中某个节点发生故障时,或者它所收到的负荷加上本身节点上的初始负荷大于它的处理能力,即Cj 当网络相继故障过程结束后,采用最大连通子图相对值G来衡量网络的崩溃程度。G定义为最大连通子图的规模N′与原始网络规模N的比值,即 G=N′/N (6) 式中N′表示相继故障结束后网络的最大连通子图包含的节点个数,N表示原始网络节点数。 实验基于Matlab平台实现网络模型的构造以及数值仿真。 按照上述算法分别构造一个NW小世界网络(图1)和BA无标度网络(图2)。为了便于清楚地观察网络的特性以及对节点摧毁的鲁棒性,选择50个节点进行实验。 图1 NW小世界网络 图2 BA无标度网络 参数设定:小世界网络N=50,m=4。N为络节点数;m为每个节点连边的最近邻节点数。无标度网络N=50,m=3,m0=3。m为每增加一个节点,增加的连接数;m0为初始节点数。 为了更好对比两种网络的鲁棒性,采用对节点进行随机性攻击与确定性攻击的两种策略进行仿真分析,选50个节点作为模拟研究对象。 实验参数设定:τ为攻击标度,取值区间为[0 1],τ=1表示完全随机性攻击,τ=0时称为完全确定性攻击,即蓄意攻击网络中度最大的节点;ω为网络负载,取值为[0 1],ω=1表示网络满负荷,ω=0表示网络零负荷;θ为网络冗余,取值为[0 1],其值越大表示网络的冗余程度越高,但同时网络构建与维护成本增加。 1) 取ω=0.5,θ=0。分别取τ=0,τ=1初步观察两种网络对确定性攻击和随机性攻击表现出的鲁棒性(图3)。图3中曲线1、2和曲线3、4分别代表小世界网络的变化和BA无标度网络的变化。 分析图3易知,在同等条件下,NW小世界网络对两种攻击的鲁棒性差异较小,BA无标度网络对随机性攻击有较好的鲁棒性,而在确定性攻击中表现了极端的脆弱性;τ=0时,小世界网络曲线下降速度慢,且明显在BA无标度网络曲线的右边。所以可知NW小世界网络对确定性攻击的鲁棒性比BA无标度网络强。而在随机性攻击中,BA无标度网路又显示出比NW小世界网络更好的鲁棒性。以上结论也证明了以下结论:BA无标度网络的节点符合幂律分布,其节点度的分布不均匀性导致网络对蓄意攻击的极端脆弱性和对随机攻击的高度鲁棒性。小世界网络的节点度分布近似均匀,对蓄意攻击和随机攻击没有表现出如BA网络的极端特性。 图3 两种网络分别在两种不同攻击策略下的对比图 2) 分别取τ=0,τ=1;θ=0,即研究网络无冗余的状态下,对两种网络进行随机性攻击和确定性攻击,图4为两种网络在不同的节点负荷下,观察网络的崩溃程度G与网络负载的关系。 分析图4可知:1)网络负载越大,曲线下降的越快。可知网络越大,两种网络均崩溃的越快。进一步观察BA无标度网络的曲线,ω=0时,当随机攻击毁伤网络节点总数的20%,网络的崩溃程度才不到20%,而在确定性攻击中,毁伤网络20%的节点,网络的崩溃程度已达50%;ω=0.5时,随机毁伤节点数达到35%,网络开始完全崩溃,确定性毁伤10%左右的节点,网络已经完全崩溃;ω=1时,只需随机毁伤网络节点总数的0.1%,即可使网络完全崩溃,此时确定性毁伤节点不到0.02%,即可使网络完全崩溃。同理可分析小世界网络。由此可得出网络的负载较高时,网络基本上处于崩溃边缘,稍微增加毁伤节点,网络就能从鲁棒状态迅速转向崩溃状态。2)对比两图,依然可以发现,两种网络均在随机性攻击下表现出较好的鲁棒性,而BA无标度网络也依然对随机性攻击表现出极端的脆弱,说明网络的负载不影响网络本身的特性,只是在网络的相继故障中起着催化的作用。 图4 两种攻击下网络崩溃速度与网络负载的关系 3)分别取τ=0,τ=1;ω=0.5,即研究网络在相同负载下,对两种网络进行随机性攻击和确定性攻击,图5为两种网络在不同的网络冗余下,网络的崩溃程度G与被摧毁节点数目的关系。 图5 两种攻击下网络崩溃速度与网络冗余的关系 分析图5可知,无论是随机性攻击还是确定性攻击,在固定网络负载的情况下,对于两种网络来说,网络冗余θ的增大都导致网络性能的各项指标临界点的右移,相继故障的产生受到限制,网络的鲁棒性得到极大改善。但是虽然增加网络冗余度可以增强网络的性能,至极端情况,当网络转化为全连通网络时,网络的鲁棒性能达到最佳值,但此时网络构建的成本与维护成本相对增加。网络负载的加大也能使网络的冗余度增加,但当网络负载过重时,网络的鲁棒性能也会大幅度降低。 (1) 研究了复杂网络中BA无标度网络与NW小世界网络的相继故障模型及其鲁棒性,通过随机攻击和蓄意攻击,讨论了两种网络的鲁棒性以及其与网络负载和网络冗余的关系。通过对比分析,鲜明地突出两种网络的特性。涉及到现实网络的研究,而实际网络数据和模型模拟的结果有很大区别,因此对现实网络相继故障及其鲁棒性研究更有意义。 (2) 对于网络的动态鲁棒性问题,当前只能采用简单的数值模拟进行分析,解析计算比较困难,有待于进一步研究与探讨。本次实验取两种网络中各50个节点做研究,样本容量相对较小,实验结果存在一定误差。 (3) 本次实验只针对网络节点做了研究,未对网络边做处理。如何分配网络的权重以提高网络抵抗故障的能力。一方面,缺乏给网络中边定义权重的一般方法;另一方面考虑权重后,权重又是怎么影响网络的性质、结构和效率等问题也没有合理科学的定义。因此,对这些问题进行更深一步的探讨具有重要的意义。 参考文献: [1]GUDIVADAVN.InformationRetrievalontheWorldWideWeb[J].IEEEInternetComputing,1997,1 (5):58-68. [2]WatsDJ,StrogatzSH.CollectiveDynamicsofSmall-worldNetworks[J].Nature,1998,(393):440-442. [3]STROGATngSH.ComplexNetworks[J].Nature,2001,(410):268-276. [4]MilgramS.Thesmall-worldproblem[J].PsycholToday,1967,(2):60-67. [5]AlbertR,JeongH,BarabsiAL.Attackanderrortoleranceincomplexnetworks[J].Natrue,2000,(406):387-482. [6]GOHKI,KAHNGB,KIMD.Fluctuation-DrivenDynamicsoftheInternetTopology[J].Phys.Rev.Lett,2002,(88):98-101. [7]WATTSDJ,STROGATZSH.Collectivedynamicsof‘small-world’networks[J].Nature,1998,393(6684):440-442. [8]汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006. [9]徐野.基于大范围模式的互联网拓扑建模[M].北京:电子工业出版社,2011. [10]任俊亮,申卯兴.无尺度网络中降低相继故障规模的策略研究[J].计算机工程与应用,2011,47(33):82-161. [11]丁琳,张嗣瀛.复杂网络上相继故障研究综述[J].计算机科学,2012,8(39):8-25. [12]王建伟,荣莉莉.面向相继故障的复杂网络上的边袭击策略研究[J].中国管理科学,2009,1(17):126-130. (责任编辑:马金发) Research of Dynamic Failure Nodes in Cascading Failure Complex Networks XU Ye,WANG Yao (Shenyang Ligong University,Shenyang 110159,China) Abstract:In view of the complex network cascading problem,small world and scale-free network of the classical network is selected to analyze the robustness.Firstly,in order to attack the network with the randomness and definiteness,two kinds of network cascading failure model and analysis of dynamic node robustness are set up,which is based on collapse node load local preferential redistribution principle.Then further research is on network load,and network redundancy affects the network robustness.With the destruction of network nodes and the opposed value G to a maximal connected subgraph to express the network robustness,it is shown that the larger the network redundancy is,the smaller the network load is,which makes the network robust performance enhance.Simulation results are consistent with the theoretical analysis. Key words:complex networks;cascading failure;robustness;attacks;network load 中图分类号:TP393 文献标志码:A 文章编号:1003-1251(2015)01-0017-05 作者简介:徐野(1976—),男,副教授,博士,研究方向:复杂互联系统与大规模网络. 基金项目:国家自然科学 资助(61373159);沈阳市科技应用基础研究计划项目资助(F13-316-1-22) 收稿日期:2014-04-301.3 分析网络相继故障结果
2 数值分析
2.1 仿真软件
2.2 构造网络模型
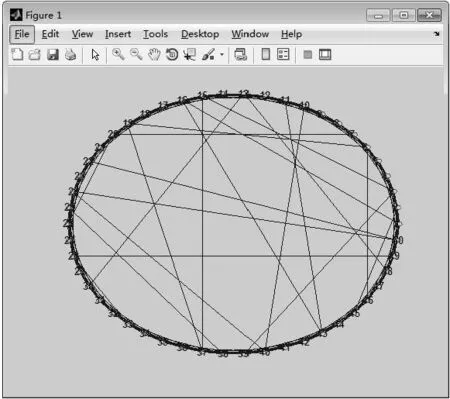

2.3 节点故障分析



3 结束语

