高校学生缺课模型分析及点名策略
李 硕 管白楠 马园媛 魏成花
(1.昌吉学院数学系 新疆 昌吉 831100;2.昌吉学院机关 新疆 昌吉 831100)
引 言
随着教育资源的广泛推广,我国的高等教育由以前的精英教育模式已经转化到了大众化教育模式,而有限的教育资源制约着受教育者的数量.目前就业压力的竞争加大,热门专业的学员更热,人数更为庞大,面对接踵而来的广大学员,高校一般实行合班大课堂来应对广大学员公平受教育.然而,大班上课人数多,管理较难,易于发生逃课现象[1].高校学生逃课现象的普遍存在,无不与学生个性的不同、学校教学管理的不足、社会各种环境的差异、学生的自身等多种因素存在关系[2].当前,考证热、考研热等是大学生盲目逃课的一大原因.大学管理制度的不完善、教师授课水平的差异成为大学生逃课的第二原因。大学生的家庭条件、学习兴趣、上网瘾、打牌瘾等是其逃课的第三原因[3].
针对学生逃课频发现象,实施有效的点名策略是教师考察学生出勤的一个关键问题.课堂点名方式繁多,最常用的点名方式就是点名喊到,点名过程不仅仅是教师检查学生上课的出勤情况,还蕴含着许多有意义的教育价值,如果教师采取灵活多变的随机抽样点名方式,不但能有效地减少点名所花费的时间,而且还能有效地估算大合班学生出勤情况,这为我们研究高校学生点名策略提供了必要的现实意义.我们应用数理统计知识,从大样本(大合班学生总数)中抽取小样本(被点名的学生人数)的方法来研究学生上大班课的点名策略,从而估计学生整体的出勤情况.样本含量体现研究设计中重复原则,其意义在于估计研究中的误差,且抽样误差大小与样本量有关,足够的样本量也是实验研究中保证组间均衡性的基础[4].我们假设的样本含量是参与上课的大班学生(约100人左右),逐人点名方法意味着教师要付出更多的时间、精力、人力,造成不必要的浪费,逐人点名还会降低课堂授课的时间效率.如果在大班中点名的样本例数太少,就易于把偶然性或巧合的现象当做必然的规律现象,也不能正确的估计学生的出勤率,导致了结论的可靠性差、用于推断总体的精度差、检验效能低,最终总体中存在的差异未能检验出来,出现假阴性结果(隐藏),即对大合班学生实施点名策略既不能片面追求增大样本的逐一点名方法,也不能忽视保证足够的样本含量来估计学生的出勤率.
对于大合班上课学生易逃课频发现象,我们通过简单随机抽样方法,能够有效的估算出该大班学生出勤情况,同时构造出了小样本估算出勤率的95%的置信区间,数值模拟显示该班出勤率在小样本估算出勤率的95%的置信区间内.
1 缺课模型分析
对总体率π做估计调查的样本大小模型[5]为

其中:zα2表示正态分布的α2分位数,δ为容许的误差(允许样本率p和总体率π的最大容许误差)。
下面我们应用上述模型研究高校学生大合班上课随机抽样需要被抽点的人数,为估算学生出勤率提供有效方法。
案例:某高校教师对某专业大班上课的出勤率进行调查,在预调查中这个比例是90%,希望所得的样本率p和总体率 π之差不超过10%的可能性不大于0.05,需要被点多少名学生可以有效的估算出该班的出勤率.
案例分析:应用数理统计知识,采用统计学检验时,当研究结果高于和低于效应指标的界限均有意义时,应该选择双侧检验,所需样本量就大;进行双侧检验时,α的zα2界值通过查标准正态分布表得到.α水平由研究者具体决定,通常α取0.05.于是
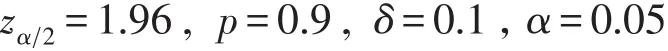
利用公式(1)得

以某高校大合班全体学生作为研究对象(假设100人),除去请假(事假、病假)外,选择90人作为我们的研究对象,现在研究90人中学生的上课情况,上课情况分为两类:一类上课;另一类逃课.这90人的上课情况构成了一个样本空间S={X1,X2,…,X90},其中{Xi=0}表示某学生逃课,{Xi=1}表示某学生上课,i=1,2,…,90.于是我们研究的问题是该选择多少研究对象才能有效估计该班学生的出勤率.
2 数值模拟及结果分析
假设某大合班需要研究对象90人,逃课人数是8人,则该大合班的出勤率为(90-8)/90=0.9111,利用公式(1)计算出需要被调查的人数n=35人,采用简单随机抽样从样本空间中抽取35人,用这35人(小样本)可以估算出大班学生的出勤率.
根据假设,大班有90人,逃课8人,则该样本空间S就由8个0和82个1组成,利用Matlab软件进行数值模拟:在S中随机抽取n=35,然后利用软件统计出35个数中1的个数(相当于统计抽取的35个学生中上课人数),计算出样本出勤率,同时构造出样本出勤率的95%的置信区间.
其中:cql表示全班学生出勤率;cql1表示小样本出勤率;x表示样本均值;s表示样本方差;α=0.05,tα2(n-1)表示自由度为n-1的t分布的α2分位数,n是小样本个数,于是就有:
小样本学生的出勤率与全班学生出勤率的误差δ1=|cql-cql1|,小样本出勤率的95%的置信区间记为[LC,RC],
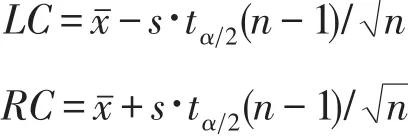
模拟结果:
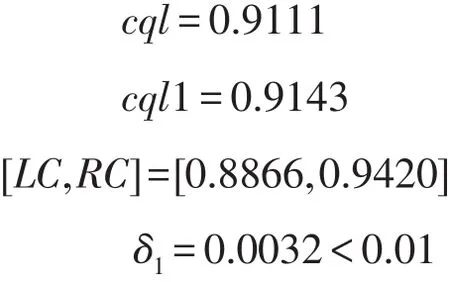
模拟结果显示:全班学生出勤率(cql)在95%的样本出勤率的置信区间[LC,RC]内。样本出勤率与总体出勤率的误差δ1=0.0032,远远不超过0.01,这一结果在原题设容许的最大误差范围内,模拟效果显著.从而说明在大合班进行课堂授课的教师只需随机抽取其中的35名学生作为点名对象,就可以有效的估算出全班学生的出勤情况,从而为高校教师在学生考勤方面提供了定量化的策略.当然,实际教学中教师们还有一些非定量化策略,详细情况参见[6-9].
[1]程芳玲,杨百勤.大学生逃课现象的分析及思考[J].中国轻工教育,2004,(4):41-42.
[2]张婵香.大学生逃课的福利损失分析及对策[J].现代教育科学,2013,(4):42-45.
[3]徐松芝,刘嘉诚,袁朝庆.浅谈大学生逃课原因及其对策[J].长春理工大学学报,2012,7(1):107-108.
[4]茆诗松.概率论与数理统计教程(第二版)[M].北京:高等教育出版社,2011.
[5]蒋兴国.临床医学研究对象样本量的估计[J].宁夏医学杂志,2008,30(6):571-573.
[6]赵洋.席位分配及课堂点名模型的研究[M].陕西:西北工业大学,2006.
[7]郭冬生.我国大学本科教育管理制度的反思与重建[J].清华大学教育研究.2004,(6):64-70.
[8]晏成宗.扩招背景下学生缺课现象的经济学分析[J].高教论坛,2006,(3):42-44.
[9]李小春,蔡湘文.课堂点名的数学模型[J].铜仁学院学报,2013,15(2):125-127.

