解析几何例题教学的4个层次——从一道联赛试题到高考试题

●施哲明(嵊州市教研室浙江嵊州312400)

解析几何例题教学的4个层次
——从一道联赛试题到高考试题

●施哲明(嵊州市教研室浙江嵊州312400)

解析几何在高中数学学习过程中的重要性是不言而喻的，而对解析几何例题教学的重视更不容忽视.很多学生能听懂老师的讲解，而一旦自己解题，则往往得不到最后结果.在此过程中，教师的原因值得我们关注.数学内容、知识、方法往往要通过具体的例题教学来呈现，但是教师在呈现的过程中，有时不得法，从而导致学生看得懂但做不了.本文通过一个例题，呈现解析几何例题教学的4个层次，期望能有助于教师对解析几何例题教学更本质的认识.

例1在平面直角坐标系xOy中，P是不在轴上的一个动点，满足条件:过点P可作抛物线y2= 4x的2条切线，2个切点连线lP与PO垂直.设直线lP与直线PO，x轴的交点分别为Q，R.

1)证明:R是一个定点;

(2014年全国高中数学联赛试题)

1 第一层次:摸清题情，挖掘背景

首先阅读题目，找到关键词，然后搜索这个关键词在头脑中已有的知识.在本题中，最显眼的是“切线”，然后是“垂直”.而对于垂直而言，学生基本上能明确垂直与斜率之间的关系.因此，对本题来说，需要寻求更多的是与“切线”有关的背景.

问题1如何求经过抛物线上一点的切线方程?

例2求经过抛物线y2=2px(其中p＞0)上一点P(x0，y0)的切线方程.

解设切线方程的斜率为k，则切线方程为

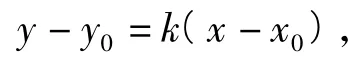
联立y2=2px，得

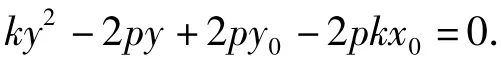
由相切可知Δ=0，即

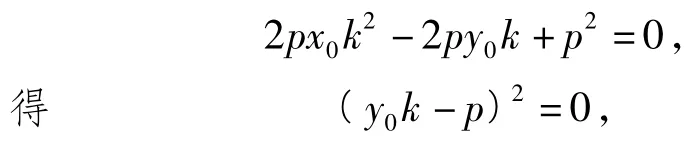
于是切线方程为y0y=p(x+x0).

尽管这是一个抛物线切线方程的基本结论，但在教学中我们要遵循“知其所以然”的原则，让学生有一个体会实践和深刻理解的过程，而不仅仅是一个结论的直接应用，这在教学过程中是值得我们关注的.当学生得到了这个结论之后，教师可以从求解方法上、结论形式上给予指导，加深学生的记忆和理解.

问题2过抛物线外一点作切线，如何求切线的方程呢?

例3过抛物线y2=2px(其中p＞0)外一点P(x0，y0)作切线，求切线方程.

分析一般地，我们不考虑特殊情况，即x0≠0，y0≠0，设切线的斜率为k，则切线方程为

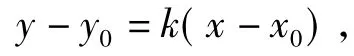
联立y2=2px，得

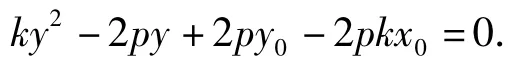
由相切可知Δ=0，得

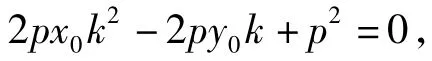
此为关于斜率k的一元二次方程，一般情况下，可以求得2个k的值，从而得到2条切线方程.

2 第二层次:顺藤摸瓜，“边走边看”

当头脑中已有关于切线的一些信息后，再回头看题目，并根据题意要求，顺藤摸瓜.“过点P可作抛物线y2=4x的2条切线，2个切点连线为lP”，显然，目标为直线lP的求解.

问题3过抛物线外一点作抛物线的2条切线，如何求2个切点所在的直线方程呢?

例4过抛物线y2=2px(其中p＞0)外一点P(x0，y0)(其中P(x0，y0)不在坐标轴上)作切线，切点分别为A，B，求切点所在弦AB的直线方程.

分析显然切点所在弦AB的直线方程必与切点有关，若设切点分别为A(x1，y1)，B(x2，y2)，则由例2可得相应的切线方程，但切线是从点P(x0，y0)出发的，因此点P(x0，y0)的坐标满足切线方程.这样“边走边看”，得到的又将会是怎样的式子呢.

例1的解1)设切点分别为A(x1，y1)，B(x2，y2)，则由例2的结论可得过点A，B的切线方程分别为

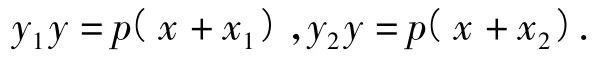
因为切线都经过点P(x0，y0)，所以

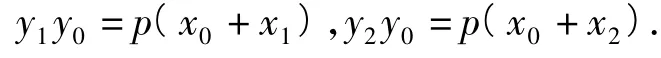
又因为经过点A(x1，y1)，B(x2，y2)的直线方程是唯一的，所以直线AB的方程为

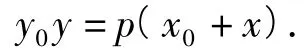
接着就是顺水而下，由“lp与PO垂直”可得

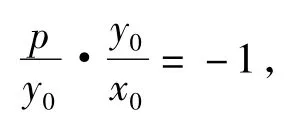
即x0=－2.此时直线lp的方程为

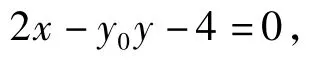
直线lP与x轴的交点R为定点(2，0).

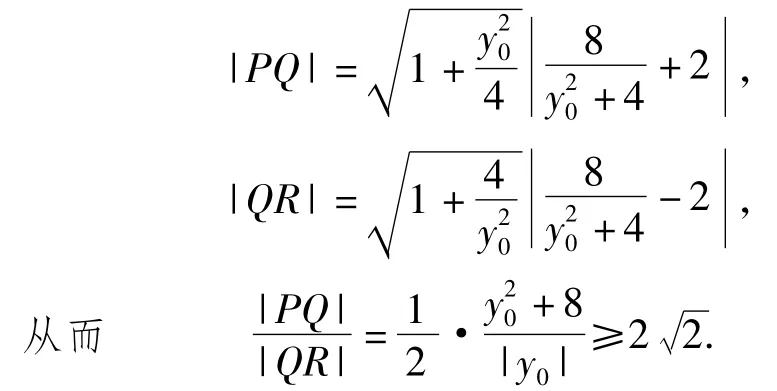
在很大一个层面上看解析几何题的求解，基本上可以根据题意的要求“顺水而下”，或者用通俗的语言来表达，虽然有时会出现文字语言与数学语言的相互转换，但这往往不是关键之点.

3 第三层次:总结方法，拓展结论

从方法的角度来看，一方面体现解析几何的常规解法，欲求什么就设什么，如例2、例3，欲求切线方程，先设斜率k，再求出k的值.另一方面，设而不求的方法运用，恰好体现出解析几何中最重要的数学思想，如例4，设出切点A(x1，y1)，B(x2，y2)，但并没有真正去求x1，y1，x2，y2.

从结论的角度来看，可以得到:

结论1抛物线y2=2px(其中p＞0)上一点P(x0，y0)的切线方程为y0y=2p(x+x0).

仔细观察一次项和二次项的系数，可以先把y2看成y·y，把x看成，然后把其中的一个y记为y0，把其中的一个x记为x0，这样就得到y0y= p(x+x0).当然，这样的一种方式无非便于学生的理解和记忆而已，但确实对于一般的二次曲线都有这样的结论.

结论2过抛物线y2=2px(其中p＞0)外一点P(x0，y0)(其中P(x0，y0)不在坐标轴上)作切线，切点分别为A，B，则切点所在弦AB的直线方程为y0y=p(x+x0).

同样，对于圆、椭圆、双曲线都有类似的结论:

从特殊的抛物线得到的结论，拓展到一般的抛物线所具有的结论，再从抛物线的结论拓展到更一般的圆锥曲线所具有的特征，这样既从曲线类型上进行拓展，又从方式上进行发散，不仅有助于学生更系统地掌握圆锥曲线中与切线有关的知识，也有助于为学生提供解析几何问题的思考方向.数学教学永远离不开例题，但是就题论题的例题教学效果微乎其微，充其量也只不过是能解此题而已，如何从所选的例题中尽量多地反映出数学的知识性和方法性呢?显然，方法的总结、结论的拓展是必不可少的，也是至关重要的一个环节.

4 第四层次:延伸应用，相得益彰

为进一步加深对所学知识的印象以及方法的应用，练习的环节也是必不可少的.不仅如此，通过练习，还可以提高学生的解题速度和数学思维能力.当然，对于练习题需要作精心选择，既要能紧紧围绕所学的知识和方法，又要具有时代性和新颖性.

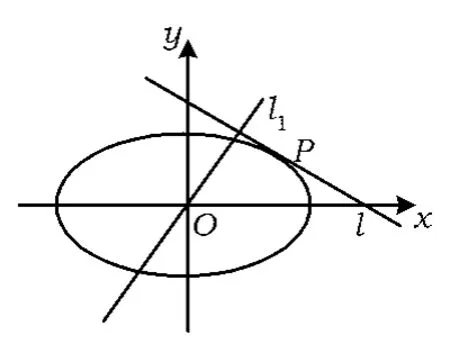
图1

1)已知直线l的斜率为k，用a，b，k表示点P的坐标;

2)若过原点O的直线l1与l垂直，证明:点P到直线l1距离的最大值为a－b.

(2014年浙江省数学高考理科试题第21题)

解1)设P(x0，y0)，则由结论3可知，直线l的方程为，故直线l的斜率为

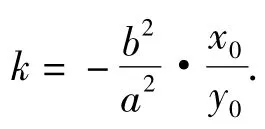
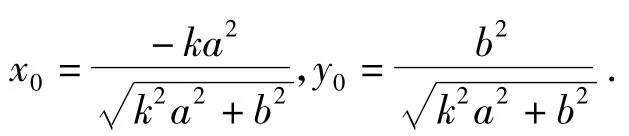
2)因为直线l1与l垂直，而由第1)小题可知直线l的斜率为，又直线l1经过原点，所以直线l1的方程为

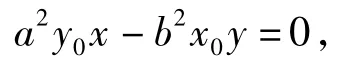
故P(x0，y0)到直线l1的距离为

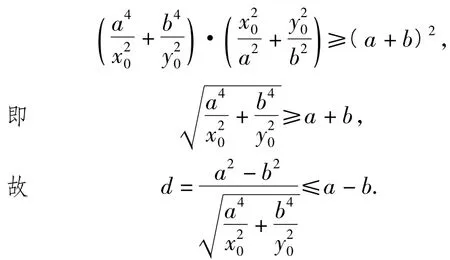
选择最接地气的2014年数学高考题，既体现了时代性，又体现新颖性，特别是与命题组提供的解法不同的求解过程，确实能让学生感受到学习数学知识和数学方法的必要性，从而激起他们学习数学的积极性，真可谓是相得益彰!