数学综合题求解中的“优先思维”策略

●张金良(浙江省教育厅教研室浙江杭州310012)

数学综合题求解中的“优先思维”策略

●张金良(浙江省教育厅教研室浙江杭州310012)

众所周知，数学综合题是最具区分度的一类试题，通常有多种解法.但在求解过程中快速选择较为简洁的解法并非易事，它需要解题者具备良好的知识结构、丰富的解题经验和洞察题目本质的能力.根据笔者近年来的解题实践发现，在解题的初始阶段，哪些已知条件必须优先使用，哪些解题方法应该优先考虑，对解题者来说十分重要，它不仅保证了解题者思维起点的合理性，也优化了解题的过程.下面例析数学综合题求解时6种常用的优先思维策略，供研讨.

1 使用定义优先

数学定义是数学概念学习的核心内容，是其他相关知识的基石，解题时若能重视定义的使用，甚至优先考虑定义的使用，可轻车熟路，快速求解.

例1F1，F2为椭圆的2个焦点，过F2的直线交椭圆于点P，Q，PF1⊥PQ且|PF1|=|PQ|，求椭圆的离心率.

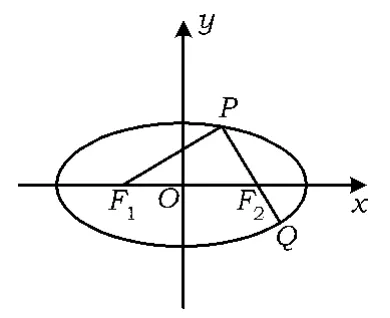
图1

分析这是一道常见的直线与圆锥曲线的相关问题.若选择焦点弦长及距离相等来解题，则会陷入繁难的演算.若能优先使用圆锥曲线定义就十分简便.下面给出略解.

解联结F1Q，由题设|PF1|=|PQ|=m，得，由椭圆定义知

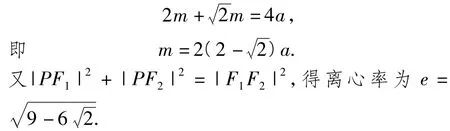
例2设数列{xn}满足x1=1，，［x］为不超过实数x的最大整数，证明:对任意正整数n，有2n|xn+2.

分析本题乍看，无从入手，但注意到［x］的定义，将其呈现出来并作适当的变形，问题就一目了然，简证如下.

证明根据［x］的定义，知

下面用第二数学归纳法，容易证明(略).

2 分析几何背景优先

对于一些复杂的代数综合题，若优先考虑其几何特征，即便是大致的图形，也可利用几何直观性迅速找到解题的突破口.

例3已知a是给定的实常数，设函数f(x)=(x－a)2(x+b)ex，b∈R，x=a是f(x)的一个极大值点.

1)求b的取值范围.

2)设x1，x2，x3是f(x)的3个极值点，问是否存在实数b，可找到x4∈R，使得x1，x2，x3，x4的某种排列xi1，xi2，xi3，xi4(其中i1，i2，i3，i4={1，2，3，4})依次成等差数列?若存在，求所有的b及相应的x4;若不存在，说明理由.

分析这是2010年浙江省数学高考理科压轴题.试题新颖别致，令无数考生又痛又喜，全省得分率为0.25.绝大多数学生畏惧于形式化的数学表示和开放性的设问，但若能将函数的草图大致画出来，就能迅速求解.下面给出略解.

解很明显，a是函数的二重零点，当x趋向于正无穷大时，f(x)趋向于正无穷大，当x趋向于负无穷大时，f(x)趋向于0，于是结合题目画出草图如图2所示:

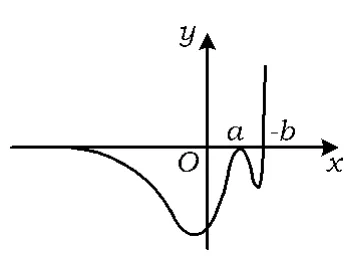
图2

观察图形知a＜－b，又f'(x)=(x－a)［x2－(a－b－3)x－a－ab+2b］ex.记h(x)=x2+(－a+b+3)x－ab－a+2b的2个零点分别为x1，x3，且x1＜a＜x3.

当x1+x3=2a，即a－b－3=2a时，易知Δ=(a+b－1)2+8=26，，于是由等距几何意义得

当x1+x3≠2a时，结合图形与等差数列性质知，x4，a是x1，x3的三等分点，则

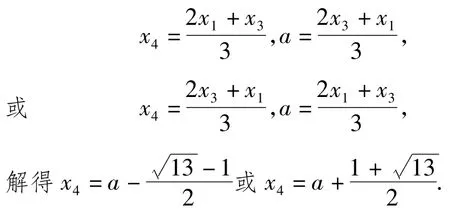
点评运用数形结合解题是十分重要的思想方法之一，但学生限于知识深广度的制约，对诸如

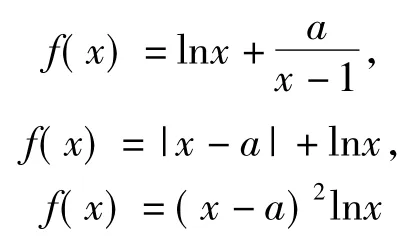
等函数模型就难以勾勒其草图，影响解题.

3 观察特殊情形优先

有些含参数的综合题，往往需要分类讨论来求解，但若不缩小参数的讨论范围，机械地逐类讨论，则会陷入繁难的境地，甚至无法完成解题任务.有时若优先考虑特殊情形，则可缩小参数的讨论范围，大大降低了解题难度.

例4已知函数f(x)=x3+λx2+(2λ－3)x(其中λ∈R).设函数f(x)除0外还有2个不同的零点x1，x2(其中x1x2≠0，且x1＜x2).若对任意的x∈［x1，x2］f(x)＞f(－4)恒成立，求实数λ的取值范围.

分析从题型上看，本题属于函数恒成立问题.测试表明大多数解题者先求导找出极值点，然后分类讨论，设法求出函数在［x1，x2］上的最小值，再令该最小值大于f(－4).虽想法可行，但真正实施时却难似上青天.若细细琢磨，发现若优先考虑特殊情形、内隐条件和几何意义，此题便可迎刃而解.下面给出略解.

解由题意f(x1)＞f(－4)，得

又函数f(x)除0外还有2个不同的零点，从而

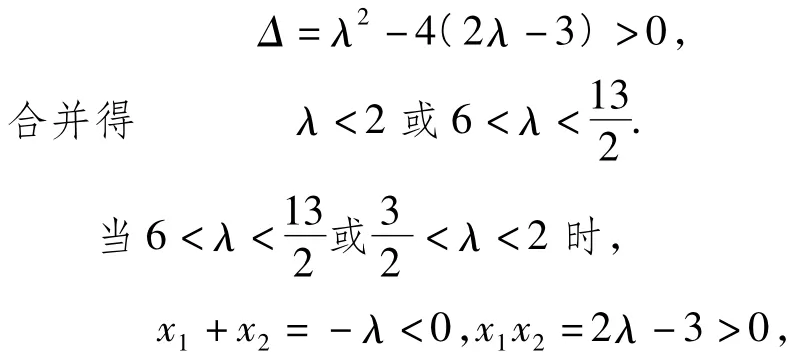
从而x1，x2均小于0.此时，命题等价于0＞f(－4)，于是符合题意.

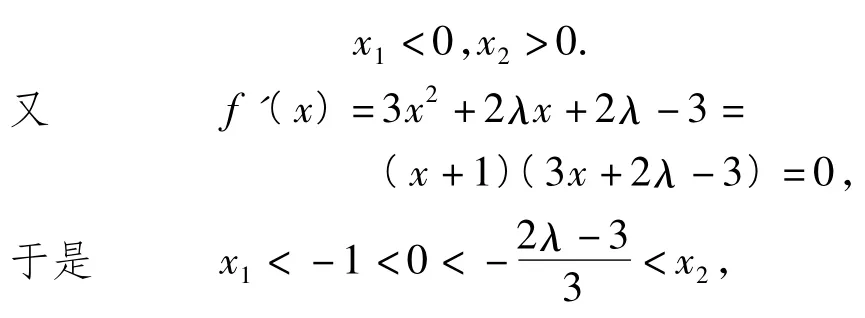
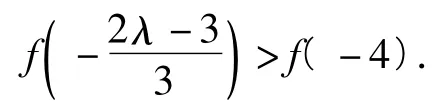
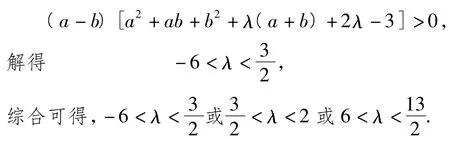
分析本题是2014年浙江省数学学业水平考试压轴题，难度系数为0.25.大多数学生不善于分析题意，不能通过特殊情形，缩小讨论范围，而是机械地对a进行分类讨论，导致失败.事实上，只要优先考虑f(x)=x|2x－a|的图像便不难发现f(x)在上递增，在上递减，在上递增.因此符合题意的a必须满足

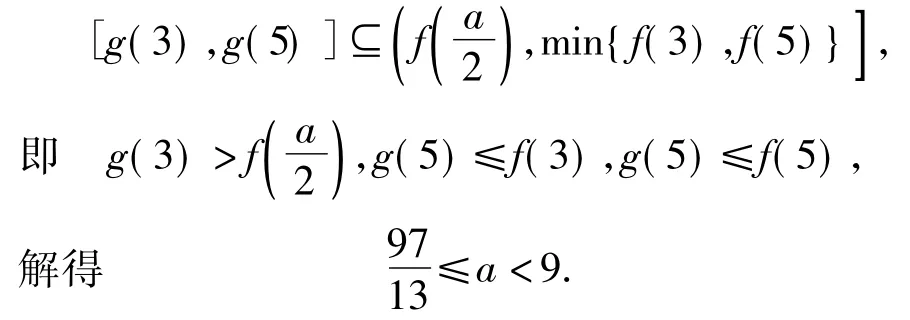
当12＜a＜20时，g(3)＜0，而f(x)在［3，5］上非负，无解.

点评对于一些运动变化的问题，我们也可以优先考虑某个特殊情形下的求解，如立体几何中双动点问题，因此解题时要善于使用该策略.

4 挖掘内隐条件优先

一道综合题常常内隐了许多的限制条件，需要解题者细心观察，如二次曲线上点的变化范围、三角函数的有界性、判别式的正负性等等，解题稍不留意就会出错.因此，解题时要优先考虑试题中的内隐条件，避免走弯路.

例6在△ABC中，角A，B，C所对的边分别为a，b，c，已知sinA+sinC=psinB(其中p∈R)，且.若角B为锐角，求p的取值范围.

分析本题是2011年浙江省数学高考题，它内隐的条件有2个:一个是在“a，b，c能构成三角形”的前提下，“角B为锐角”等价于“cosB＞0”，也等价于“a2+c2－b2＞0”;另一个是在“sinA+ sinC=psinB(其中p∈R)”中内隐了p＞0.实际考试时，绝大多数学生疏于隐含条件的挖掘，通过正、余弦定理转化成(误认为cosB＞0或p∈R)致错.

例7设a，b∈R，已知函数f(x)=alnx+x2+ bx存在极大值，求a的最大值，使得对于b的一切可能取值，f(x)的极大值恒小于0.

解延用分析中的表述，f(x)的极大值为构造函数g(x)=alnx－x2－a.当时，

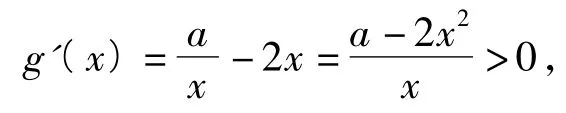
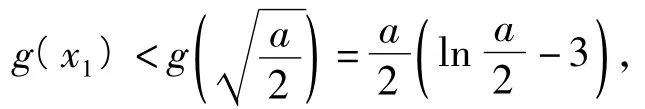
于是，当0＜a≤2e3时，

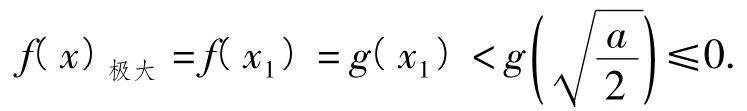
而当a＞2e3时，取，即

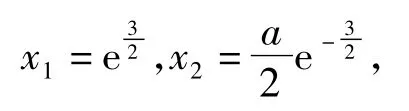
不符合题意.综上所述，a的最大值为2e3.

5 命题转换优先

有些数学综合题从表面形式来看，难以发现其本质，但通过换元引参，改变题目的呈现方式，就可将其化归为平时熟悉的问题，解题思路也会一目了然.

分析令cosθ=x，sinθ=y，将原命题等价转换成一个线性规划问题.即ay+bx≥0，ax－by≥0，x2+y2=1(其中a，b都是不为0的常数)，求y的最大值.

例9已知数列{an}是等差数列，且a1∈［0，1］，a2∈［1，2］，a3∈［2，3］，则a4的取值范围为()

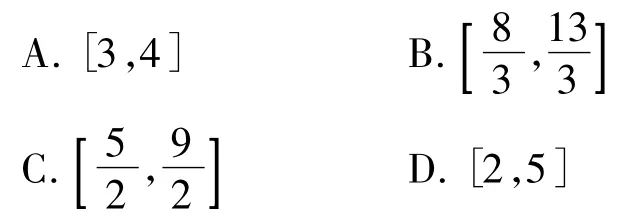
分析本题是2013年浙江省高中数学会考题，难度系数是0.45.该题表述形式是数列问题，但设首项a1=x，公差为y，命题就等价转化为一个线性规划问题:已知求a4=x+3y的值.经解答不难得正确选项是C.

6 目标分析优先

对照目标解题，是宏观上的引领，解题方向的把握.有些综合题只要根据总目标，选择适当的方法和途径，将已知条件进行优化组合与变形、化简与整理，就能不断向题设目标接近，从而实现解题.

例10如图3，若有且仅有一个正方形，其4个顶点均在曲线y=x3+ax上，求实数a的值及此正方形的面积.

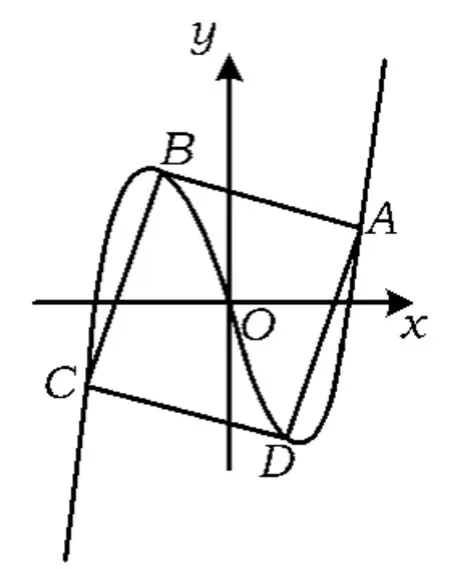
图3

分析本题是2013年浙江省课堂教学评比教师专业素养测试题.解题目标是求实数a，使曲线y=x3+ax上存在4个顶点均在曲线上的正方形，而且是唯一的.设正方形的4个顶点依次为A，B，C，D，则正方形ABCD的中心为原点，否则，由于曲线y=x3+ax为奇函数，因此，A，B，C，D关于原点的对称点A'，B'，C'，D'也在此曲线上，且四边形A'B'C'D'也是正方形，与题设矛盾.

不妨设OA的直线方程为y=kx(其中k＞0，点A在第一象限)，代入y=x3+ax解得点A的横坐标为

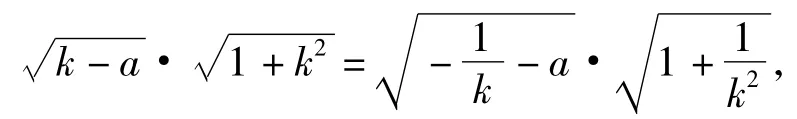
张金良，男，浙江海盐人，中学高级教师，浙江省第七批特级教师，浙师大、杭师大教育硕士兼职导师，全国第七届“苏步青数学教育奖”二等奖获得者，全国首届优秀教育硕士，浙江省劳动模范，现任浙江省教育厅教研室高中数学教研员，中国教育学会中学数学专业委员会理事、学术委员会委员，全国数学教育学会常务理事，浙江省普通高中新课程实验数学专业指导小组组长，浙江省教育学会数学教学分会副理事长兼秘书长，浙江省数学会常务理事、中学教学专业委员主任，浙师大数理学院基础数学教学研究所兼职副所长.在《数学通报》、《中学教研(数学)》等全国公开发行的专业刊物上发表论文80余篇，主编合编《普通高中数学新课程案例研究》、《高中数学必修知识拓展与引申》、《成人高中数学教材》等专业书刊30多册，出版《三角函数》编著1部，主持或参与国家、省、市级研究课题10项，获省政府基础教育教学成果奖1项，主要从事高中数学教学研究.