用于微振动控制的隔振器分析和实验

马俊

（四三一厂军代表室，辽宁 葫芦岛 125004）

用于微振动控制的隔振器分析和实验

马俊

（四三一厂军代表室，辽宁 葫芦岛 125004）

首先从隔振系统频响函数出发，得到系统最优频响表达式，然后根据最优频响条件，设计了一种用于微振动控制的隔振器，并通过实验测试隔振器的特性，获得了由隔振器和不同质量元件构成的系统的振动加速度和振动传递率。实验与理论计算结果一致性较好，说明设计是正确的。

振动与波；隔振器；微振动；最优频响；波纹管

微振动是影响高精度遥感卫星指向精度和成像质量等关键性能的主要因素，由于其微小性、固有性、宽频性和难控性，航天器的微振动力学环境极为复杂和特殊，分析与控制难度都很大。在实际中，两参数隔振器常被用与微振动隔振，主要因为其具有工作稳定、成本低、可以抑制共振峰等特点，但是研究也表明，两参数隔振器在隔振区的衰减率仅为20 dB，而且对高频干扰（如100 Hz以上的振动），隔离效果并不理想。因为隔振器存在驻波效应，随着频率的增高，高频区会出现一系列波峰，从而削弱隔振效果。在被动隔振中，一般通过增加隔振级数来提高隔振器的隔振性能，其中双层隔振系统最常用。一种特殊的两级隔振——Zerner隔振，在隔振区具有40 dB的衰减率。两级隔振的优点是可以获得更高的频率衰减特性，但其设计较困难，结构较复杂，而且较难获得最优值[1]。

对于Zerner隔振，国外研究较早，如LIN Y等人对由膜片泵弹簧和阻尼构成的系统进行分析[2]；Davis P在卫星隔振平台中采用了Zerner隔振器，并对其原理进行了简单阐述[3]；Davis L P在前人工作的基础上，总结了Zerner隔振和两参数隔振的优缺点[4]。Davis T在多轴主被动混合隔振中采用了隔振器，从而使平台具有更低的隔振频率[5]。Wilson研究了在D-strut结构上采用Zerner隔振和两参数隔振的隔振效果[6]。

本文在隔振器机理与参数分析的基础上，提出一种Zerner隔振器，并通过实验研究了其对微振动的隔离效果及参数依赖性。

1 隔振器系统模型分析

考虑图1所示的隔振模型，其振动方程为

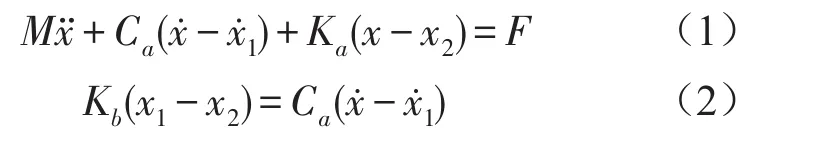
其中M表示质量，Ca是阻尼，Ka为平行主刚度，Kb为串联刚度。

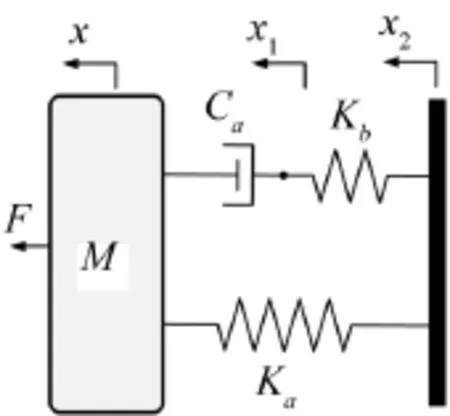
图1 隔振模型

对方程（1）两边求导

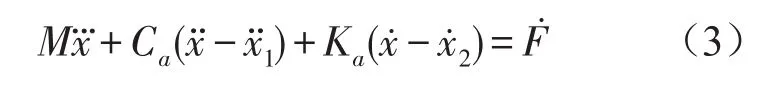
综合方程（1）、（2）、（3），得到方程（4）

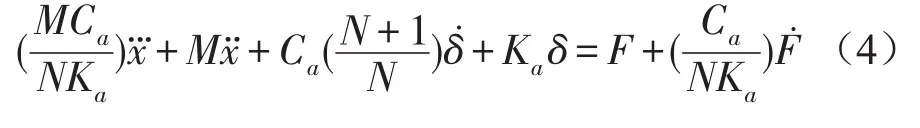
其中假设Kb=NKa，δ=x-x2，N为刚度比。

对方程（4）两边同时进行傅里叶变换，可以得到传递函数[5]

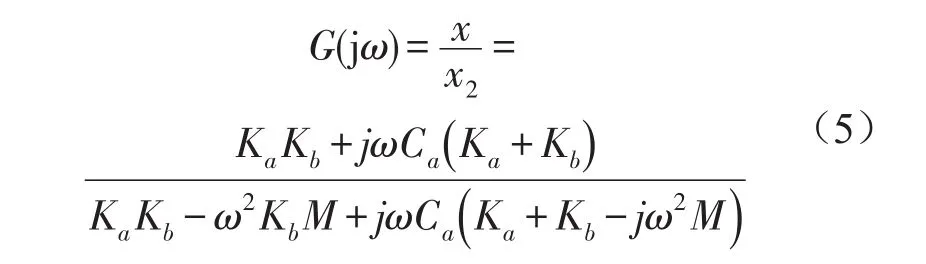
当系统输入为基础激励时，通过方程（4）也可以得到频响函数的另一种形式[1]

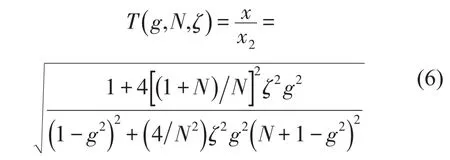
其中g为频率比，ζ为阻尼比。

式（6）以参数N为常数，参数（ζ，g）为变量求解隔振系统频响函数最优值得[3]

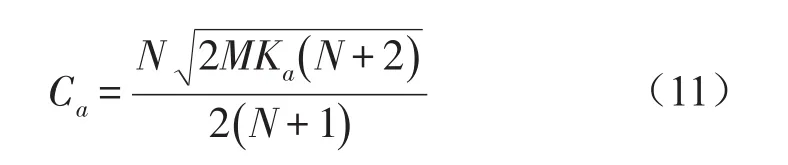
式（9）中的ω可利用式（10）和（11）进一步简化，只包含隔振器参数

式（13）是隔振系统在最优阻尼下的共振频率表达式。

2 隔振器设计和实验

隔振器结构如图2所示，实物如图3所示。

图2 隔振器结构图

图3 隔振器实物图

隔振器的刚度元件选取波纹管，由图2可以看到，零件1和2之间的波纹管相当于理论模型中Kb，零件3和5之间的波纹管相当于理论模型中的Ka，Ca阻尼是由阻尼孔和黏滞流体流动产生。

波纹管的厚度是变化的，实测波峰处厚度约为0.10 mm，波谷处厚度约为0.15 mm，波纹管内圆环壳的厚度，可利用经验公式得到近似值。黏滞流体采用的是水，在25°时它的标准运动黏度是1 cst[7]。

2.1 隔振器刚度特性

利用MTS电液式万能试验机（50 kN）分别对28个波的波纹管和隔振器的主刚度进行测试，图4为刚度测试图。

图5为波纹管的力—位移曲线，由图可以看出，波纹管的刚度具有线性特性。由轴向变形（10 mm）和轴向力（约为42 N）可以计算出半波的实际刚度

图4 利用试验机测试刚度图

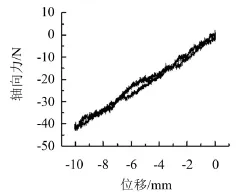
图5 U型波纹管力位移曲线

图6是隔振器主波纹管的力—位移曲线，由此可以计算出主波纹管的刚度Ka

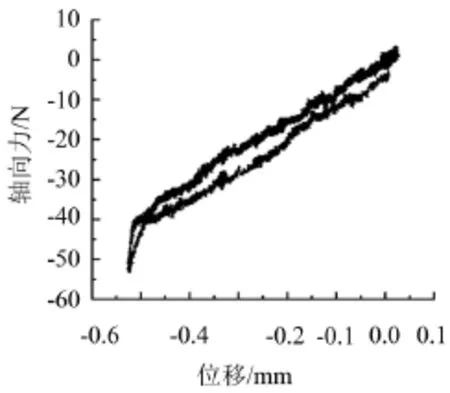
图6 主波纹管力—位移曲线

由式（16）计算可知，隔振器的主波纹管相当于两个具有3个波的波纹管并联，m表示主波纹管的波数，这与实际结构相符

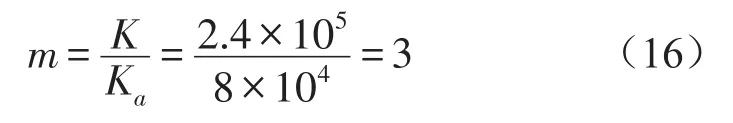
式（14）、（15）和（16）表明实测结果比较准确，利用相同方法，可以得到Kb

2.2 隔振器的传递特性测试

测试系统如图7a所示，包括电磁激振台、加速度传感器和数据采集仪等，图b为隔振器和质量块在激振平台安装方式以及两个加速度传感器的安装位置。

测试原理如图7a所示，采用基础激励，通过两个加速度传感器的测量信号得到单级隔振的频响函数。

图7 隔振系统位移传递率测试原理图

在电磁振动台上进行隔振器的传递特性测试。首先，测试仅有主波纹管的隔振系统的传递特性，结果如图8所示，共振频率为22.0 Hz，共振峰值约为48 dB，隔振系统的阻尼很小。其次，分别用4 kg、6 kg、15 kg、17 kg、19 kg、25 kg的质量块与隔振器一端联接，隔振器另一端安装在水平振动台面上，使之组成一个隔振系统。振动台激励为1 Hz～200 Hz范围内正弦扫描，分别采用了降频和升频两种模式，并且进行了重复性验证。隔振器的加速度传递特性如图8所示，由图中可以看出，随着质量的增大，共振峰向左侧移动，峰值先降低再增大[10，11]，其中实线为阻尼器自身无阻尼时的频响函数。

隔振器存在两个共振频率，其物理意义的分析可以从结构入手，如图1所示，当结构中阻尼为0时，整个系统只有Ka起作用，系统的固有频率计算方程如式（18），定义为第一固有频率，当结构中的阻尼为无穷大时，Kb和质量相当于刚性连接，整个系统简化为Ka和Kb并联，系统的固有频率计算如式（19），定义为第2固有频率。

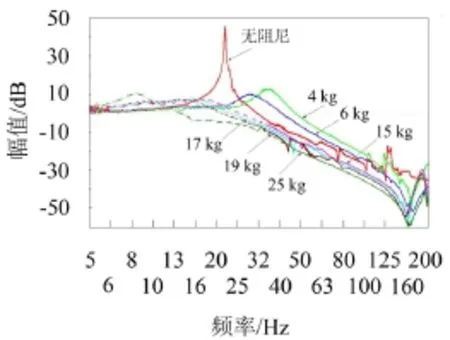
图8 不同隔振质量的加速度传递特性曲线

图8中的数据与表1对应，表1中数据包括不同质量下隔振系统的第1和第2固有频率，可以看出，实际的共振频率都处在第1和第2固有频率之间，随着质量的增大，共振频率从第2固有频率向第1固有频率靠近，同时在这个过程中会出现最优阻尼比的特殊情况。表1也给出了共振幅值，质量变化时，T也不断变化，但是从表中可以得到隔振系统的Tmin最小值约为2.2，这时系统的输出阻尼达到最优值。

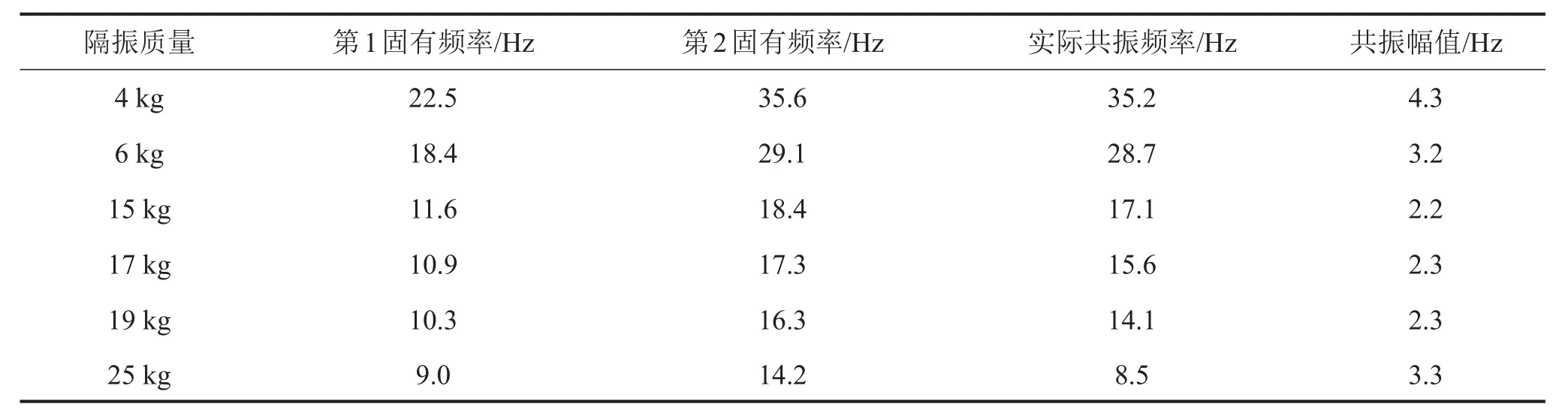
表1 不同隔振质量下系统的固有频率的理论值与实测值

由公式（7）可以知，此时隔振系统的理论峰值应为

其中N为刚度比，隔振器的实际刚度比约为1.5，代入式（20）可得，T=2.3。由此可以看出，理论结果与实验结果吻合良好。

通过理论分析可知，隔振系统负载质量取一个确定的值时，隔振系统会取到最优阻尼，但是在实际应用当中，在满足设计要求前提下，系统的负载质量并不需要完全和理论值精确相等，只要在一个范围之内即可，从表1中可证实这个想法，可看出当质量从4 kg～25 kg递增时，系统振幅变化规律是从大到小，然后再变大。

假定阻尼器设计要求中规定振幅范围是不大于2.3时，通过表1可以知道，只要负载质量在15 kg～19 kg之内，所设计的隔振器就满足要求。

3 结语

本文得到隔振系统在最优阻尼比下的共振频率表达式。实验测试与理论计算结果相符，说明隔振器设计有效。隔振器在共振峰处的放大因子可以按公式预估。

[1]丁文镜.减振理论[M].北京：清华大学出版社，1988.

[2]Lin Y,Cunningham D.Stiffness and stress of a fluid-filled circular diaphragm[J].AIAAjournal,1992:1504-1513.

[3]Davis P,Cunningham D,Harrell J.Advanced 1.5 Hz passive viscous isolation system[C].Proceeding of the 35 th AIAA/ASME/ASCE/AHS/ASC Structures.Structural Dynamics and Materials Conference.America:1994.2655-2665.

[4]Davis L P,Carter D R,Hyde T T.Second-generation hybrid D-strut[J].International Society for Optics and Photonics,1995:161-175.

[5]Davis T,Davis L P,Sullivan J M,et al.High-performance passive viscous isolator element for active/passive(hybrid)isolation[C].Symposium on Smart Structures and Materials.International Society for Optics and Photonics. Amecria:1996.281-292.

[6]Wilson G W,Wolke P J.Performance prediction of D-Strut isolation systems[C].Smart Structures and Materials 97 International Society for Optics and Photonics.America: 1997.236-250.

[7]刘德金.波纹管液压成形工艺的设计计算[J].仪表技术与传感器,1976,2(2):44-49.

Analysis and Experiment of Isolators for Micro-vibration Control

MA Jun
（Military Representative Office in 431 Factory,Huludao 125004,Liaoning China）

The expression of the optimal frequency response of an isolation system was obtained through the analysis of its frequency response function.Based on the result,an isolator for micro-vibration control was designed and its performance was tested.Vibration acceleration and minimum transmissibility rate of the isolation system with different mass components and the isolator were measured.The test results were in a good accordance with those of calculation,which indicate that the design of the isolator is correct and effective.

vibration and wave;isolator;micro-vibration;optimal frequency response function;bellows

TB535+.1

A

10.3969/j.issn.1006-1335.2015.02.045

1006-1355(2015)02-0205-04

2014－10－29

马俊（1979－），男，辽宁辽阳人，海军驻葫芦岛431厂军事代表室，工程师，从事舰船的监造工作。E-mail:hhj@sjtu.edu.cn