显式积分求解橡胶元件刚度的方法研究

李海涛，周相荣，李 佳，王 强

(上海船舶设备研究所 减振中心,上海 200031)

显式积分求解橡胶元件刚度的方法研究

李海涛，周相荣，李 佳，王 强

(上海船舶设备研究所 减振中心,上海 200031)

应用显式积分与隐式积分两种求解方法计算橡胶元件的垂向静刚度，其中显式积分采用斜坡、正弦、光滑三种加载函数进行位移加载。通过对比分析计算结果与试验数据发现，其中斜坡加载的动能在计算初始时出现振荡，而光滑加载与正弦加载的动能整个过程均并没有出现振荡；在大变形时，隐式积分求解方法由于出现网格畸变从而导致程序收敛失败，此时显式积分求解体现出优势，并且三种加载函数的计算结果几乎无差别，并且与试验数据吻合度比较好，最大误差为5.7%。对于橡胶元件大变形问题，应用显式积分求解静刚度的方法是可行的，并且不同的加载函数会直接影响计算结果，尤其是在初始计算阶段的结果的准确性有很大的影响。

振动与波；橡胶元件；大变形；静刚度；显式积分；加载函数

橡胶是一种在外力作用下能发生较大的形变，并且当外力解除后又能迅速恢复其原来形状的有机高分子材料，在工程上广泛用于制作减振降噪元件，如发动机减振器、机器支座、橡胶金属悬挂元件等。静刚度是橡胶元件设计时首先需要满足的技术参数，能够准确地预测其静刚度特性曲线，对后续开发是否成功起到关键性作用。

橡胶材料应力—应变关系是具有高度非线性的弹性，这种材料行为称为超弹性。超弹性材料在大应变值时，依然保持弹性，所以在计算橡胶元件的刚度尤其是在大变形时，要考虑到橡胶的超弹性，利用隐式积分求解橡胶元件非线性刚度时，会因大变形造成网格过度畸变或体积自锁从而导致程序收敛失败[1,2]。大变形问题的网格设计非常困难，设计网格时必须使单元形状在整个分析中是合理有效的。对于网格大变形的静态求解问题可以应用显式积分方法求解，并且用显式求解方法不会出现存在收敛问题，相对隐式算法的静态求解更容易一些，并且当遇到大模型时，显式也比隐式求解对系统资源的占有率较低，但是采用显式求解方法需要解决的两个重要问题是准静态加载函数和加载时间的选择。使用了显式积分方法，不可避免地引入了动能，但是在准静态加载过程中,若是内能光滑地变化，而不会有太大振荡，并且动能在加载结束后能够很快收敛于0，则认为此准静态过程模拟质量很高[3,4]。国内，有学者通过选取适当质量缩放因子和采用材料的黏性阻尼来提高橡胶弹簧垂向静刚度的显式分析计算效率[5]。

本文应用隐式积分与显式积分两种方法计算某型号橡胶元件的垂向静刚度，其中显式积分采用斜坡、正弦、光滑三种加载函数进行位移加载，研究了斜坡加载、光滑加载与正弦加载对显式积分准静态过程的影响，并将计算结果与试验数据进行对比分析，分析在大变形下显式积分、隐式积分求解橡胶元件静刚度的优劣，得出了一些结论，供工程应用参考。

1 显式积分求解静态问题的基本原理

在求解静态问题时，利用隐式积分求解方法，常常会因材料大变形，造成网格过度畸变或体积自锁从而导致程序收敛失败，此时可以通过显式积分求解方法模拟准静态求解静态问题，并且用显式求解方法不会出现存在收敛问题，相对隐式算法的静态求解更容易一些，并且当遇到大模型时，显式也比隐式求解对系统资源的占有率较低。

显式求解方法是真正的动态求解过程，其最初是为了模拟高速冲击问题而设计的。动态问题相对于静态问题在求解过程中最大的不同是：惯性力发挥了主导性作用。所以将显示动态过程应用于准静态问题求解时，需要降低惯性力，并且使其对整个分析过程的影响可以忽略。但是降低惯性力会直接增加加载时间，所以在应用准静态分析方法时，要在尽量降低惯性力影响的状态下用最短时间进行模拟。

对于一个准静态过程在其自然时间内进行分析，一般均可以得到准确的静态结果，但是若是按照自然时间计算整个过程则计算代价会非常大。在静态分析过程中，结构的最低阶模态通常控制着结构的响应，一般理想的是加载时间为最低阶模态周期的10倍，以确保整个求解过程为真正的准静态。对于准确、高效的准静态分析要求施加的载荷尽可能光滑，任何突发的运动均会产生应力波，并且导致分析过程振荡，结果不准确。光滑的加载方式是指加速度从一个增量步到下一个增量步只能改变一个相对小量，则其速度、位移也是光滑的。在数学上则表示为该加载曲线及其1阶与2阶导数均是光滑的。

本文采用三种加载方式进行位移加载：斜坡加载、光滑加载与正弦加载，加载函数如式(1)—式(3)所示，式中，t0为准静态加载结束时间，t为时间，x0为加载的位移值，x(t)为位移x0的准静态加载函数。

斜坡函数

2 有限元模型的建立

本文设计的橡胶元件主要由弹性装置与质量环组成，质量环与弹性装置通过螺栓紧固连接（如图1），弹性装置主要由内环与外环通过橡胶硫化组成，橡胶元件垂向最大变形量为10 mm。结构中橡胶材料的应力—应变曲线如图2所示，并且橡胶材料采用Yeoh超弹模型进行模拟。超弹理论认为材料具体一种与应变率无关的非线性弹性特性，该类材料应力—应变关系可以用单位体积应变能来度量[6]，如式(4)。

图1 橡胶元件

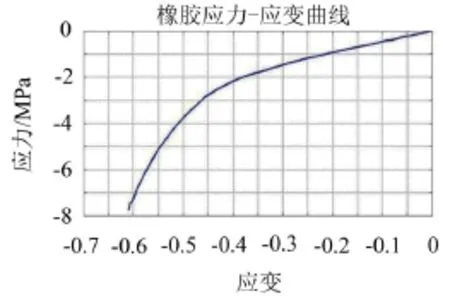
图2 橡胶应力—应变曲线

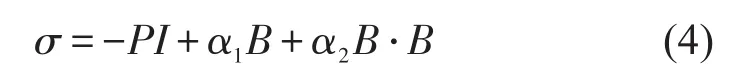
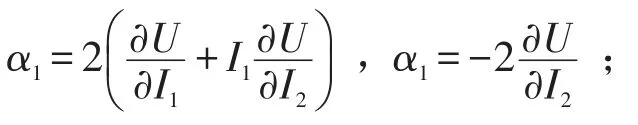
Yeoh[7]通过分析应变能函数，忽略掉对应变能影响小的I2，将应变能函数简化为I1的函数，完整的Yeoh模型表示为I1的三次多项式。式(5)应变能中的系数C10、C20、C30需要通过材料静态单向拉、压，剪切等试验确定。一般受试验条件限制，通常橡胶材料试验只做单向压缩、拉伸试验，而Yeoh模型的好处是仅依靠单向拉、压试验数据就可以比较好地预测剪切等其它复杂的材料行为

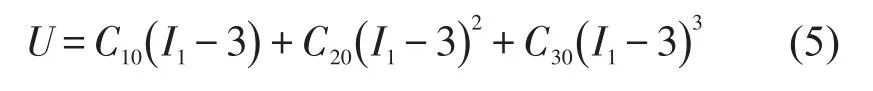
将图1所示的橡胶元件三维模型进行适当简化处理，将不影响结构特性但是会影响网格质量的如螺栓孔、凸台、倒角、螺栓、平垫片等结构省去，并将简化后的模型导入Abaqus内，作为计算模型，并对其划分六面体网格，如图3所示。实际中，质量环与弹性装置是通过螺栓进行紧固连接的，并且变形是发生在橡胶部分，所以可以通过绑定（Tie）接触将质量环与弹性装置固定。弹性装置的橡胶与内外环是通过硫化固连在一起的，可以通过绑定（Tie）接触进行模拟。将橡胶元件的内环通过耦合（Couple）约束到参考点2（RP-2），对参考点2施加位移载荷；质量环上表面区域通过耦合（Couple）约束到参考点1（RP-1），用位移约束进行固定。

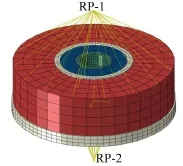
图3 橡胶元件有限元模型

本文采用隐式积分与显式积分两种方法计算橡胶元件的垂向静刚度，其中显式算法采用式（1）—式（3）所示的三种加载方式进行10 mm的位移加载，三种位移加载曲线如图4所示。并且应用显式积分求解橡胶元件垂向静刚度时，对其垂向结构响应影响最大的是垂向第1阶模态。通过计算得知橡胶元件的垂向第1阶模态频率为50 Hz，所以在计算橡胶元件时，加载时间为0.2 s。

图4 加载曲线

3 计算结果分析

3.1 三种加载函数对显示积分准静态的影响

在查看橡胶元件静刚度数值前，应该确定整个分析过程是否为准静态。在橡胶元件受压的过程中，内能主要是由于橡胶变形所产生的，而动能则是内环运动所产生的，所以可以比较整个模型分析过程的内能与动能历史。为了确定整个过程为一个准静态过程，动能应该不超过内能的5%～10%，并且整个过程的动能还要满足不能振荡，若是在光滑加载的情况下却出现振荡的能量结果，则计算结果是不合理的。

图5为三种加载函数橡胶元件准静态过程的动能与内能历史对比曲线，动能与动能历史对比曲线，从前三个内能与动能对比可以看出，三种加载方式在整个准静态过程动能均远远小于内能，但是三种加载方式的动能在整个过程却并不相同，其中斜坡加载的动能出现振荡，并且在完成加载后动能也没有收敛于0；而光滑加载与正弦加载的动能整个过程均是光滑地增大与光滑地减小，没有出现振荡，并且正弦加载的动能最大值也要小于光滑加载的30%。所以从对比动能与内能的方面，光滑加载与正弦加载的准静态过程的模拟准确性要好于斜坡加载形式，光滑加载与正弦加载的计算结果相对于斜坡加载是更可靠的。

3.2 计算结果与试验结果对比分析

将应用显式积分、隐式方法求解得到的橡胶元件的力—位移曲线与试验测得的力—位移曲线绘制在同一坐标系内，如图6所示，隐式积分求解橡胶元件的静刚度时，仅能计算到加载位移为5 mm，加载位移大于5 mm后便会出现网格畸变从而导致程序收敛失败，所以对于变形量大于5 mm后，隐式积分算法失效。

图6 橡胶元件力—位移曲线对比

图5 三种加载方式能量对比

在变形量为0～0.5 mm，斜坡加载函数的计算结果明显大于试验数据、光滑加载、正弦加载与隐式积分求解的结果，与试验数据最大误差为62.1%，而这主要是由于斜坡加载方式在计算初始时，动能出现明显波动造成的，如图5所示，而另外两种加载函数的计算结果与实验数据的误差均小于4%；在位移加载到1 mm以后，三种加载函数求解的力—位移曲线几乎一致，主要是加载到1 mm以后三种加载过程的动能均不存在振荡现象，并且远远小于内能的5%。由图6所示可知，针对橡胶元件应用隐式积分与显示积分（在位移为0～1 mm部分排除斜坡加载方式的计算结果）这两种方法计算得到力—位移曲线在位移为0～5 mm内重合度很好。在位移为0～2 mm，显式与隐式求解的力—位移曲线几乎重合；在位移为2 mm～5 mm，显式与隐式求解的力—位移曲线逐渐存在误差，具体表现为：显式求解的力—位移曲线在相同位移对应的力的逐渐小于隐式求解的，并且试验获得的力—位移曲线在介于两者之间。在位移为0～5 mm内，隐式积分计算结果与试验结果最大误差在位移为5 mm处，为1.8%；显式积分计算结果与试验结果最大误差也是在位移为5 mm处，为4%。在位移为5 mm～10 mm时，由于网格畸变从而导致隐式积分收敛失败，此时只能应用显式积分求解，显式积分计算得到力—位移曲线与试验数据随着位移的增加误差不断增大，最大误差达到5.7%，而造成产生这种误差的原因是在橡胶在高度变形状态下，橡胶的自由面进一步减少，而显式积分中的体积压缩模型无法精确模拟这一高度变形工况。对于橡胶元件大变形问题，显式积分求解的力-位移曲线与试验数据吻合度比较好，所以在最初设计时应用显式积分求解静刚度的方法是可行的。

4 结语

应用显式积分与隐式积分两种求解方法计算橡胶元件大变形下的静刚度，其中显式积分求解时采用斜坡、正弦、光滑三种加载函数进行位移加载。在小变形时，光滑加载与正弦加载的计算结果相对于斜坡加载是更可靠的，与隐式求解的结果、试验数据吻合度很好；在大变形时，隐式积分求解方法由于出现网格畸变从而导致程序收敛失败，此时显式积分求解体现出优势，三种加载函数的计算结果几乎无差别，并且与试验数据吻合度比较好，最大误差为5.7%。所以对于橡胶元件大变形问题，应用显式积分求解静刚度的方法是可行的，并且不同的加载函数会对计算结果，尤其是在初始计算阶段的结果有很大的影响。

[1]庄 茁，由小川.基于ABAQUS的有限元分析和应用[M].北京：清华大学出版社，2009.

[2]刘立忠，刘相华.隐式静力和显式动力有限元在轧制过程模拟中的应用[J].塑性工程学报，2001，8(4)：81-83.

[3]黄志辉，陈盛钊，柏友运.显式准静态几种加载方法的讨论[J].武汉理工大学学报，2006，33(6)：122-125.

[4]樊建平，章建军，陈传尧.用显格式技术对复杂结构准静态加载的有限元模拟[J].计算力学学报，2002，19(4)：431-437.

[5]张亚新，黄友剑，程海涛.显式积分技术求解橡胶元件大变形问题的研究及应用[J].铁道机车车辆，2013，33(6)：15-18.

[6]匡振邦.非线性连续介质力学[M].上海：上海交通大学出版社，2002.

[7]Yeoh O H.Some forms of the strain energy function for rubber[J].Rubber Chemistry and Technology,1993,66: 754-771.

Study on Explicit Integration Used for Solving the Stiffness of Rubber Element

LI Hai-tao,ZHOU Xiang-rong,LIJia,WANG Qiang
(Shanghai Marine Equipment Research Institute,Shanghai 200031,China)

The vertical static stiffness of rubber element is solved by the explicit integration and implicit integration, and three loading functions including ramp,sinusoidal and smooth function,are chosen in explicit integration.It is indicated by simulation analysis and experimental results that the kinetic energy of ramp function exists the oscillation,while the kinetic energy of smooth and sine function exists the no oscillation during the initial step time.In the large-strain,implicit integration is failing because of mesh distortion,then the explicit integration is high-efficiency and the simulation results are consistent with experimental results,the maximum error is 5.7%.It is efficient that the explicit integration is used for solving the large-strain stiffness of rubber element and the different loading functions affect the simulation results directly,especially during the initial step time.

vibration and wave;rubber element;large strain;static stiffness;explicit integration;loading function

O422.6

A

10.3969/j.issn.1006-1335.2015.02.046

1006-1355(2015)02-0209-04

2015－01－10

作者信息：李海涛(1989－)，男，辽宁朝阳人，硕士研究生，研究方向为设备振动噪声控制。E-mail:leewaver@163.com