空滤器结构优化和辐射噪声分析

彭卓凯，邓志强，黄振邦

（大长江集团 研发中心，广东 江门 529030）

空滤器结构优化和辐射噪声分析

彭卓凯，邓志强，黄振邦

（大长江集团 研发中心，广东 江门 529030）

针对试验中发现的空滤器壳体辐射噪声大问题，综合运用模态计算、进气压力频谱计算、拓扑优化、形貌优化和声学有限元法解决了该问题。首先，通过模态计算，得出了空滤器外壳的各阶振型和模态频率。接着分析了发动机的进气压力波频谱，找出了进气压力较大的频段，由此可知空滤器辐射噪声大是由于第1阶频率较低引起的。然后，通过拓扑优化和形貌优化，找出了筋的最佳布置位置，使空滤器外壳的第1阶频率得到大幅提高。最后，通过辐射噪声的计算，确认了改进后的空滤器外壳的总声功率级降低了13.8 dB，噪声改进效果非常明显。

声学；空滤器；进气压力；优化；辐射噪声；有限元法

摩托车空滤器是发动机进气系统的一个重要组成部分，其作用是预先对进入气缸的空气过滤，防止灰尘或沙粒进入气缸，以减少气缸、活塞、活塞环的磨损，延长发动机的工作寿命。在现代摩托车的空滤器结构设计中，还注重进气消声；另外，空滤器还具有优化匹配发动机性能的作用[1,2]。

空滤器大体由两部分组成：空滤器壳体和滤芯。为了达到较好的滤清效果和减少过滤时对空气的阻力以及增大储灰能力，空滤器应设计得尽量大一些。但当空滤器较大时，在进气压力波的激励下，空滤器壳体容易发生共振而发出较大的噪声。某空滤器在试验过程中被发现其外壳体辐射噪声较大，此时，发动机转速在6 000 r/min左右。现本文综合运用模态计算、进气压力频谱计算、拓扑优化、形貌优化和声学有限元法来解决该问题。

1 空滤器模态计算

试验时出现共振的空滤器外壳体如图1、2所示，该件通过6个安装点与空滤器内壳体组装在一起。为解决该共振问题，首先对空滤器外壳体进行模态分析。将在NX软件中建好的3D模型导入有限元分析软件Nastran中，进行网格划分，采用2 mm二阶四面体单元。接着定义部件的材料属性，材料为PP塑料，弹性模量为1 000 MPa，泊松比为0.41，密度为890 kg/m3。再定义边界条件，将6个安装孔约束住。最后定义模态提取分析步，提取1 000 Hz以前的所有模态。计算出的原始空滤器外壳的模态频率见表1，第1阶模态振型见图3，从该振型可知，中部的圆形区域振幅最大。从计算出的模态频率和振型看，第1阶模态频率较低是造成辐射噪声大的主要原因，因为在进气压力波的激励下，空滤器外壳会发生共振。为进一步验证该推断，下面进行进气压力频谱计算。

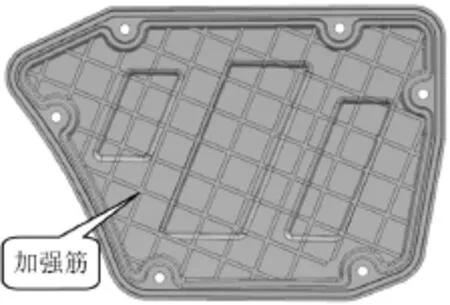
图1 原始空滤器外壳（里侧）

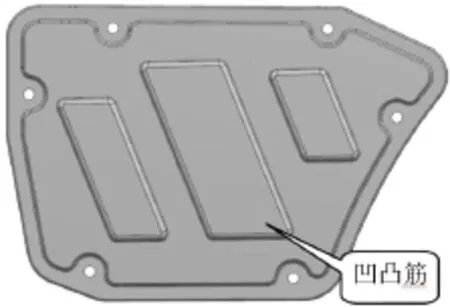
图2 原始空滤器外壳（外侧）

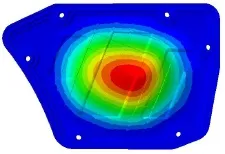
图3 原始空滤器外壳第1阶振型

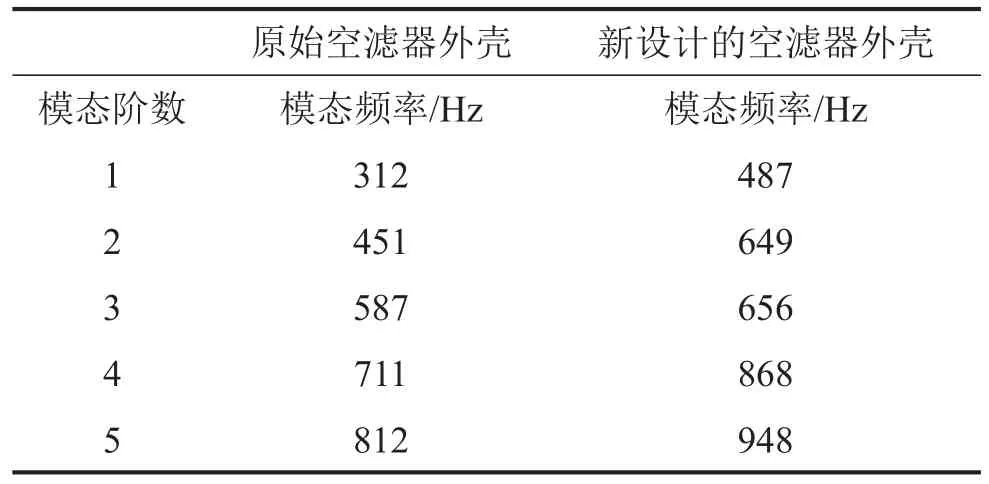
表1 改进前、后的空滤器外壳模态频率

2 进气压力频谱计算

该发动机为125 ml排量的单缸自然风冷发动机。在发动机模拟分析软件boost中，对该发动机进行建模，设置相应的进气系统、燃烧系统、排气系统等参数，在空滤器内设置压力监测点，测量发动机转速在6 000 r/min时空滤器内压力随曲轴转角的变化关系，并将此压力在时域内的信号通过快速傅里叶变换（FFT）转换为频域信号[3]。在6 000 r/min时，空滤器内压力的频谱如图4所示。

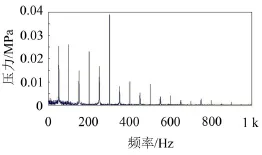
图4 空滤器内压力在6 000 r/min时的频谱

从该图可知，在300 Hz和低于300 Hz的区域，空滤器内压力较大，在高于300 Hz的区域，空滤器内压力随频率增加而逐渐减小。从上面的模态计算可知，空滤器外壳体第1阶模态频率为312 Hz，这个频率位于进气压力较大的频域范围附近，故而会出现共振而产生较大的辐射噪声。

3 拓扑优化和形貌优化

优化设计有三要素，即设计变量、目标函数、约束条件。设计变量是在优化过程中发生改变从而提高性能的一组参数。目标函数就是要求的最优性能，是关于设计变量的函数。约束条件是对设计的限制。目标函数、约束函数是从有限元分析中获得的结构响应。设计变量的选择依赖于优化类型。在拓扑优化中，设计变量是单元的密度，在形貌优化中，设计变量为形状扰动的线性组合因子[4]。拓扑优化能在给定的设计空间内寻求最佳的材料分布。形貌优化是一种形状最佳化的方法，即在板形结构中寻找最优的凹凸型加强筋的分布，与拓扑优化不同的是，形貌优化不删除材料。

从以上的模态和进气压力频谱分析的结果可知，空滤器外壳体第1阶模态频率低，从而出现了共振问题。故提高第1阶模态频率可解决该问题。从原始空滤器外壳体的3D模型看（见图1、2），其上面布置了大量的网状加强筋，且还带有3个四边形的凹凸筋。从提高模态频率的角度考虑，这些加强筋和凹凸筋的形状和位置未必是合理的。为了找到最佳的加强筋和凹凸筋的布置位置，现对空滤器外壳体进行拓扑优化和形貌优化，以提高其第1阶模态频率。其中，拓扑优化用于确定加强筋（增加材料的筋）的最佳布置，形貌优化用于确定凹凸筋（不增加材料的筋）的最佳布置。

将原始的加强筋和凹凸筋都去除，再用优化计算重新布置这些筋。优化计算的模型采用1 mm四边形壳单元，如图5所示，其中灰色区域为设计区域（可优化区域），边缘黑色区域为非设计区域。优化目标为第1阶模态频率最大。在拓扑优化计算中，加强筋高度设为3.5 mm。在形貌优化计算中，凹凸筋的深度设为3 mm，起筋角度设为60°。

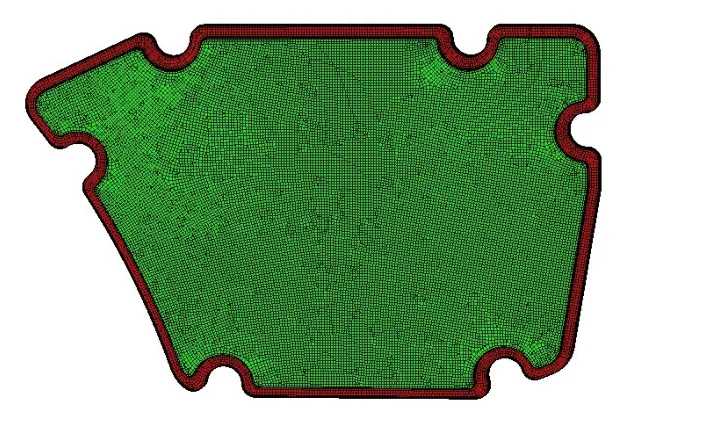
图5 空滤器外壳优化计算模型

形貌优化计算结果见图6，其中，除黑色以外的白色区域和灰色区域为最佳的凹凸筋布置位置。从图可知，凹凸筋应布置在外壳的中部，呈近似椭圆形。而原始空滤器外壳的凹凸筋为间隔一定距离的3个四边形，与优化结果有较大差异，这表明，原始凹凸筋的设计不尽合理。

图6 空滤器外壳形貌优化结果

拓扑优化计算结果见图7，其中，除黑色以外的灰色区域和接近灰色的白色区域为最佳的加强筋布置位置。从图可知，加强筋应布置在外壳的边缘，中间的大部分区域都无需布置加强筋。而原始空滤器外壳的加强筋呈网状密布，与优化结果差异大，这表明，原始加强筋的设计既浪费材料也不利于提高模态频率。

图7 空滤器外壳拓扑优化结果

现根据拓扑优化和形貌优化计算结果，对空滤器外壳的加强筋和凹凸筋重新设计，重新设计后的3D模型如图8所示。

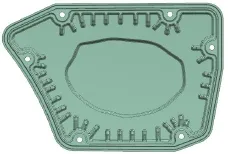
图8 重新设计后的空滤器外壳

4 空滤器辐射噪声计算

4.1 模态和动态响应计算

为进一步确认改进前、后的空滤器外壳的声学响应特性，现进行辐射噪声的分析。空滤器外壳在进气压力波的激励下，表面会产生振动，从而发出噪声。故首先须计算空滤器外壳表面的振动响应。对于带阻尼的多自由度系统，其受迫振动的微分方程为

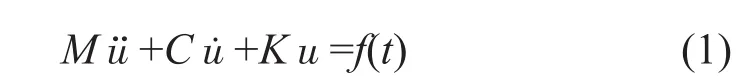
解这个运动方程一般有两种方法，一种是直接积分法，就是按时间历程对上述微分方程直接进行数值积分；另一种解法是模态叠加法[5,6]。对于计算系统在谐波激励下的线性响应，后一种基于模态的计算方法比直接积分的方法计算速度更快。故本文采用模态叠加法计算空滤器外壳表面的振动速度。首先须计算空滤器外壳的模态，再基于模态结果计算空滤器外壳在进气压力波激励下的振动速度。改进后空滤器外壳的结构有限元模型见图9，采用2.5 mm二阶四面体单元。改进前、后的空滤器外壳模态频率见表1，从该表可知，在不增加空滤器外壳基本壁厚的前提下，仅仅改变筋的布置，其第1阶模态频率已经由312 Hz大幅提高到了487 Hz。

图9 改进后空滤器外壳的结构有限元模型

4.2 辐射噪声计算

为求解流场中任意位置（x,y,z）处的声压p，可通过流体的连续方程、运动方程、能量方程、物态方程推导出Helmholtz声学波动方程，其表达式为[7]

∇2p(x,y,z)-k2p(x,y,z)=-jρ0ωq(x,y,z)

式中k为波数，ω为角频率，ρ0为定常流动下的密度，q体积速度。用数值方法求解Helmholtz方程的常用方法有声学有限元法（FEM）和声学边界元法（BEM）。当模型不是特别大时，有限元法在计算内声场和辐射噪声方面的速度更快，故本文采用有限元法。用有限元法求解Helmholtz方程时，首先需要把计算的声场离散成一定数量的小声场，每个小声场称为单元，单元之间用节点连接。对于三维声场，常用的单元有四面体单元和六面体单元。

本文采用3 mm四面体单元对空滤器外壳周围的声场进行离散，声学网格模型的截面图见图10。

并以空滤器外壳为中心布置半径为1 m的球面场点（见图11），以计算该球面场点上的辐射声功率。将上一步计算的空滤器外壳的表面振动速度导入声学计算软件LMS Virtual Lab，将表面振动速度映射到声学网格上作为辐射噪声计算的边界条件，求得改进前、后的空滤器外壳的辐射声功率如图12所示。从计算结果可知，原始空滤器外壳在312 Hz和739 Hz附近出现了声功率峰，312 Hz处的最大声功率级为127.2 dB。新设计的空滤器外壳在492 Hz和882 Hz附近出现了声功率峰，492 Hz处的最大声功率级为112.5 dB。对比模态计算结果可知，改进前、后的空滤器外壳的声功率峰都出现在第1阶和第4阶模态频率附近。原始空滤器外壳在整个频段的总声功率级为133 dB，新设计的空滤器外壳在整个频段的总声功率级为119.2 dB。总声功率级降低了13.8 dB；最大声功率级降低了14.7 dB。从以上辐射噪声的计算结果可知，噪声改进效果非常明显。

图11 球面场点

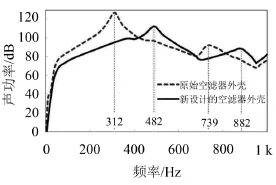
图12 改进前、后的空滤器外壳的辐射声功率

5 结语

（1）通过模态计算和进气压力波计算，得出了空滤器外壳的各阶振型和模态频率以及进气压力较大的频段，找出了空滤器外壳辐射噪声大的原因；

（2）通过拓扑优化和形貌优化，找出了筋的最佳布置位置，使空滤器外壳的第1阶频率得到大幅提高；

（3）通过辐射噪声的计算，进一步确认了空滤器外壳的改进效果：总声功率级降低了13.8 dB。噪声改进效果非常明显。

以上分析流程及相关的模拟计算方法为快速、准确地解决辐射噪声大问题提供了解决方案，减少了费时费力的试验，也节约了部件的材料成本（相对将部件简单的加厚的对策方案），对解决类似的车辆部件辐射噪声大问题具有一定的参考价值。

[1]冯超，邬惠乐.汽车工程手册摩托车篇[M].北京：人民交通出版社，2001.330-331.

[2]曾宪铮，吴振根.中外流行摩托车构造使用维修[M].长沙：湖南科学技术出版社，1996.164-165.

[3]朱访君，吴坚.内燃机工作过程数值计算及其优化[M].北京：国防工业出版社，1997.89-143.

[4]张胜兰，郑冬黎.基于Hyper Works的结构优化设计技术[M].北京：机械工业出版社，2007.159-163.

[5]许本文，焦群英.机械振动与模态分析基础[M].北京：机械工业出版社，1998.70-78

[6]刘延柱，陈文良，陈立群.振动力学[M].北京：高等教育出版社，1998.85-90.

[7]李增刚，詹福良.Virtual.Lab Acoustics声学仿真计算高级应用实例[M].北京：国防工业出版社，2010.4-17.

Structure Optimization and Radiation NoiseAnalysis of Air Cleaners

PENG Zhuo-kai,DENG Zhi-qiang,HUANG Zhen-bang
（Research&Development Center,Dachangjiang Group,Jiangmen 529030,Guangdong China）

Modal calculation,frequency spectrum calculation of intake pressure,topology analysis,topography analysis and acoustic FEM were employed to solve the serious radiation noise problem of an air cleaner’s shell.Firstly,vibration modes and eigen-frequencies of the air cleaner shell were obtained by modal computation.Secondly,the intake pressure spectrum was analyzed and the frequency zone with large intake pressure was determined.It was found that the large radiation noise of the air cleaner was resulted from the low 1st order frequency.Finally,the optimal position of the ribs was discovered by topology and topography analysis,so that the 1st order frequency of the air cleaner could be enhanced greatly. The result of the radiation noise computation show that the total sound power level of the air cleaner can be reduced by 13.8 dB after the modification and the improvement effect is very obvious.

acoustics;air cleaner;intake pressure;optimization;radiation noise;finite element method

TB53

A

10.3969/j.issn.1006-1335.2015.02.049

1006-1355(2015)02-0222-04

2014－10－17

彭卓凯（1979－），男，硕士，主要从事摩托车及其发动机的CAE和NVH分析。E-mail:pengzhuokai@126.com