一种可调频式的管路动力吸振器研究与实验验证

周 笛，陈 果，刘明华，罗 云，侯民利，刘彬彬

(1.南京航空航天大学 民航学院，南京 210016；2.成都飞机工业（集团）有限责任公司，成都 610092)

一种可调频式的管路动力吸振器研究与实验验证

周 笛1，陈 果1，刘明华2，罗 云2，侯民利2，刘彬彬1

(1.南京航空航天大学 民航学院，南京 210016；2.成都飞机工业（集团）有限责任公司，成都 610092)

基于反共振原理，设计了一种可调频式的管道动力吸振器，通过移动弹簧片上的质量块位置，并将其安装在管路共振位移最大处，可以实现不同频率下管道减振。通过构建了一段空间管路，利用有限元仿真分析和管道振动实验，验证了本文设计的调频动力吸振器能够在不同共振频率处对管路进行有效减振，结果表明调节减振器弹簧片上的质量块位置能够将减振器的减振效果调整到最佳。所研究的可调频式管道动力吸振器具有很强的工程应用价值。

振动与波；管道；振动抑制；动力吸振；调频；有限元分析

飞机液压管道主要用于输送燃油、液压油等介质，对飞机安全性的影响是不言而喻的。而管道振动问题一直是导致造成管道事故的主要原因之一。据有关文献记载[1]，在1965—1966两年中，某些歼击机由于导管及管接头故障而失事的次数占失事总数的60%。然而在这些故障中，大部分都是由振动引起的振动疲劳和振动磨损[2]。因此，对管道振动的控制就显得极为重要了。

对于管路振动抑制，主要分为主动抑制[3]和被动抑制[4]两种方式。被动抑制具有对环境依赖小，不需增加其他额外能量等特性，能更好的针对已设计好的复杂管路中出现的振动过大问题。目前，改变管道形状、增加卡箍、施加阻尼器是主要的调节管道的固有频率，减小管道振动的主要方法[5]。李鑫等提出了基于系统特征阻抗，通过优化卡箍布局来进行管路减振，并验证了其有效性［6］；陈艳秋等在有限元的基础上采用遗传算法对发动机导管进行了优化，能够满足快速实现发动机管路的振动设计[7]；Kwong等采用遗传算法对管路卡箍布局进行了优化，并用试验验证了其理论的可靠性[8]。总体而言，这些方法都有显著的减振效果，但是有时需要一定的管道现场外部支撑，这在某些情况下可能难以满足。动力吸振器是一种对安装条件依赖相对较少的被动减振方法，它能有效的解决无法施加卡箍和改变管形等问题，但此方法只有在动力吸振器固有频率和管道工作频率相同时，减振效果才明显。对于不同的管道系统，它们的工作频率是不同的，这样就要针对制造各种与之工作频率对应的动力吸振器，非常繁琐。

本文基于反共振的基本思想，设计出了一种调频动力吸振器，结构简单，安装方便，并且可以进行频率调节，可以满足不同管道系统工作频率下的减振工作。针对实际建了一段简单的三维空间管路，用Ansys Workbench进行了有限元仿真，并且加工出了吸振器，用有限元仿真和实验两方面验证了吸振器的有效性和实用性。

1 调频动力吸振器的基本原理

在实际管路工况中，工作频率段附近的共振点被看做是主要讨论的频率，因此管路系统也可以被简化为单一共振频率下的单自由度模型。调频动力吸振器利用反共振原理，当管路系统发生振动时，同时会带动动力吸振器振动。吸振器的运动产生的惯性力会反作用到管路系统上，从而有效地抑制管路系统的振动。把管道振动系统称为主系统，动力吸振器，也就是新附加的系统称作子系统，组合的系统构成一个二自由度系统[9-11]，如图1所示。

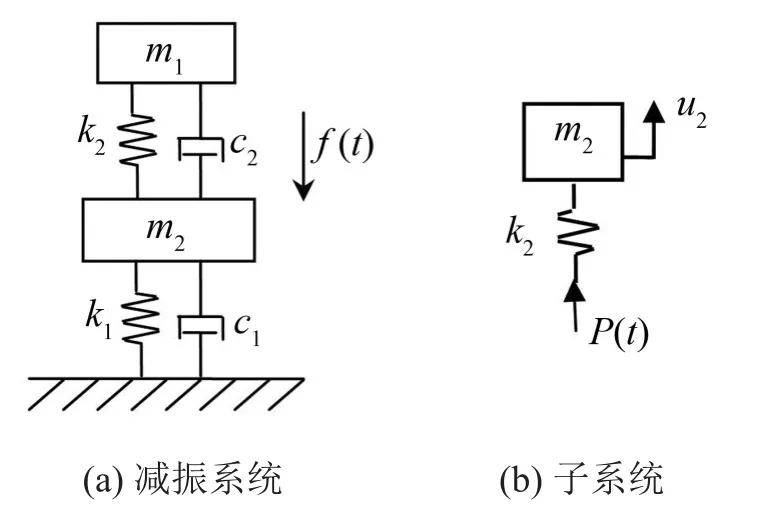
图1 主系统与附加子系统减振

其中的m1，c1，k1分别为主结构的质量、阻尼和弹簧刚度；m2，c2，k2是动力吸振器的质量、阻尼和弹簧刚度。子系统和主系统分离[12]，由动力学原理就可知当外激励频率与子系统的固有频率相等时，质量m1将不振动，吸振器即利用此原理对主系统进行吸振。

2 调频动力吸振器的设计

图2为所设计的调频动力吸振器，其结构上采用螺栓固定，并连接安装在管道上。弹簧片开槽，通过调整质量块在弹簧片上的位置来达到调频的目的。由于调频动力吸振器要在动载荷环境下工作，所以弹簧片采用了弹性较好而且屈服强度较高的弹簧钢65Mn，其厚度在1.5 mm，整体形状是扁平的长方体。内圈夹持件采用了密度较小的合金铝6061；周向则通过4个相互成直角的弹簧片固定4个质量块。质量块由螺栓固定在弹簧片沟槽内，并可在沟槽内移动。整个调频动力吸振器结构包括两个夹持结构、4个弹簧片和与弹簧片数量相等的质量块，以及其他连接螺钉等，主要的基本材料数据见表1。

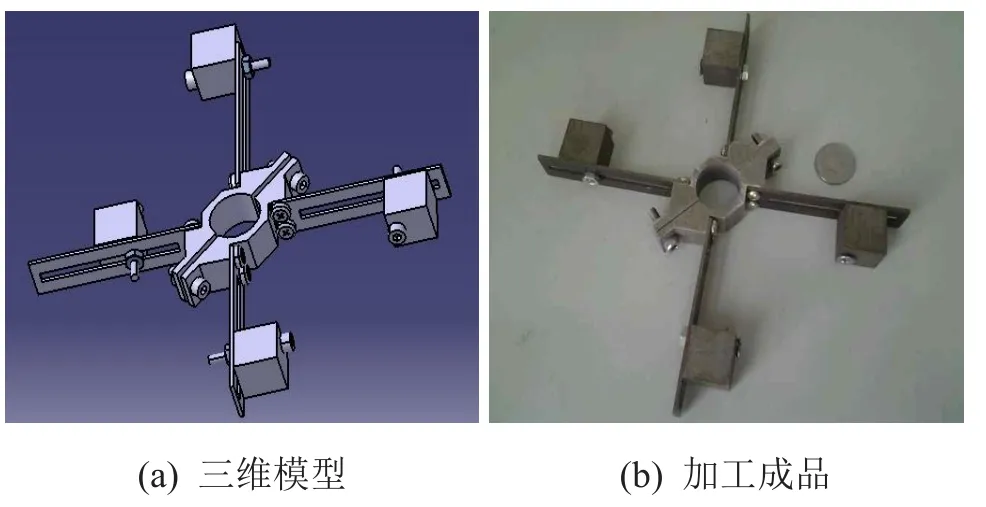
图2 调频动力吸振器

表1 调频动力吸振器各部件材料参数

3 管道振动实验台

为验证调频动力吸振器的吸振效果，本文建立了一个简单的三维空间管道试验台，如图3所示，图中（6）所指分别为X、Z、Y三个方向加速度传感器，分别测取X、Z、Y三个方向的振动加速度，振动台用上海鲁轩仪器设备厂生产的ZD/LX-ATP型号激振器进行管道基础正弦激振。管路系统主结构为空间3个方向上的管路。管路由4根管道通过管接头连接而成，管道所用材料为镀锌钢，外径21 mm，壁厚3 mm，两固定支承间管路总重3.45 kg。卡箍位置在图3中（5）处。

4 管道动力吸振器的有限元仿真验证

4.1 管道有限元模型的验证

为了验证有限元模型的正确性，首先对真实管道系统进行了模态试验。采用锤击法，用力锤分别对图3中管道3个方向进行敲击，如图4(a)、(b)、(c)所示，通过放置在管道上的加速度传感器获取管道系统的频响函数，并得出管道系统的共振频率如表2所示。

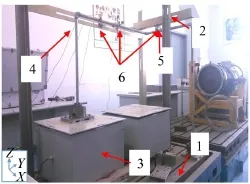
图3 管道实验台

图4 锤击的三个方向

表2 真实管道共振频率结果列表

对管道系统进行有限元仿真，模拟图3所示的实际管道实验台的安装条件，由Catia建模，转化为（.stp）文件导入Ansys Workbench。管路右端的边界条件为固定支撑，左端也就是1处边界条件为固定支撑。卡箍沿管道方向长为30 mm，边界条件设置为弹性支撑。模态分析时卡箍由内径21 mm，外径21.5 mm，长30 mm的圆筒代替。管路模态分析时卡箍具体位置及管路模态分析边界条件如图5所示。对管路进行模态分析，得到其各阶固有频率。

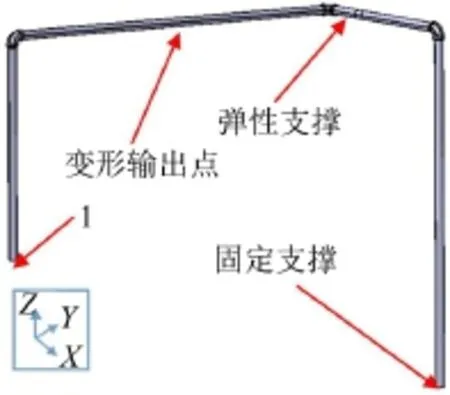
图5 模态分析管路模型

表3为有限元仿真计算得到的模态仿真结果，管路模态分析时，卡箍的弹性模量为6×1012Pa时，结果显示与真实管路模态试验所测得的数据非常接近。由此可认为仿真的管道模型基本符合真实管道模型，增加了仿真的正确性。

表3 仿真管道共振频率结果列表

4.2 基于管道有限元仿真计算的可调频式减振器减振效果验证

对调频动力吸振器进行等效简化，忽略螺丝等部件，得到简化模型利用Ansys Workbench进行模态分析。其边界条件在夹持件内弧设置固定支撑，如图6所示。

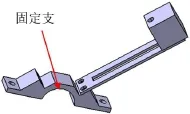
图6 模态分析调频动力吸振器模型

根据动力吸振器吸振原理，可以得知当动力吸振器固有频率和管路固有频率相同时，其达到的减振效果最为理想。通过调节四个质量块在弹簧片上的位置（质量块与内圈夹持件的距离），在Ansys Workbench中对调频动力吸振器进行模态分析，结果显示调频动力吸振器频率调节范围64.943 Hz～362.56 Hz。具体固有频率分析结果如表4所示。

表4 调频动力吸振器模态分析结果列表

通过谐响应分析验证管路系统在75.8 Hz和96.18 Hz两个共振频率下管路系统未夹装调频动力吸振器和夹装调频动力吸振器两种情况下的分析结果，并进行对比验证调频动力吸振器确有调频减振效果。图5中指出了管路振动谐响应分析时的边界条件以及变形输出点，管路系统右端固定支撑，左端（1）处则施加基础激励，激励幅值为1×10-3m。

（1）管系75.8 Hz下的Z方向减振计算

管路系统在75.8 Hz振动频率下未夹装调频动力吸振器的振型表现为Z方向上垂直振动，且在中间位置表现最大振动位移，如图7(a)所示。管路系统在夹装调频动力吸振器后振型如图7(b)所示，可以看出，管路系统振动明显降低。

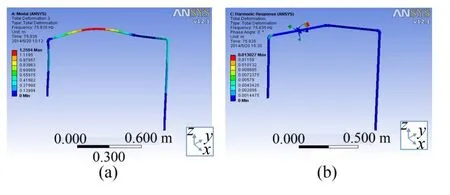
图7 管系振动模态（75.8 Hz）

管路系统谐响应分析频率范围设置在75 Hz～85 Hz，其振动位移幅值如图8所示。谐响应分析结果显示：在75.8 Hz附近未夹装动力吸振器管路系统振动明显强烈，达到7.6×10-3m，而夹装动力吸振器后振动位移明显下降，最低下降至6.86×10-5m。

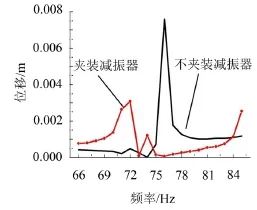
图8 75.8 Hz谐响应分析结果对比

（2）管系96.18 Hz下的X方向减振计算

管路系统在96.18 Hz振动频率下未夹装调频动力吸振器的振型表现为X方向上水平振动，且在中间位置表现最大振动位移，如图9(a)所示。管路系统在夹装调频动力吸振器后振型如图9(b)所示，同样可以看出，管路系统振动明显降低。

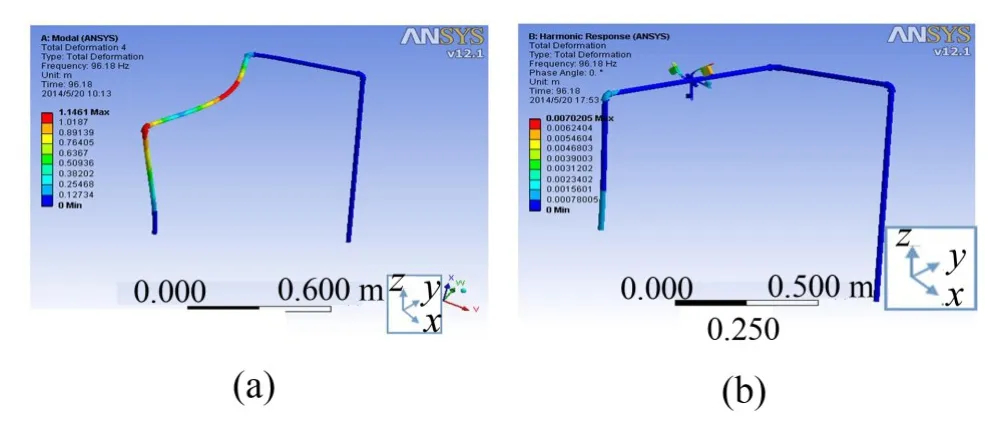
图9 管路振动模态（96.18Hz）

管路系统谐响应分析频率范围设置在90 Hz～110 Hz，振动振型查看设置在96.18 Hz。其振动位移幅值如图10所示。在96 Hz附近未夹装动力吸振器管路系统振动明显强烈，达到5.67×10-2m，而夹装动力吸振器后振动位移明显下降，最低下降至1.24× 10-5m。

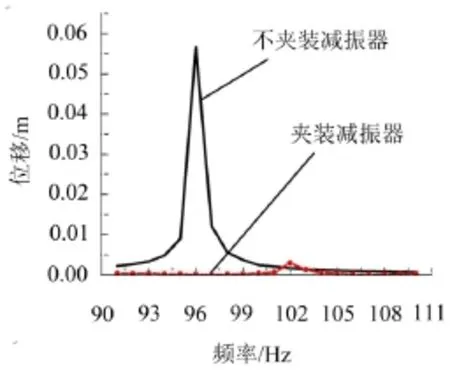
图10 96.18 Hz谐响应分析结果对比

通过对上述2个频率下的仿真分析结果显示，调频动力吸振器对管路系统在76 Hz和96 Hz两处频率点的振动都具有明显减振效果，达到了预期目的。在此过程中，对调频动力吸振器在Catia中对质量块在弹簧片上的位移进行调节。进行谐响应分析的管路系统上夹装的调频动力吸振器质量块在弹簧片上的位移分别为53 mm和43 mm，经过对调频动力吸振器简化模型的模态分析显示，其1阶频率分别为76.5 Hz及96.8 Hz，与所分析的两组管路系统振动频率非常接近。谐响应分析验证调频动力吸振器减振效果与原理相符。

5 空间管系减振实验验证

为进一步验证调频动力吸振器在实际中的减振作用，本节通过加工出的真实调频动力吸振器，在实际管路系统上进行验证实验。为此设计了两套实验方案：分别验证管路系统在76 Hz和101.3 Hz工作频率下减振效果，比较调频动力吸振器在管路系统振动最大点处的质量块在弹簧片不同位置时管路系统减振效果。

5.1 共振频率76 Hz管系调频减振对比分析

图11中显示了质量块在不同位置下的吸振器安装情况，其中，(a)、(b)、(c)、(d)、(e)、(f)中质量块所处位移分别为60 mm、52 mm、45 mm、34 mm、26 mm、14 mm。利用激振器对管道进行76 Hz的基础正弦激振来进行未夹装调频动力吸振器的情况以及6组调频实验，共计7组实验。测得每组实验的管路系统振动加速度幅值，经过对比不难看出，当质量块距离为45 mm时，调频动力吸振器对管路系统减振效果最好，如表5所示。未夹装调频动力吸振器与质量块移动到弹簧片上45 mm位置处的减振效果对比如图12所示。

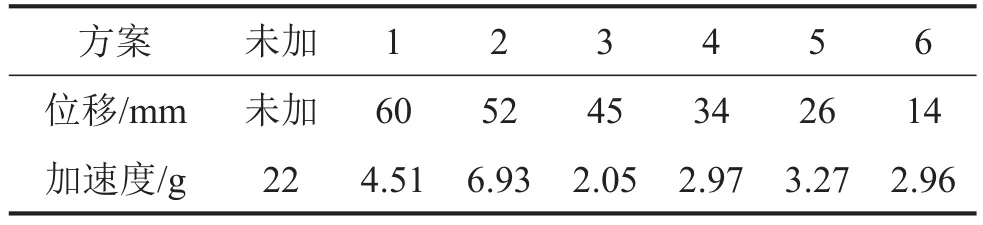
表5 76 Hz管路振动调频对比实验结果

图11 调频动力吸振器的频率调节

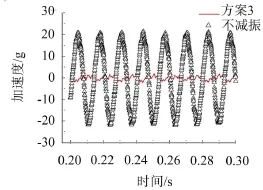
图12 76 Hz最佳减振效果

5.2 共振频率101.3 Hz管系调频减振对比分析

同样进行7组实验，质量块的位置仅仅（c）图的位置（方案3）为43 mm，其他与图11完全相同，同样可以看出，当质量块位移为43 mm时，调频动力吸振器对管路系统减振效果最好。结果如表6所示。未夹装调频动力吸振器与质量块移动到弹簧片上43 mm位置处的减振效果对比如图13所示。

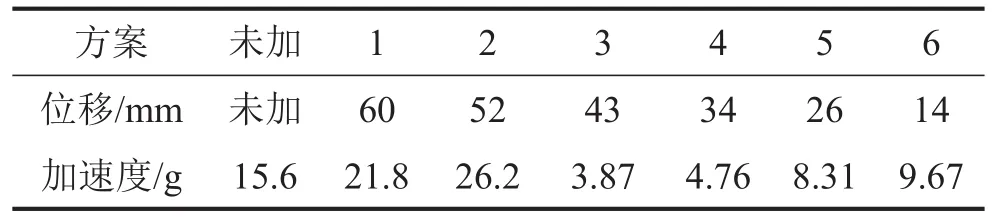
表6 101.3 Hz管路振动调频对比实验结果

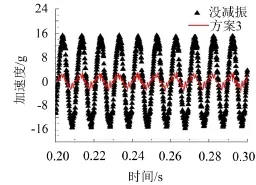
图13 101.3 Hz最佳减振效果

6 结语

（1）调频动力吸振器对管路系统振动减振效果明显，且只要通过改变质量块的位置就能很好的解决管道系统在不同的工作频率下的减振工作；

（2）在进行调频减振试验中，观察表5和表6可以发现调频动力吸振器在管路系统振动调频减振过程中遵循一定规律。质量块在最佳减振位置加大位移，振动会明显增加；而在最佳减振位置减小位移，振动则稍微增强。由此可见调频动力吸振器遵循动力吸振器减振原理，与模拟仿真分析结果得到相互验证。

[1]航空发动机设计手册总编委会.航空发动机设计手册（第19分册）转子动力学及整机振动[M].北京：航空工业出版社，2000：208-226.

[2]陈果，罗云，郑其辉，等.复杂空间载流管道系统流固耦合动力学模型及其验证[J].航空学报，2013，(3)：597-609.

[3]宋港，陈卫东.主动式自调谐吸振器在浮筏隔振系统中的应用[J].噪声与振动控制，2012，(3)：49-54.

[4]孙卫红，晏欣.潜艇振动与噪声控制技术的最新研究进展[J].噪声与振动控制，2012，(5)：6-10.

[5]王全娟，陈家义，李继民.基于功率流方法的多自由度系统吸振控制[J].声学学报，2002，(3)：276-281.

[6]李鑫，王少萍.基于卡箍优化布局的飞机液压管道减振分析[J].振动与冲击，2013，32(1)：14-20.

[7]陈艳秋，朱梓根.基于遗传算法的航空发动机管路优化设计[J].航空动力学报，2002，17(4)：421-425.

[8]Kwong A H M,Edge K A.A method to reduce noise in hydraulic system by optimizing pipe clamp locations[C].Proceedings of the Institution of Mechanical Engineers,Part I [J].Journal of Systems and Control Engineering,1998, 212(14):267-280.

[9]阿舟，姚起杭.振动控制工程[M].北京：航空工业出版社，1989：19-20.

[10]肖红林，何林.阻尼动力吸振器的仿真设计[J].航海工程，2002，5：21-23.

[11]曾胜，任意，程涛涛，等.利用调谐质量阻尼器进行管路系统减振[J].振动、测试与诊断，2012，32(5)：823-826.

[12]胡海岩，孙久厚，陈怀海.机械振动与冲击[M].北京：航空工业出版社，2002.82-87.

Study and Experimental Verification on a Dynamic Vibration Absorber with FrequencyAdjustable

ZHOU Di1,CHEN Guo1,LIU Ming-hua2,LUO Yun2, HOU Min-li2,LIU Bin-Bin1
(1.College of CivilAviation,Nanjing University ofAeronautics andAstronautics, Nanjing 210016,China; 2.ChengduAircraft Industrial(Group)Co.Ltd.,Chengdu 610092,China)

A dynamic vibration absorber with frequency adjustable was designed based on anti-resonant principle.The leaf spring with moveable mass block was installed at the point of the pipeline where the resonant displacement reached the maximum.By moving the mass block on the leaf spring,the vibration reduction of the pipeline could be realized for different frequencies.Then,a spatial pipeline was built.The finite element simulation and the vibration test for the pipeline were carried out.The ability of the designed dynamic vibration absorber for vibration damping of the pipeline which possesses different natural frequencies within the available range of frequency was validated.It is concluded that the best damping effect of the dynamic vibration absorber can be obtained through adjusting the position of mass block on the leaf spring.And the best installation location of the absorber is where the maximum resonant displacement occurs on the pipeline.This work is of important significance for practical application of the dynamic vibration absorbers.

vibration and wave;pipeline;vibration suppression;dynamic vibration absorber;frequency adjustment;finite element analysis

O328

A

10.3969/j.issn.1006-1335.2015.02.048

1006-1355(2015)02-0217-05

2014－09－24

国家自然科学基金资助项目（61179057）；成都飞机工业（集团）有限责任公司项目资助

周笛(1990－)，男，湖南省耒阳市人，硕士研究生，主要研究方向为减振技术研究。

陈果(1972－)，男，博士，南京航空航天大学教授、博士生导师。E-mail:cgzyx@263.net