大型卫星分舱段振动试验技术
江 浩,张 利,程世祥,李太平
(上海卫星装备研究所 第二研究室,上海 200240)
大型卫星分舱段振动试验技术
江 浩,张 利,程世祥,李太平
(上海卫星装备研究所 第二研究室,上海 200240)
研究了大型卫星的分舱段振动试验技术,基于整星和分舱段振动试验时的测试点加速度响应的幅值相对误差累积最小,推导了一种舱段振动试验输入加速度谱的计算方法。以某型号结构星为研究对象,对分舱段输入条件进行了预示,开展了整星和舱段的振动试验研究。试验结果的分析表明,试验结果和理论吻合良好,分舱段和整星振动试验的响应差异主要取决于整星和舱段的频响函数特性。用提出的方法计算的分舱段输入能够保证测试点分舱段振动试验时的响应与整星振动试验时的误差最小。
振动与波;卫星;分舱段;振动试验;响应误差;舱段输入
随着国家安全和经济建设等需求,一大批空间探测项目和军事卫星工程项目将进行立项研究,这些卫星多具有有效载荷体积大、质量重、结构复杂、活动部件多等特点。整星质量大使其对振动台的反共振影响大,尺寸大使其很难保证界面输入振级的均匀性,质心高可能导致较大的正交振动[1]。在某些情况下,质量的增大甚至已经超出了现有振动台的推力范围。在欧美等发达国家,采用多振动台并行激励可以较好地解决该问题,如ESTEC使用8个液压台组成的垂直向2 520 kN、二个水平向各1 260 kN推力的HYDRA系统,4×160 kN与2× 200 kN的电动振动台系统[2-4],美国NASA Glenn研究中心的18台液压作动并推系统[5]。然而,其中涉及的多振动台的同步振动控制等关键技术对我国尚属禁运技术,国内在此方面也没有突破性进展。近年来,大型卫星的设计向着模块化发展,即整星由各种不同功能的通用舱段组合而成。因此,在确保分舱段与整星振动试验结果等效的前提下,对组成卫星的各舱段制定合理的试验条件,以舱段振动试验代替整星振动试验,是一种克服振动台推力不足造成的整星振动试验无法进行的有益尝试。同时,对于模块化设计的卫星而言分舱段振动也可以大大减少试验小相关工作量。本文推导了卫星分舱段振动试验的输入条件求解方法,并设计试验进行了验证,结果表明该方法可以较好地满足卫星分舱段振动试验的需求。
1 分舱段输入的求解
一般而言,卫星振动试验条件都是由运载或总体设计单位针对整星而非舱段给出,分舱段振动试验的关键就是求组成卫星的各舱段在分离状态下单独进行振动试验的输入,使得输出等效于整星振动时的输出,以证明卫星结构经受了同等的考核。如图1所示。在振动学中,求解系统输入属于动载荷识别问题[6],可以在时域求解和频域求解[7-12]。频域求解主要是获得动载荷的谱,时域识别主要研究动载荷的时间历程。

图1 卫星分舱振动试验实施示意图
对于实际的卫星振动试验,输入条件是振动台台面在测试频段内的加速度谱的幅值,因此可在频域求解。对于整星试验和分舱振动试验
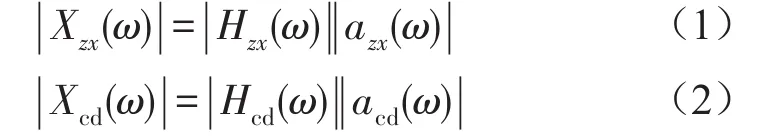
式中X(ω)测试点响应加速度谱向量,a(ω)为振动台输入的加速度谱向量,H(ω)为测试点的频响函数矩阵。下标zx和cd分别表示整星和舱段。
考虑到卫星振动试验为单输入,问题可以简化。在卫星的某一舱段上取m个测试点,这些测试点在整星和舱段振动试验时,输入的加速度谱幅值分别为和的情况下,两次试验之间选定测试点的响应幅值累积相对误差为

将(1)和(2)代入(3)可得

若对结构上的任意测试点i和j满足

式中c为一个常数,即可求得分舱输入
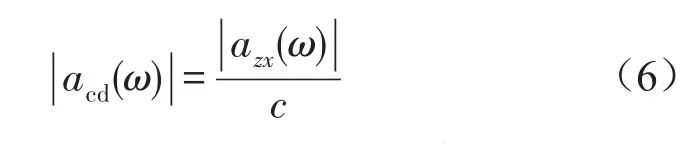
保证测试点在分舱和整星振动试验时加速度响应谱幅值完全相等,但是这一条件通常并不满足。
因此,为了使分舱和整星振动试验获得对卫星近似相同的考核效果,应当使测试点在这两种情况下响应幅值累计误差最小,即求解使(4)式最小的加速度谱幅值 |azx(ω)|。该问题等价于求使得误差的二范数极小,即

将上式展开可得到

由上式可求得分舱振动试验时振动台台面输入加速度谱幅值为
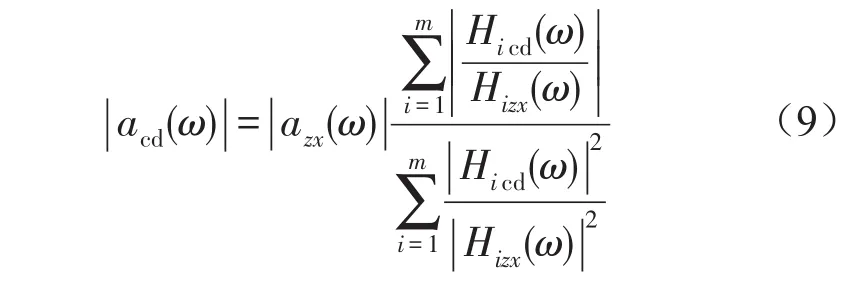
按照上式的输入谱进行分舱振动试验,测试点和整星振动试验时的响应累积相对误差可以达到最小。上式也表明,求得的分舱段输入实际上是整星输入的一种修正,修正系数和舱段/整星的幅频响应的比值有关。
2 振动试验设计
2.1 卫星结构及状态
本次试验的对象为某型号结构星,整星由星体结构舱+变轨舱构成,如图1所示。星体结构舱是本次分舱段振动试验的主要考察对象,与变轨舱结构间采用包带式舱间解锁装置。该舱由舱间连接环、载荷舱、服务舱、星体结构、加强支架、紧固件等部分组成。星体结构舱为模样产品,层板中无预埋热管,舱外的太阳电池阵为配重件,两个天线为结构模拟件,其它单机均为质量质心模拟件。变轨舱结构、内贮箱及推力器组件为模样产品,贮箱内充模拟工质。
2.2 实验设备、控制方法及传感器布置
试验设备包括LING振动台、LMS数采、加速度传感器。正弦振动试验采用工装与产品安装界面的四点平均控制方法,每个控制通道的数据处理方式采用跟踪滤波峰值法,控制点相隔90o均匀分布。控制精度要求为25 Hz以内频率误差不超过0.5 Hz,高于25 Hz频率误差不差过2%;加速度幅值误差不超过10%。
卫星共布设42个振动响应测点,测量振动加速度响应,图2所示为本次试验星体结构舱的加速度传感器布置及编号。

图2 星体结构舱的加速度传感器布置及编号
2.3 振动试验流程
卫星分舱段振动试验包含多组试验:
1)为确定卫星测点的频响函数,进行整星和舱段的小量级正弦扫频预试验;
2)根据运载给出的整星振动实验条件和1)获得的频响函数,按照式(8)计算分舱段试验条件,进行分舱段的满量级振动试验;
3)由于本次试验对象的整星满量级振动试验推力需求在振动台推力范围之内,进行整星满量级振动试验用于和分舱段振动对比。
3 试验结果及讨论
3.1 频响函数特性及舱段输入
由于舱段相对与整星结构的变化,测试点在整星和分舱段振动时三个方向的动力学特性差异较大,其加速度频响差异也较大。同时,卫星结构具有X和Y向的对称性,相应的的幅频响应都具有一定的相似性。一般而言,低频段频响函数反映了结构的整体动力学特征,卫星X和Y向的振动在低频段可近似看作梁的竖直摆动,因此,同一高度处的测试点频响比较接近,反之则相差较大,测试点在Z向振动试验时则无此特征。即测试点在进行X和Y向振动试验时,低频段的幅频响应呈现分层相似的特点,同一层上的4个测试点彼此差异较小,与其它层上测试点差异较大。图3给出的19号—30号测试点在整星和分舱段振动时的加速度幅频响应证实了这一分析。Z向则无分层相似的特点。由于卫星结构X和Y向结构的相似性,后续试验结果也较为接近,因此后续对Y向试验不予讨论。
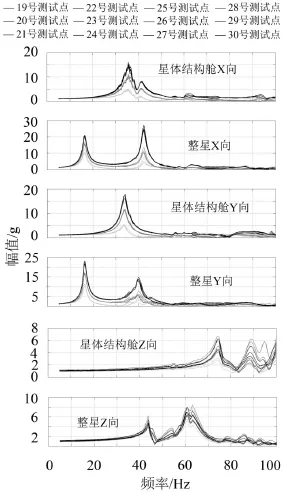
图3 15—30号测点分舱段/整星振动时幅频响应
星体结构舱第二层(23号—26号测点)和第三层(27号—30号测点)重要载荷较多,振动试验主要考核对象也是这两层。由式(5)可知,不同测试点的舱段/整星的幅频响应比越接近,求得的分舱段输入条件就越容易保证测试点分舱段与整星振动输出之间的累积相对误差越小。因此,在计算分舱段振动输入时应尽量选择分舱段/整星幅频响应比近似相等的点。根据分舱和整星X向幅频响应呈现分层相似的特点,它们的比值也应呈现同一特征。图4给出的位于这两层部分测试点X向的分舱段/整星幅频响应比值证实了这一点;Z向则整体上较接近,但在42 Hz~58 Hz呈现奇偶测点彼此相似的特点。这是因为结构在Z向奇数和偶数测试点处的单机模拟件的质量特性,各奇数测点之间和各偶数测点之间较为接近,奇数和偶数相比较则有一定差异。综上,计算星体结构舱振动输入条件时,X向输入条件1和2分别选择了位于第二层的19号—22号测试点和位于第三层的23号—26号测试点;Z向输入条件选择了偶数测试点,这些点称之为等效测试点。可以推断,舱段/整星幅频响应比呈现分层相似的特征,不同的输入条件仅能保证计算该条件时选择的等效点分舱段响应对整星响应的良好逼近,非等效点则无法保证。
观察图4还可发现,各测试点的分舱段/整星幅频响应比在低频段接近程度优于高频段。这是因为低频段的频响函数反映是结构的整体动力学特性,较高频段反映局部动力学特性。结构低频段的整体动力学特性具有一定的相似性,而高频段的局部动力学特性则彼此差异较大。因此在整个测试频段内舱段/整星幅频响应比呈现低频近似高频相异的特点。同样可以推断,等效测试点的分舱段试验响应与整星试验响应的吻合程度必然是在低频段优于高频段。

图4 部分测点分舱段/整星幅频响应比
图5给出了整星和计算的X向星体结构振动试验的满振输入曲线。由图可知,分舱段输入曲线比整星输入复杂,分舱段输入在某些频段内量级超出了整星输入多倍,在另外一些频段内又远小于整星输入。选择不同测试点作为等效计算的输入条件也有差异。按照求得的舱段满振输入进行满量级振动试验,由于测试对象对振动台的反作用,实际控制输入并不严格等于计算的输入。
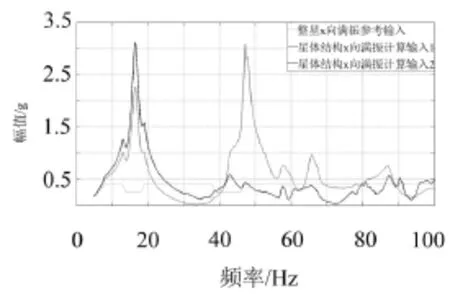
图5 整星和星体结构分舱段X向输入
3.2 测试点响应比较
图6比较了星体结构舱第二层和第三层上部分测试点在整星、分舱输入条件1和分舱输入条件2下进行振动试验获得的加速度响应幅值谱。由图可知,按照等效点计算的输入条件,可以保证等效测试点在分舱试验时具有和整星试验时非常接近的加速度响应幅值,非等效测试点则差异较大。这是因为选择等效测试点在整星和舱段振动试验时频响函数比较为接近,与非等效测试点则有较大的差异,试验结果证实了前面的推断。同样地,由于各等效测试点频响函数比在低频段近似程度优于高频段,其分舱段试验响应与整星试验响应的吻合程度也是在低频段优于高频段。

图6 整星和星体结构分舱段部分测点X向响应比较
Z向分舱段振动试验条件是选取偶数点作为等效点计算得出。图7给出了部分测试点在整星和星体结构分舱段Z向振动时的响应,其中(a)图为偶数测点,(b)图为奇数测点。其中,偶数测点在5 Hz~75 Hz的频段内吻合良好;奇数测点也较为吻合。虽然星体结构分舱段输入是按照偶数测试点等效进行计算,但是由图4可知,奇数测试点的舱段/整星幅频响应比和偶数点也较为接近,可以获得接近的结果。由于在42 Hz~58 Hz频段内奇数点和偶数点的舱段/整星幅频响应比差异较大,因此在42 Hz~58 Hz频段内二者响应差异也较大。由图7同样可知,分舱段和整星响应曲线吻合良好的频段基本在较低的频段,高频段吻合程度变差,其原因与X向一致。

图7 整星和星体结构分舱段部分测点Z向响应比较
4 结语
本文提出了一种基于加速度响应幅值误差最小化原则的卫星分舱段振动输入制定方法,以某型号结构星为研究对象,对分舱段输入条件进行了预示,设计并开展了整星和舱段的振动试验,对试验结果的分析表明:
(1)试验结果和理论吻合良好,按照卫星分舱振动试验输入计算方法方法,在整星和舱段测试点的幅频响应比较接近的情况下,分舱响应可以实现对整星响应的良好逼近,分舱振动可以获得和整星振动近似的考核效果;
(2)结构上各测试点在低频段能够更加容易获得和整星响应接近的分舱段响应,高频段则难以获得和整星响应接近的分舱段响应;
(3)由于不同测试点的舱段/整星和幅频响应不满足式(5),分舱段和整星振动试验的响应总存在误差,舱段/整星幅频响应比的近似程度决定了分舱段对整星响应的近似程度。
[1]柯受全,金恂叔.卫星环境工程和模拟实验(下)[M].北京:中国宇航出版社,1996,2.
[2]魏铭炎.欧洲空间技术研究中心的试验设施[J].环境技术,2001,6:24-27.
[3]Manfred Degner,et al.Vibration tests for dynamic verification and qualification of the PPE/ENVISAT-1 satellite[C]. Proceedings of 3 rd International Symposium on Environmental Testing for Space Programmes,Netherland,Norrdwijk,24-27 June 1997:83-90.
[4]Otto Brunner.The hydra multi-axis vibration test facility at ESTEC[C].Proceedings of 4th international symposium on environmental testing for space programmes,Belgium, Liege,12-14 June 2001:355-360.
[5]Gerald M.Hill,Richard K.Evans.Advanced distributed measurements and data processing at the vibro-acoustic test facility[C].Proceedings of 25 th Aerospace Testing Conference,October,2009:1-18.
[6]张方,秦远田.工程结构动载荷识别方法[M].北京:国防工业出版社,2011,08.
[7]张丽萍,郭立新.基于逆虚拟激励法的车辆动载的识别[J].东北大学学报(自然科学版),2011,32(3):415-418.
[8]原春晖,郎波.奇异值分解在设备振动激励估算中的应用[J].中国舰船研究,2007,2(2):15-18.
[9]张方,秦远田,邓吉宏.复杂分布动载荷识别技术研究[J].振动工程学报,2006,19(1):81-85.
[10]吴邵庆,史治宇.由有限元—Wavelet-Galerkin法识别桥面移动载荷[J].振动工程学报,2006,19(4):494-498.
[11]胡杰,张希农.一种频域载荷识别的优化方法[J].噪声与振动控制,2009,(6):34-36.
[12]胡寅寅,率志君,李玩幽,等.设备载荷识别与激励源特性的研究现状[J].噪声与振动控制,2011,(4):1-5.
Technology of Satellite Segment Vibration Test
JIANG Hao,ZHANG Li,CHENG Shi-xiang,LI Tai-ping
(Shanghai Institute of Satellite Equipment,Shanghai 200240,China)
Vibration test technology of satellite segments was studied.Based on minimizing the accumulative relative errors of the amplitudes of the acceleration response at the testing points between entire satellite vibration test and segment vibration test,the algorithm for solving the input acceleration spectrum for the satellite segment vibration test was derived. Vibration tests were carried out for the entire satellite and its segments with this algorithm.The results show a good coincidence between the tests and the theoretical computation.It is concluded that the response difference between the entire satellite test and the segment test depends on their dynamical characteristics.The presented algorithm can ensure that the segment response is the best approximation of the entirety response of the satellite.
vibration and wave;satellite;segment;vibration test;response error;segment input
V414.1
A
10.3969/j.issn.1006-1335.2015.02.023
1006-1355(2015)02-0096-05
2014-08-04
总装备部“十二五”星箭可靠性增长及产品化推进工程项目,卫星环境试验模拟技术规范研究(项目编号:46)
江浩(1981-),男,安徽芜湖人,博士,主要研究方向:卫星结构动力学、航天器力学试验技术、主被动隔振技术。E-mail:jh613613@aliyun.com

