基于Matlab的动力总成悬置系统解耦优化

薛 华，刘志强，刘 岩,苏 迎

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000；2.华晨汽车工程研究院，沈阳 110000)

基于Matlab的动力总成悬置系统解耦优化

薛 华1，刘志强1，刘 岩2,苏 迎2

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000；2.华晨汽车工程研究院，沈阳 110000)

以某车型怠速运转时方向盘剧烈抖动为背景，测量动力总成和悬置参数，建立了动力总成悬置系统的6自由度数学模型，通过解耦计算，发现各个方向耦合比较严重，需要进行系统优化设计；应用撞击中心理论，对前后悬置位置进行调整，然后以悬置系统的刚度、悬置倾斜角度为约束变量，使用Matlab的多目标优化函数fgoalattain，以6个方向的耦合最小为目标函数进行优化设计，结果表明此方法能够在一定的约束范围内较好的实现各个方向的解耦，具有较高的实用价值。

振动与波；动力总成；悬置系统；怠速振动；多目标优化；能量解耦

1 悬置

1.1 悬置作用

悬置具有两方面的要求，一是隔离动力总成的振动向车身的传递；二是隔离路面的振动给发动机造成的影响。从舒适性的角度往往希望悬置越软越好，使振动传递率最小，从整车紧凑型来说，由于受发动机舱空间的现在，往往需要较大的刚度，减小振动的位移，这就涉及悬置的三个作用：

支撑作用：将动力总成支撑在车身或者车架上；

限位作用：避免动力总成和其他装置产生干涉；

隔振作用：隔离发动机振动向车身的传递，减小路面激励向发动机的传递。

在发动机横置、前置前驱的动力总成布置形式中，一般采用三点或者四点支撑，左悬置通常与变速箱连接，在隔离激振的同时起到动力总成限位的作用。右悬置与发动机相连，隔离发动机燃烧激励、惯性力激励。前、后悬置通常与变速箱连接布置，承受扭矩，重点起到动力总成的纵向限位。

1.2 设计要求

经客户反映，某车型在怠速运转情况下方向盘抖动强烈，初步分析是由于产生共振引起。

图1 单自由度振动曲线

由隔振理论可知，理想的悬置设计应该是，在低频区，高刚度、大阻尼，在高频区，低刚度、小阻尼[3]。

发动机惯性激振频率计算公式：f=Q·n/60 Q-比例系数，Q=2

此发动机怠速运转转速800 r/min，带入公式得f=26.7 Hz

路面激励为2.5 Hz以内，为了避免路面激励与其他系统产生共振，应使频率至少大于2 Hz[4]，取最小频率为5 Hz[5]。

2 数学模型的建立及参数获取

2.1 建立数学模型

图2中o-xyz为动力总成坐标系，o为动力总成质心位置，x由质心位置指向发动机前段，z垂直指向气缸盖，y由右手定则确定，动力总成具有6个自由度，分别为三个方向的移动和绕三个方向的转动自由度。悬置简化为互相垂直的线性弹簧粘性阻尼元件，为分别与(x,y,z)轴平行的坐标系，动力总成采用横置前置前驱的布置方式[6]。

图2 动力总成悬置系统模型

2.2 初始参数获取

通过称得动力总成质量（kg）和用三线摆测得惯性参数（kg·m2）值，如表1。

表1 动力总成的质量和惯性参数

测得动力总成的质心位置相对测量坐标系的位置为（-16.34，49.97，50.42），各个悬置相对质心位置参数，如表2。

表2 悬置初始位置/mm

通过体积压缩试验测得橡胶参数，如表3。

表3 初始刚度值/(N/mm)

测得悬置安装的初始角度值，如表4。

表4 初始角度值/(°)

3 解耦计算

经过在动力总成坐标系下的解耦计算得各个方向的频率和解耦率，如表5所示。

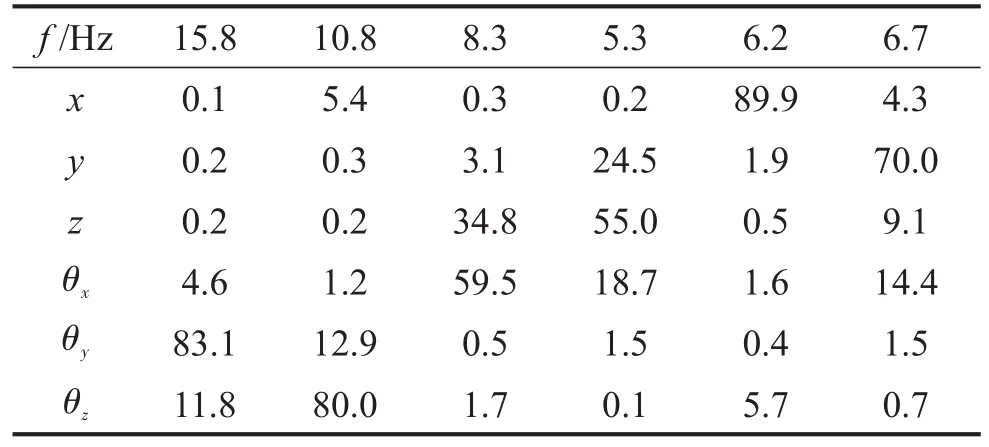
表5 初始频率和解耦率/(%)

从表5中看出动力总成在z、θx、θy方向的耦合比较严重，而且频率之间间隔较小，容易产生运动耦合，容易与其他部件之间产生振动耦合，引起整车的振动和噪声，因此需要进行优化设计。

4 优化设计

4.1 能量解耦法

为了避免与其他附属设备产生共振，同时降低动力总成的振动向车身的传递，也就是振动的传递率，需进行优化设计。传递率与质量、刚度和阻尼有关，由于对于一个现成的动力总成来说，质量是确定性因素，因此需要从刚度和阻尼开展分析，由于阻尼只影响位移，对振动的传递率和频率没有影响，暂不考虑[7]。

对于发动机横置前置前驱的动力总成系统，普遍采用能量解耦法进行解耦和优化，通过对悬置刚度、位置和倾斜角度为变量进行优化，得到在怠速工况下，动力总成的频率合理分布和的解耦率。根据振动理论，动力总成质心运动的数学表达式为

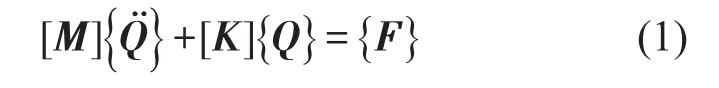
推导得到

[M]，[K]分别是质量矩阵和刚度矩阵，{φ}为模态矩阵，根据质量矩阵和刚度矩阵可求得固有频率和振型。当动力总成以第i阶固有频率和振型振动时，第i个坐标上的能量解耦率[7，11]为

4.2 Matlab多目标优化函数

使用Matlab的多目标优化函数，对各个自由度进行解耦优化，归结为求的最小值，使得

满足约束条件

其中x，weight，goal，b，beq，lb和ub是向量，A和Aeq是矩阵；c(x)，ceq(x)和F(x)是向量函数，他们可以使非线性函数。F(x)是所考虑的目标函数，goal是欲达到的目标值，多目标规划的Matlab函数fgoalattain的用法为

其中 fun是用M文件定义的目标向量函数，x0是初值，weight是权重。A，b定义不等式约束A·x≤0，Aeq，beq定义等式约束Aeq·x=beq，nonlcon是用M文件定义的非线性约束c(x)≤0，ceq(x)=0。返回值 fval是目标向量函数的值。

wi为第i阶固有频率的加权因子。悬置上下限约束条件

非线性约束条件

4.3 优化计算

由撞击中心理论可知，当其中一个位置悬置受到激励时，另一个悬置不产生运动，可以减少振动向车身的传递

Jx—动力总成绕x轴的转动惯量

m—动力总成的质量

L前—前悬置到动力总成质心的距离

L后—后悬置到动力总成质心的距离

根据撞击中心理论,原前后悬置不符合要求，保持后悬置位置不变，调整前悬置的y向的水平距离为170.072，再以悬置刚度（表6）和倾角（表7）为约束条件，设置目标值和各个方向的权重系数为goal=[0.01,0.01,0.01,0.01,0.01,0.01]、weight=[0.01,0.01,0.01，0.01，0.01，0.01]进行优化。得到动力总成在各个方向的刚度，倾斜角度和解耦率[7]。

表6 悬置刚度约束范围/(N/mm)

表7 悬置倾角约束范围/(°)

优化后的刚度值，如表8。

倾斜角度，如表9。

表9 优化后悬置倾角/(°)

固有频率和解耦率(%)，如表10。

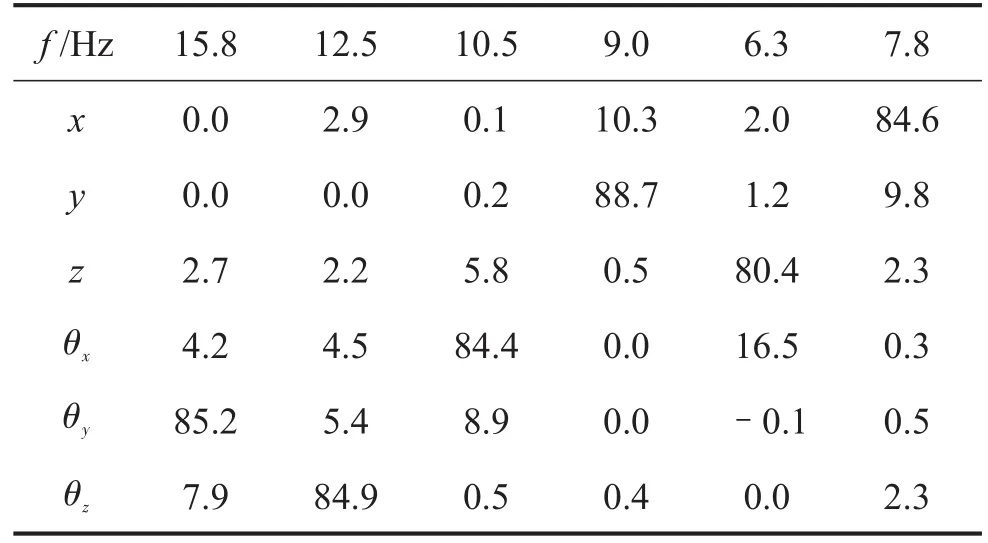
表10 优化后频率和解耦率/(%)

5 结语

从优化结果可以看出，频率分布比较均匀，且都大于5 Hz，避免与路面激励产生共振，各个固有频率的分布相隔大于1 Hz，更好的避免在设计中与其他系统产生干涉，提高系统的可靠性。解耦率的分布保证了在某一方向上占优，并且各个方向上的解耦率都大于80%，避免各个方向振动的相互耦合，提高了整车的舒适性。经过实车验证，发现在怠速运转情况下，方向盘抖动消失，验证了优化结果具有可行性，具有一定的工程应用价值。

[1]时培成，李文江，丁芳.基于振动传递率和能量解耦率的悬置系统优化[J].汽车工程，2009，26(2)：1057-1060.

[2]庞剑，谌刚，何华.汽车噪声与振动理论与应用[M].北京：北京理工大学出版社，2006.

[3]黄鼎友，吉向东.动力总成悬置系统建模及振动仿真[J].江苏大学学报，2005，26（3）：222-223.

[4]陈达亮.动力总成悬置系统怠速隔振优化策略研究[J].噪声与振动控制，2011（05）：54-55.

[5]吕振华，梁伟，上官文斌.汽车发动机液阻悬置动特性仿真与实验分析[J].汽车工程2002（24）：105-106.

[6]李楠.动力总成悬置系统优化与仿真分析[J].重庆交通大学学报，2012，31(1)：125-127.

[7]李玉桂.动力总成悬置系统的布置设计与解耦优化[J].机电技术，2012(1)：49-51.

[8]李涛，贺勇军，刘志俭.等编著.Matlab工具箱应用指南—应用数学篇[M].北京：电子工业出版社，2000.

[9]陈荫三，余强译.汽车动力学[M].北京：清华大学出版社，2009.

[10]饶著，李欣业，张明路译.机械振动[M].北京：清华大学出版社，2009.

[11]沈志宏，郭福祥，基于能量解耦法的动力总成悬置系统优化设计[J].噪声与振动控制，2010（03）：35-37.

[12]梁天也，史文库.发动机悬置研究综述[J].噪声与振动控制，2007（01）：6-9.

Decoupling and Optimal Design of a Powertrain Mount System Based on Matlab

XUE Hua1,LIU Zhi-qiang1,LIU Yan2,SU Ying2
(1.College of Mechanical Engineering,Liaoning Technical University,Fuxin 123000,Liaoning China; 2.BrillianceAuto Engineering Research Institute,Shenyang 110000,China)

It is known that powertrain mount system plays an important role in vehicle design.For the steering wheel of a car shaking violently in the idle condition,its powertrain and suspension parameters were measured,and a 6-DOF mathematical model of the powertrain mount system was established.The decoupling analysis showed that the coupling effect was serious in all the directions.Therefore,system optimal design was done.Firstly,the mount position was adjusted based on the impact center theory.Then,choosing the rigidity of the mount system and the mount inclination angle as the constraint variables and the minimum decoupling of the 6 directions as the objective function,the optimal design was done using the multi-objective optimization function“fgoalattain”of the Matlab.The results show that this method can realize better decoupling in all directions within a certain range of constraints and has high practical application values.

vibration and wave;powertrain;mounting system;idle vibration;multi-objective optimization;energy decoupling

U461.4

A

10.3969/j.issn.1006-1335.2015.02.016

1006-1355(2015)02-0065-04

2014－08－06

薛华（1960－），男，副教授，硕士生导师，研究方向：工矿车辆的可靠性与故障诊断。E-mail:xuehua601229@126.com

刘志强（1986－），男，内蒙古呼和浩特人，硕士生，主要研究方向：动力总成及整车振动控制研究。

发动机作为整车的动力装置，对于整车的振动和声学性能的影响具有重要的作用，也就是通常所说的NVH特性。随着技术进步以及道路条件的改善，作为车辆动力装置的发动机成为主要噪声源。NVH性能的优劣，直接决定了整车在市场当中的占有率。在最近的几十年中，消费者对汽车的舒适性提出了更高的要求，作为汽车的生产厂家，为了提高市场的认可度，在满足法规和成本要求的前提下，都在尽可能生产出市场认可的产品。目前在高端车市场上较多的采用了主动悬置和半主动悬置来提高整车使用性能，作为在传统车型中较多使用的橡胶悬置，由于其较高的可靠性和低成本，一直备受汽车厂家的青睐[1，2，12]。