基于AR功率谱的高速列车转向架故障信号分析

段旺旺，金炜东

（西南交通大学 电气工程学院，成都 610031）

基于AR功率谱的高速列车转向架故障信号分析

段旺旺，金炜东

（西南交通大学 电气工程学院，成都 610031）

高速列车转向架是否故障及故障种类对列车运行的安全性有重要的影响。为了及时高效的对转向架关键部件进行故障诊断，本文选用高速列车转向架典型故障振动信号，提出了运用功率谱与主成分分析相结合的方法提取信号特征，先对样本数据进行功率谱估计，构造包含所有工况的特征频点数组，将这些频率点在每个样本的功率谱中对应的幅值作为特征向量，再通过主成分分析降维处理，去除冗余的特征项，最后经过支持向量机分类判断出故障种类。用加速度和位移传感器选取5个测点，取得了满意的识别结果，准确率在90%以上，验证了该方法的有效性。

振动与波；故障诊断；高速列车；信号分析；转向架

随着我国高速铁路的快速发展，列车的速度不断提高，长期服役的安全性态会发生变化，若隐藏的故障不能及时排除，将对列车的安全行驶造成极大的威胁。如何在高速列车的振动数据中有效提取异常特征，并快速准确的估计出高速列车所处的状态，判断出列车转向架的故障种类，对高速列车的行车安全具有重要意义。目前针对列车振动信号的分析方法主要有经验模态分解[1]、小波分析[2]和分数阶傅里叶变换[3]等，求取的特征向量大都缺乏物理意义，而且计算量大，实时性较差。

功率谱反映了随机信号各频率成份功率能量的分布情况，可以揭示信号中隐含的周期性等有用信息，对于机械设备各种特征频率的确定是对设备进行故障诊断的基础，当机械设备发生故障时，均在某些特征频率附近出现明显的峰值，功率谱通过反映各频率成分能量的分布关系，更容易得到峰值出现位置处所对应的频率[4]。

本文通过运用现代功率谱估计提取具有物理意义的特征向量，再通过主成分分析对特征向量进行降维优化，去除了冗余的特征对分类的干扰，提高了分类的准确率，也提高了程序运行效率，真正做到快速准确估计出列车的故障种类。

1 高速列车故障种类诊断

列车在高速行驶中产生的振动信号是由多个振动源一起产生的，如发动机、齿轮间隙以及轮轨关系导致的车体其他部件的非周期振动，当然还有对应于不同车况的一些具有稳定频率的周期性振动。由于功率谱能突出周期性振动信号，周期振动在功率谱中对应尖锋，而背景与宽锋对应各类噪声，所以列车在不同的工况下得到的功率谱的谱峰，有属于公共信号造成的，也有属于每种工况具有特征频率的振动，即便是公共信号在不同工况的影响下因表现的剧烈程度不同；造成谱峰幅值也不同。谱峰对应的频率点就是每种故障的特征频点。由于不同的传感器位置不一样，依托车体的部位不同或部件不同，以及检测方向也不尽相同，决定了不同的传感器检测到的是整个振动车体的局部信息，所以在同一种工况下，不同的传感器检测到的振动信号是有差别的，同时，列车在不同速度下车体的振动情况是有差异的，导致同一个传感器在不同速度下检测到的信号也是不一样的，这就造成了某一工况的特征频点会随列车的速度以及传感器的不同而不同。列车在行驶中转向架主要有以下几种典型工况[5]：正常、空簧失气、抗蛇行减震器失效、横向减震器失效三种单故障，以及横向减震器失效+抗蛇行减震器失效、空簧失气+横向减震器失效、空簧失气+抗蛇行减震器失效三种混合工况，本文将正常工况作为一种单故障，将三种混合故障与之前的四种单故障组成七种故障。

图1为列车振动信号处理流程图，对某一速度某一传感器测到的数据，首先根据先验的信息获得每种工况的特征频点，组成七种工况的特征频点库，对待测信号取特征频点处功率谱的幅值，组成N维特征向量，再对该特征向量进行降维处理[6]，最后通过支持向量机学习分类，估计出转向架故障种类。

2 AR模型功率谱估计

功率谱估计是随机信号处理的重要内容，主要有经典谱估计和现代谱估计，现代功率谱估计较经典谱估计频率分辨率高，应用更加广泛。功率谱能较好的突出混合信号中的周期成分，周期振动在功率谱中对应尖锋，而背景与宽锋对应各类噪声，谱的幅值则反映了振动的剧烈程度。

在现代谱估计中，常用模型有自回归（AR）模型，滑动平均（MA）模型，自回归滑动平均（ARMA）模型，根据Kolmogorov-Szego定理，只要AR模型的阶数p取到足够大，就可以代替ARMA或MA模型。在实际应用中，因为AR模型参数计算相对简单，同时有较高的分辨率，因此被研究的最多。AR模型是一个全极点模型，该模型的输出是当前输入和过去输出的加权和，可有下面的差分公式表示[7]

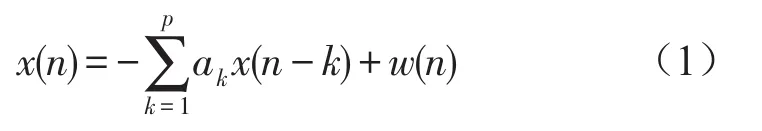
其中p是AR模型的阶数，{ak}为AR模型的参数，w(n)为均值为零、方差为σ2的平稳白噪声序列。将它进行Z变换可得到系统转移函数为

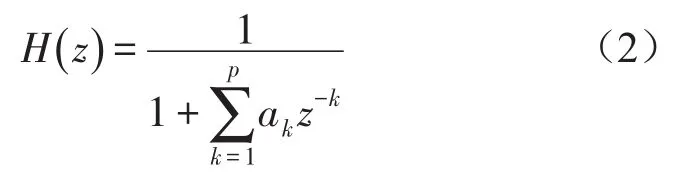
因此{x(n)}的功率谱密度可表示为

只要求得参数{ak}和σ2就能得到功率谱值。

目前主要有三种求取该参数的方法：Levinson-Durbin算法、Burg算法和Marple算法，本文中采用较为通用的Burg算法来估计信号的模型参数，它的基本思想是利用线性预测器对数据向前和向后进行预测，根据总均方误差之和最小的原则来估计发射系数，然后在通过Levinson-Durbin算法递推出AR模型的优化参数[8]。

在AR谱估计中，模型阶次p的选择是一个关键问题，阶次选择过低将会导致功率谱曲线过于平滑，频率分辨率低；而阶次选择过高，又会产生虚假谱峰，干扰正常的谱峰。一般阶次选择有两个准则，最终预测误差准则（FPE）和最小信息准则（AIC），一般对于个数为N的样本，当p/N＜0.1时可视为大样本，对于大样本FPE与AIC效果几乎相同，本文采用AIC准则[9]

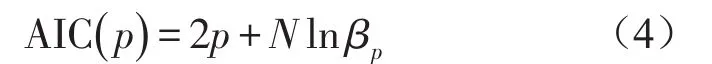
其中N为被测数据个数，βp为p阶AR模型预测误差的方差，一般使AIC(p)的值取得最小值的p值为最佳阶次。

3 主成分分析

主成分分析（PCA)是将多个变量通过线性变换有效的从多维数据中选出能够表示全局的主要数据（主成分），去除噪音和冗余，实现对原来复杂的数据降维。设Xm×n为原始数据，m为样本个数，n为特征维数，其中m＞n，PCA处理的步骤为[10,11]

（1）计算原变量的协方差矩阵Sn×n

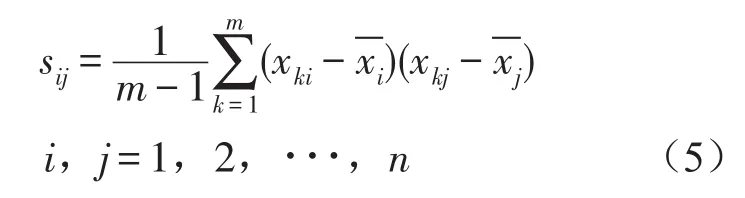
式中xki,xkj分别为原始数据Xm×n中第k行中第i列和第j列的元素，分别为第i列和第j列的数学期望，sij为所求协方差矩阵Sn×n中的元素。

（2）求出Sn×n的特征值λi及相应的正交化的特征向量ai，由大到小取前q个特征值对应的特征向量，就是前q个主成分，选择几个主成分通过特征值贡献率来确定，贡献率表示为

一般，当贡献率大于90%时，就可认为主成分可以反映原变量的信息了。

（3）经上步确定了主成分个数q的值，得到了特征向量An×q，降维后的数据变为

至此，n维数据降到了q维。

4 仿真实验

本文实验数据来自西南交通大学牵引动力国家重点实验室,通过动力学仿真分析的获得[12]。数据为某型号动车组中动车转向架振动故障仿真数据，记录了列车各关键部位的振动信号，包括车体、构架、轴箱上各个部位横向、纵向和垂向三个方向振动加速度和车体、构架、轮对、一系、二系各部位三个方向的振动位移，共计58个通道。不同的通道代表不同位置的传感器。对数据首先进行预处理，因为故障信号都集中在20 Hz以下，所以首先用巴特沃斯滤波器对信号进行低通滤波，去除高次噪声。下图是一组正常工况下车体中部横向加速度传感器在速度200 km/h下的采样数据，分别在滤波前和滤波后的时域和频域波形。

4.1 基于AR功率谱对振动信号特征的提取

对传感器采集到的数据以4 s为单位选取40个样本，下面随机选取200 km/h时车体中部横向加速度传感器采集到的每种工况各一个样本，对其求功率谱。

图2 采样数据滤波结果

由功率谱可以看出，列车每种工况主要的谱峰对应的频点是不同的。对同一种工况，求取部分样本的功率谱，基于统计原则，找出出现频率较高的谱峰对应的频率点，考虑到每个样本对某一主要频点的定位会有较小的偏差，导致不会精确在一个点上，对于这种聚集性的频点；通过筛选选出具有代表性的一个点。现在对每种工况最多取4个公共谱峰对应的频点作为特征频点，正常工况的频点（单位：Hz，以下同)是：1.186、3.797、7.356、11.153。空簧失气的频点是：0.949、4.034、7.594、15.425。抗蛇行减震器失效的频点是：2.136、7.831、11.628、15.425。横向减震器失效的频点是：1.661、4.983、8.543、11.865。横向减震器失效+抗蛇行减震器失效的频点是：1.187、7.831、11.39、14.95。空簧失气+横向减震器失效的频点是：1.661、2.61、3.085、15.188。空簧失气+抗蛇行减震器失效的频点是：2.373、7.594、11.39、15.425。通过对比发现有的频点会出现在不同的工况中，如频点15.425在空簧失气、抗蛇行减震器失效和空簧失气+抗蛇行减震器失效三种工况中都有出现，去掉重复的频点，我们就得到了这组数据中具有代表性的频点组合，和对每种工况取这组频点对应的功率值。由于数值的变化范围很大不便于比较；所以压缩数据范围，对所得功率谱值取对数。对于这组数据，若只考虑区分四种单故障可得到15维特征向量，考虑多故障则可得到21维的特征向量。之前提到传感器的位置不同或车体速度不同，对于同一工况得到的主频率点会有差别，如还是在车体中部横向的加速度传感器，速度变为80 km/h时，正常工况的主频点变为3.085、4.509、13.526、18.035。速度为200 km/h不变时，选择车体后部横向方向的加速度传感器，则正常工况的主频点为1.424、5.458、8.78、12.102。这导致不同的传感器以及在不同速度下采集到的特征维数是不确定的，特征向量是动态变化的。

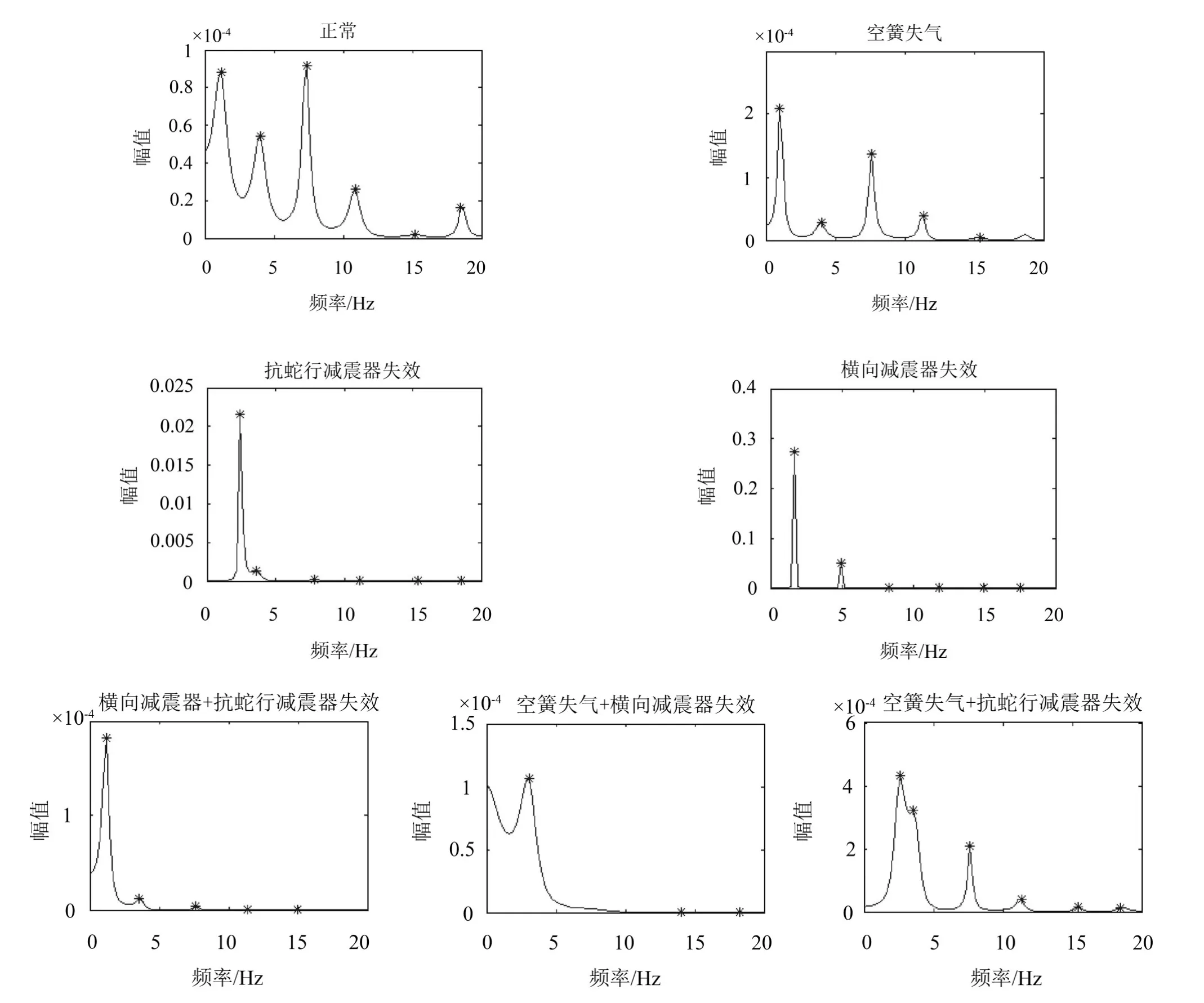
图3 七种工况功率谱图

4.2 PCA对特征向量降维及分类器设计

对于高铁数据，仍然对200 km/h时，车体中部横向加速度传感器采集到的数据进行分析，将对四种单故障进行分类的15维特征经过PCA处理，若取累计贡献率为98%，则特征降到9维，同样对用于七种故障分类的21维特征进行PCA处理，特征也降到了9维，如图4所示，去除了冗余的特征，避免了多余特征的干扰。

图4 PCA贡献率

为了验证本文对故障信号所提特征的有效性，采用支持向量机（SVM）对特征数据进行分类识别。SVM是基于统计学习的VC维理论和结构风险最小化原则的学习机器，它在高维、小样本、非线性数据空间下，具有很好的泛化能力[13]。基于上述数据的对于四种故障分类的实验SVM输入为9维特征向量，对应于运用AR功率谱及PCA对振动信号提取的特征向量，输出为故障种类及分类准确率。实验中，每种工况有40个样本，对4种工况分类有160个样本，对7种工况分类有280个样本，随机选取

其中50%的样本作为训练样本，剩余50%作为测试样本。

对上述特征向量进行SVM分类，整体分类准确率达到了100%。

由于平面作图的限制，现只取前三维特征，作出分类效果图，从图5中可看出四种单故障已经可以很好的分开了。

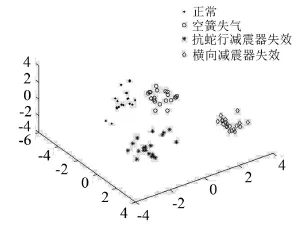
图5 四种故障分类效果图

将对七种故障同样经SVM分类，整体分类准确率达到96.43%。

同样取前三维特征向量作分类效果图如图6所示，除抗蛇行减震器失效和空簧失气+抗蛇行减震器失效两种工况分离效果较差外，其他五种工况已经很好地分开了。

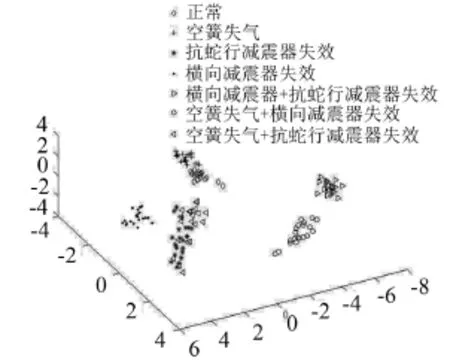
图6 七种故障分类效果图

4.3 仿真结果

下面统计了列车在120 km/h、160 km/h和200km/h时部分传感器对列车七种工况的分类结果。采用加速度传感器和位移传感器，选取五个不同测点，即

(1)是车体中部横向加速度传感器；

(2)是车体后部横向加速度传感器；

(3)是车体前部横向位移传感器；

(4)是车体中部横向位移传感器；

(5)是车体后部横向位移传感器。表1—表3中记录了特征向量经过PCA处理之前的维数以及处理后的维数，最后给出了每个传感器的分类准确率。

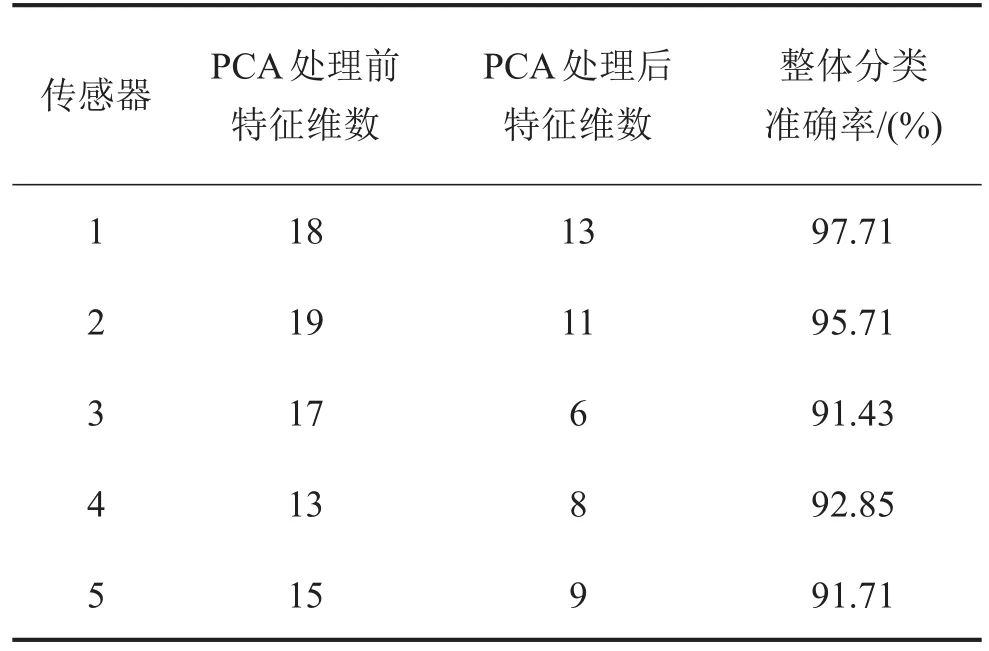
表1 速度是120 km/h时的分类结果

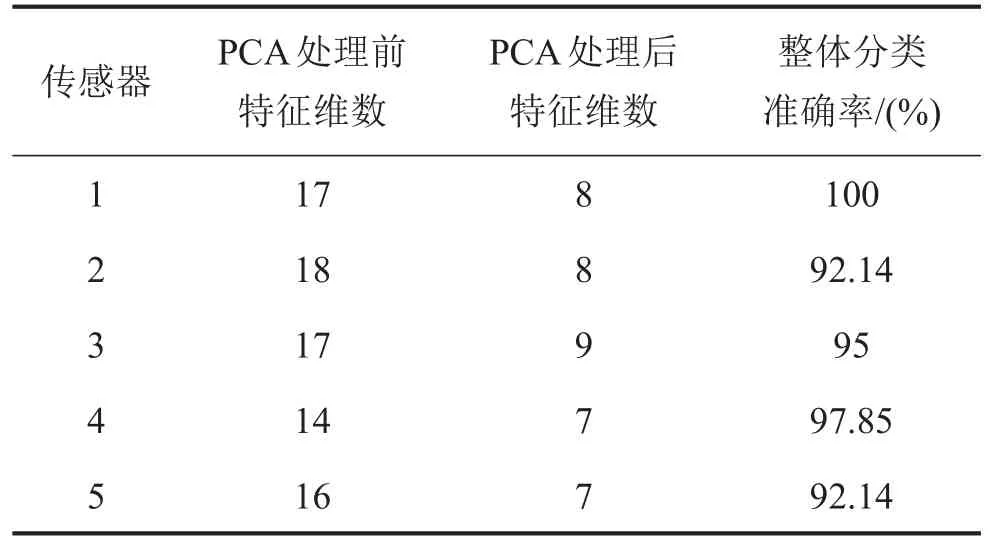
表2 速度是160 km/h时的分类结果

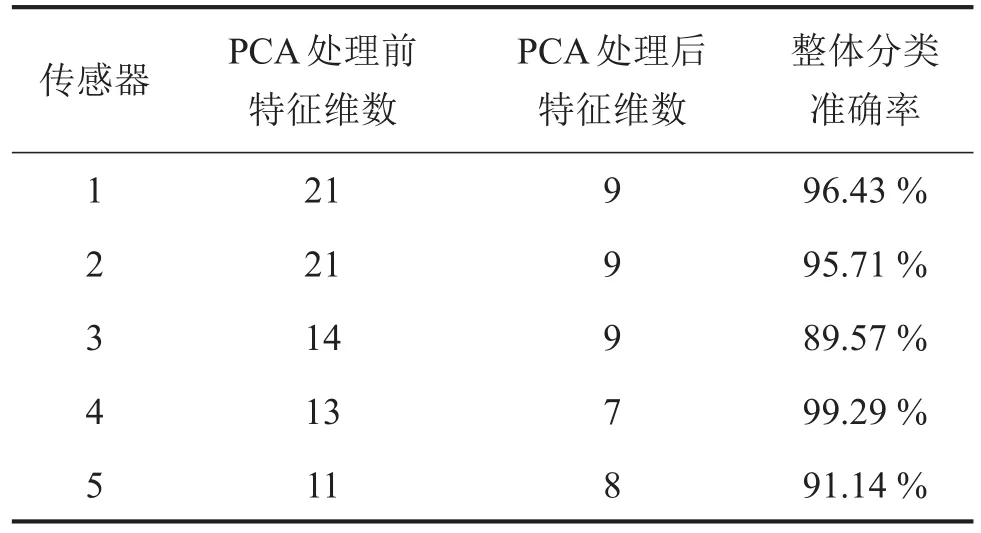
表3 速度是200 km/h时的分类结果

通过上面三个表格可以看出，整体分类准确率基本都在90%以上，有的更高达100%，分类结果是比较好的。通过对多个传感器的决策融合，故障诊断准确率会进一步提高。

5结语

高速列车在行驶中产生的振动信号是由多个振动源共同产生的，是多个具有特征频率的信号和几个其他频率的噪声信号的混合。由于不同故障对车体造成的影不同，导致所含特征信号的频率和幅值有所不同，表现在功率谱上就是不同故障信号的功率谱谱峰位置和幅值不同。统计每种故障的多个样本功率谱的谱峰位置，得到能代表该故障的几个主要频率点，将求得的每种故障的主要频率点组成一个向量，将这频率点对应的幅值在每个样本功率谱中对应的幅值作为特征向量，再通过主成分分析降维处理，去除冗余的特征项，最后经过支持向量机分类，得到了满意的识别结果，验证了该方法的可行性。

[1]秦娜，金炜东，黄进.基于EEMD样本熵的高速列车转向架故障特征提取[J].西南交通大学学报,2014,49(1)：27-32.

[2]刘林艳.基于小波分析的高速列车安全性态评估数据特征分析[D].成都：西南交通大学，2013.

[3]石晶晶.基于FRFT的高速列车安全性态评估数据特征分析[D].成都：西南交通大学，2013.

[4]王金福，李福才.机械故障诊断的信号处理方法:频域分析[J].噪声与振动控制，2013，33(1)：173-180.

[5]黄丽湘，张卫华.机车车辆整车滚动振动试验台设计[J].

铁道车辆，2007，45(1)：5-9．

[6]梁胜杰，张志华，崔立林.基于PCA方法的机械噪声数据处理[J].噪声与振动控制，2010，30(3)：118-122.

[7]张贤达.现代信号处理（第二版）[M].北京：清华大学出版社，2002．

[8]罗丰，段沛沛，吴顺君.基于Burg算法的短序列谱估计研究[J].西安电子科技大学学报(自然科学版)，2005，32 (5)：724-728.

[9]曹兰兰，许小可，索继东.AR模型仿真相关高斯序列的阶数选择[J].火力指挥与控制，2009，34(4)：142-149.

[10]Jolliffe I.Principal component analysis[M].New York: Springer-Verlag,1986:10-28.

[11]范雪莉，冯海泓，原猛.基于互信息的主成分分析特征选择算法[J].控制与决策，2013，(26)：915-919.

[12]张卫华.机车车辆运行动态模拟研究[M].成都：西南交通大学出版社，2006.

[13]任宇飞.SVM模型改进的若干研究[D].南京：南京邮电大学，2013.

Bogie Fault SignalAnalysis of High-speed Trains Based onAR Power Spectrum

DUAN Wang-wang,JIN Wei-dong
(School of Electrical Engineering,Southwest Jiaotong University,Chengdu 610031,China)

The bogie faults and fault types of high-speed trains have an important impact on the safety of train operation.In order to diagnose the bogie fault efficiently,a novel method for feature extraction was proposed by combination of power spectrum with principal component analysis.First of all,the power spectrum evaluation was done using the sample data of the typical fault signals of the bogie,and an array including feature frequency points of a variety of faults was constructed.Then,the power spectrum amplitudes of these points were used to constitute a feature vector,and the redundant features were removed by principal component analysis.Finally,the fault type was identified by SVM.As an example,5 different test points were selected for the testing and satisfactory recognition results were obtained.The correct recognition rate was up to 90%,which verified the effectiveness of this method.

vibration and wave;fault diagnosis;high speed trains;signal analysis;bogie

TP206+.3；TN911.6

A

10.3969/j.issn.1006-1335.2015.01.013

1006-1355(2015)01-0051-06

2014－07－16

国家自然科学基金重点项目(61134002)

段旺旺（1989－），男，西南交通大学电气学院，硕士研究生，主要研究方向模式识别、系统仿真。

金炜东(1959－)，男，西南交通大学电气学院，教授博导，主要研究方向模式识别、系统仿真。E-mail:1044211493@qq.com