基于QPSO的水下加肋圆柱壳体噪声优化设计

刘金实，强学才，商德江，陈鸿洋

（1.哈尔滨工程大学 水声技术重点实验室，哈尔滨 150001；2.哈尔滨工程大学 水声工程学院，哈尔滨 15001；3.中国船舶重工集团公司 第七〇三研究所，哈尔滨 150001；4.中国舰船研究设计中心 船舶振动噪声重点实验室，武汉 430064）

基于QPSO的水下加肋圆柱壳体噪声优化设计

刘金实1,2，强学才3，商德江1,2，陈鸿洋4

（1.哈尔滨工程大学 水声技术重点实验室，哈尔滨 150001；2.哈尔滨工程大学 水声工程学院，哈尔滨 15001；3.中国船舶重工集团公司 第七〇三研究所，哈尔滨 150001；4.中国舰船研究设计中心 船舶振动噪声重点实验室，武汉 430064）

提出了厚度分布沿轴向周期变化的加肋圆柱壳体有限元矩阵的快速导出算法，并结合边界元法对圆柱壳体在水下受力振动与声辐射进行预报。在此基础上，以低频段内总声辐射功率最小为优化目标，采用量子粒子群算法对厚度沿轴向周期分布的加肋圆柱壳体进行优化设计。数值仿真结果表明，该算法对水下加肋圆柱壳体的噪声优化设计分析周期有明显的改善，合理配置圆柱壳体的厚度分布可以有效的改善圆柱壳体在水下的噪声性能。

振动与波；加肋圆柱壳；优化设计；量子粒子群算法；有限元—边界元法

加肋圆柱壳体是潜器中的典型结构，降低其在水下受力振动的辐射噪声对潜艇的隐身性能有着重要的意义。在过去二十年中，国内外学者对加肋圆柱壳体的振动与声辐射机理进行了广泛的研究[1-3]，其预报方法已趋于成熟。然而据作者所知，针对壳体结构参数的噪声优化设计研究仍然开展得较少。经典的结构—声灵敏度方法[4,5]虽然具有收敛迅速、计算量小的优势，但不具有全局搜索能力，容易陷入局部最优；而以遗传算法为代表的启发式算法，虽然具备了全局寻优的能力，但收敛速度较慢，需要进行大量的预报计算。

为了改善预报计算的速度，本文在有限元—边界元法进行噪声预报的基础上，推导壳体厚度与系统方程组间的关系，得到系统方程组的快速导出算法。同时采用收敛性能较好且具有全局寻优能力的量子粒子群算法，以加肋圆柱壳体在低频段内受力振动的平均声辐射功率为目标函数，以壳体的厚度分布作为优化变量，进行了数值仿真。

1 理论基础

1.1 加肋圆柱壳的声辐射预报

圆柱壳采用矩形截面的环肋加强，见图1(a)，壳体厚度在相邻环肋间呈阶梯、周期分布，见图1(b)，其中阴影区域为环肋。

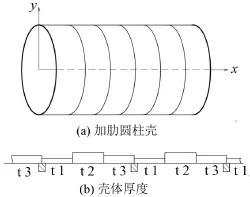
图1 (a)加肋圆柱壳示意图 图1(b)壳体厚度示意图

采用有限元—边界元法计算圆柱壳体受谐和力激励的振动与声辐射问题，其系统方程组为

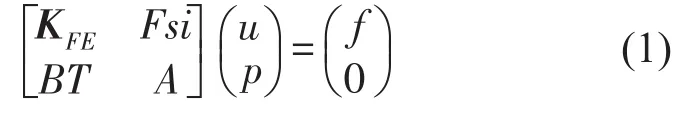
其中KFE为结构广义有限元刚度矩阵，设激励圆频率为ω，结构刚度矩阵为Ks，质量矩阵为Ms，则有

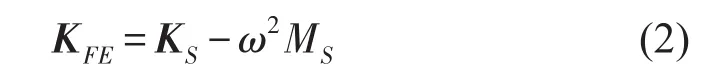
A、B为边界元矩阵，p为结构表面声压分布向量，μ为结构位移向量，T为位移—表面振速转换矩阵，设q为结构表面振速向量，则满足关系

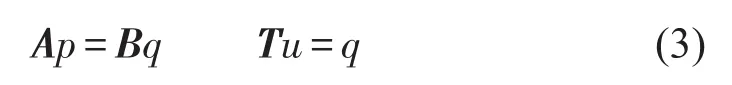
当壳体厚度发生变化，其外形保持不变，而系统矩阵中A、B、T和FSI都只与结构外表面形状有关，因此只需研究KFE与壳体厚度分布的关系。

壳单元的形变可以分为弯曲形变和平面形变两部分。Batoz等人[6]基于离散Kirchhoff理论的四边形单元（DKQ），在避免了引入中间节点的同时符合了应力连续条件，具有良好的收敛性，在对壳体弯曲形变的研究中得到了广泛的应用。而壳体的平面形变可以由经典的膜单元[7]（Mem）进行描述。二者叠加后得出壳单元的刚度矩阵公式

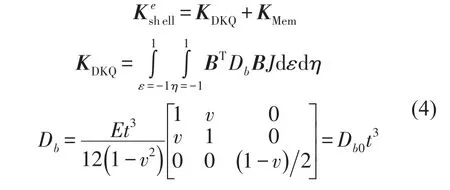
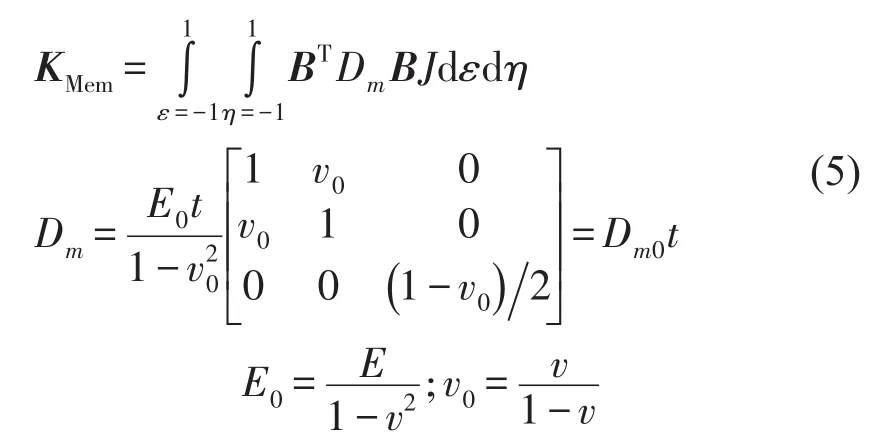
其中Kshelle为壳单元刚度矩阵，KDKQ为DKQ单元刚度矩阵，KMem为膜单元刚度矩阵，t为壳单元厚度，E为杨氏模量，v为泊松比，B为应变矩阵，J为雅克比行列式。引入二维高斯积分，每个维度取3个采样位置即可满足阶次要求[8]，从而得到

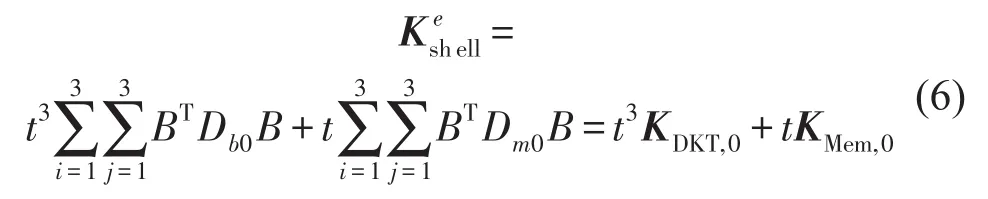
其中KDKT,0和KMem,0分别为与厚度无关的DKQ单元和膜单元刚度矩阵。

根据协调质量模型，壳单元质量矩阵表达式为

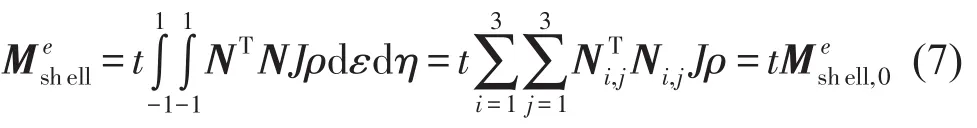
其中ρ为材料密度，N为形函数矩阵。

采用Timoshenko梁单元对圆柱壳内部环肋进行离散化，并将各个单元的刚度、质量矩阵按总体自由度叠加，从而得到结构总体的刚度矩阵和质量矩阵

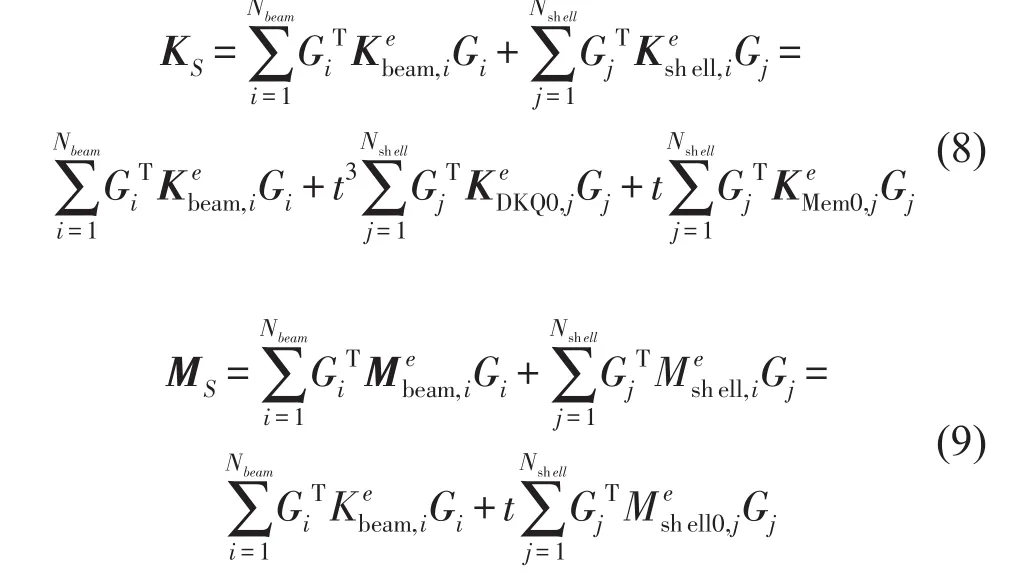
其中Ks和Ms分别为圆柱壳总体刚度和质量矩阵，Kbeam,ie和Mbeam,ie分别为第i个梁单元的刚度和质量矩阵，Kshell,je和Mshell,je分别为第j个壳单元的刚度和质量矩阵，Kshell0,je和Mshell0,je分别为对应单元的厚度无关刚度矩阵和质量矩阵。

本文考虑情况为壳体厚度沿轴向周期变化，设每个周期内有n列单元，则可以合并厚度相同的单元矩阵，设端板和环肋部分各单元集成后得到的部分刚度、质量矩阵分别为Kb、Mb，得到结构刚度矩阵、质量矩阵与厚度分布的关系

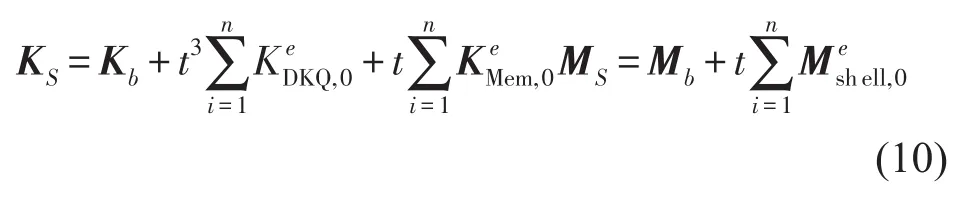
1.2 基于量子粒子群算法的噪声优化

声辐射功率是衡量结构噪声性能的重要指标，它可以由结构表面的声压p和外法向位移u，根据以下公式得出

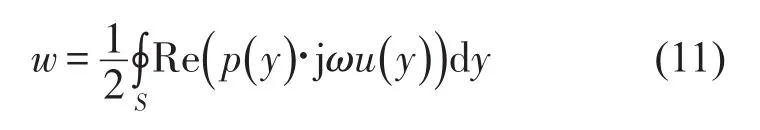
根据以上推导可知，声辐射功率是壳体厚度分布的复杂函数，传统的优化设计方法难易适用。

量子粒子群算法[9]（QPSO）是粒子群算法[10]（PSO）的一种改进，在继承了PSO算法收敛迅速、控制参量少的优点同时，克服了PSO算法搜索空间上的局限，被认为是PSO算法发展的重要进步。QPSO算法的流程图见图2。该算法以一定数量随机产生的初始解作为初始群体，计算各个解的适应函数值，选取适应度最佳的解作为当前全局最优解Gbest，计算当前粒子平均位置C，则粒子群的进化方程为。

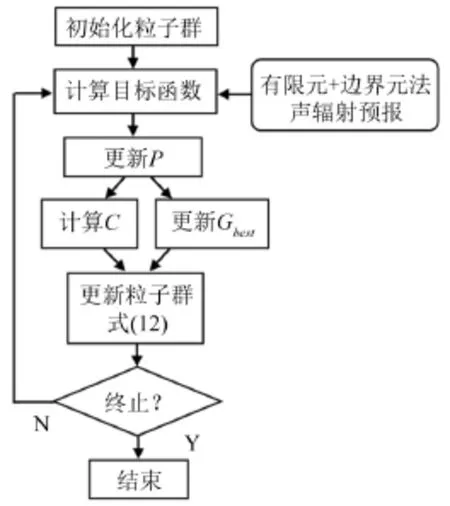
图2 QPSO算法流程图

其中a为收缩—扩张因子，也是该算法运行过程中唯一的控制参量，P为粒子历史最佳位置，f和u为(0，1)区间内的随机数，Xold为粒子当前位置，Xnew为粒子进化后的位置。粒子群每进化一次，相应的需要更新Gbest、P以及C。

要采用QPSO算法对结构的噪声特性进行优化，首先要确定优化的目标函数。针对本文研究模型，目标函数的自变量应为圆柱壳体各列单元的厚度，而因变量应该能够有效的表征结构的噪声性能，可以选取关心的频段内的总辐射声功率，即

其中f为频率。

2 数值计算

2.1 有限元算法验证

首先，为验证本文有限元方法的正确性，分别采用ANSYS软件和自编程序计算圆柱壳模型在真空中受谐和力激励的响应。模型长3 m，半径1 m，环肋间距0.5 m，将壳体沿轴向分为18份，周向24份，网格由648个壳单元、120个梁单元，共650个节点组成；模型二长6 m，半径2 m，环肋间距0.5 m，将壳体沿轴向分为24份，周向32份，网格由1152个壳单元、352个梁单元，共1154个节点组成。两个模型的端板均为10 mm，环肋采用矩形截面的Timoshenko梁，宽6 mm，高8 mm。圆柱壳身厚度均匀，由6 mm逐步变化为11 mm，共51步。两个模型的材料均为钢，密度7 800 kg/m3，泊松比0.3，杨氏模量2.0× 1011N/m。激励力为施加于圆柱壳中心处、幅值1 N的径向谐和力，频率为100 Hz。

图3和图4分别比较了两个模型在激励点处的径向位移响应。从图中可以看出，本文方法解与ANSYS软件解非常接近，方法的正确性得以验证。

图3 模型一位移响应对比图

图4 模型二位移响应对比图

表1比较了模型一、二的分析过程中，形成矩阵、求解等方面的耗时。与每个步骤中所需的矩阵叠加操作相比，分析开始时需要进行的单元矩阵形

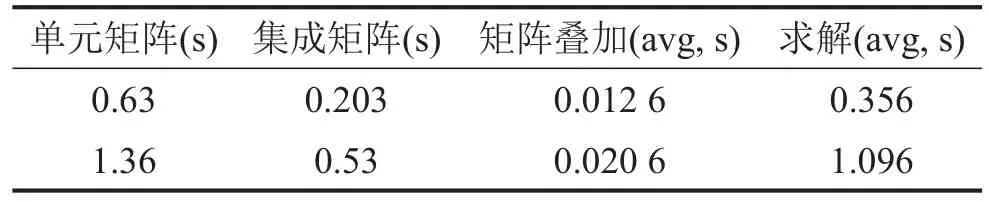
表1 有限元分析耗时统计

成、集成操作要多耗时数十倍。由于引入了单元矩阵的展开项，本文方法中集成操作的计算量较传统方法有所增加，但生成单元矩阵的过程并没有引入额外的运算。综合考虑以上因素发现，有限元矩阵的形成速度得到了显著的提升。

2.2 圆柱壳厚度分布优化

以上节的模型一为研究对象，则相邻两个环肋间，以及环肋与端板间，各有三列壳单元。以三列单元各自的厚度作为优化参量，壳体厚度的取值区间为8 mm～16 mm，为确保优化后的壳体质量没有增加，限定其平均厚度不大于12 mm。

在壳体中心位置处一点施加幅值为1 N的谐和径向激励力。将结构在5 Hz～300 Hz、步长5 Hz的各频点处的总声辐射功率响应作为目标函数的因变量，利用QPSO算法搜索其极小位置，即

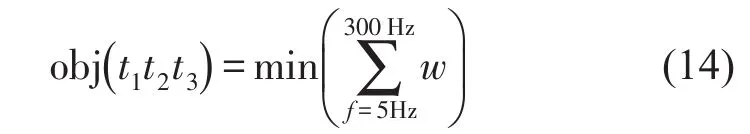
粒子群由50个粒子组成，限定算法的最大迭代次数为100，收缩—扩展因子a的初始值为1，并随着算法的迭代线性递减到0。整个计算过程共需对5 000种不同参数的圆柱壳体进行声辐射预报。根据表1数据估计，本文的有限元算法节约运行时间约69 min。

采用自编程序进行计算，获得三列壳单元的最优厚度分别为11.83 mm，8.47 mm和12.54 mm。图5对比了优化后的设计方案与原始方案（壳身厚度均为12 mm）声辐射功率的频率响应。

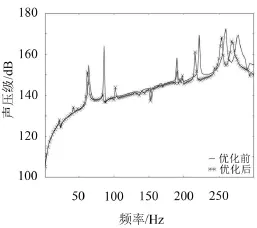
图5 优化前后声辐射功率对比图

由图5可知，优化后的声辐射功率总体上较优化前有所降低。其中86 Hz处的声辐射功率级降低了约21 dB，此外在190 Hz附近、220 Hz附近以及255 Hz附近的峰值也都降低了约5 dB。

3 结语

建立了环肋加强、厚度可变圆柱壳体的参数化有限元模型，提出了圆柱壳体有限元矩阵的快速生成算法，并考虑声学介质与结构的相互作用，结合边界元法对圆柱壳体受谐和力激励的振动与声辐射进行预报；以圆柱壳在低频段内的总声辐射功率为目标函数，采用量子粒子群算法对壳体的厚度分布参数进行优化设计。研究结果表明：

（1）提出的壳体结构有限元矩阵生成算法是正确的，其速度较传统方法具有明显的优势。当启发式优化算法应用于结构的振动与噪声优化时，通常需要对大量不同参数的相似结构进行计算，采用该算法可以显著的节约计算时间，具有一定的工程应用价值；

（2）采取的声辐射预报和声辐射功率优化方法是可行的。通过对环肋加强圆柱壳体的厚度分布进行优化，可在一定程度上降低其在水下的声辐射，改善隐身性能。

[1]何祚镛.水下加环肋圆柱壳体中振动传播[R].哈尔滨：哈尔滨工程大学，1994.

[2]陈美霞，谢坤，魏建辉.带框架肋骨圆柱壳振动特性分析[J].华中科技大学学报(自然科学版)，2014，(3)：127-132.

[3]贺晨，盛美萍，石焕文，等.圆柱壳体振动声辐射效率数值计算分析[J].噪声与振动控制，2006，26(4)：51-54.

[4]刘宝山，赵国忠，王剑.基于设计灵敏度分析的圆柱壳声辐射优化[J].大连理工大学学报，2011，51(3)：313-319.

[5]陈 萍，王敏庆.AutoSEA2声学—结构灵敏度分析软件开发与应用研究[J].噪声与振动控制，2009，29(3)：63-65.

[6]Jean-Louis Batoz,Tahar Mabrouk-Ben.Evaluation of a new quadrilateral thin plate bending element[J].International Journal for Numerical Methods in Engineering, 1982,18(11):1655-1677.

[7]Adnan Ibrahimbegovic,Taylor Robert-L,Wilson Edward-L.A robust quadrilateral membrane finite element with drilling degrees of freedom[J].International Journal for Numerical Methods in Engineering,1990,30(3):445-457.

[8]王勖成.有限单元法[M].北京：清华大学出版社，2003.

[9]JUN Sun,FANG Wei,WU Xiao-jun,et al.Quantum-behaved particle swarm optimization:Analysis of individual particle behavior and parameter selection[J].Evolutionary Computation,2012,20(3):349-393.

[10]James Kennedy.Particle swarm optimization[A].Claude Sammut,Geoffrey I.Webb.Encyclopedia of Machine Learning[C].Springer,2010:760-766.

QPSOAlgorithm-based Noise Optimal Design of Submerged Ring-stiffened Cylindrical Shells

LIU Jin-shi1,2,QIANG Xue-cai3,SHANG De-jiang1,2,CHEN Hong-yang4
(1.Acoustic Science and Technology Laboratory,Harbin Engineering University,Harbin 150001,China; 2.College of UnderwaterAcoustic Engineering,Harbin Engineering University,Harbin 150001,China; 3.CSIC No.703 Research Institute,Harbin 150001,China; 4.National Key Laboratory on Ship Vibration&noise,China Ship Development and Design Center, Wuhan 430064,China)

A fast finite-element matrices generation algorithm was established for analysis of the ring-stiffened cylindrical shells with the thickness varying periodically along the axis.Combining with boundary element method,the underwater vibration and sound radiation of the shells under harmonic force stimulation were predicted.On this basis,the quantum particle swarm algorithm was adopted to minimize the total radiation sound power of the cylindrical shells.Results of the numerical simulation show that this algorithm is effective and economic for noise optimal design of the ring-stiffened underwater cylindrical shells.The optimal design of the thickness distribution can effectively reduce the noise radiation of the shells.

vibration and wave;ring-stiffened cylindrical shell;optimal design;QPSO algorithm;FE-BE method

U661.44

A

10.3969/j.issn.1006-1335.2015.02.003

1006-1355(2015)02-0011-04

2014－08－05

国家自然科学基金（11274080）

刘金实（1984－），男，博士研究生，主要研究方向：水下结构的振动与噪声控制。

商德江，男，教授。E-mail:shangdejiang@hrbeu.edu.cn